बर्नौली वितरण और द्विपद वितरण: क्या अंतर है?

एक यादृच्छिक चर बर्नौली वितरण का अनुसरण करता है यदि इसके केवल दो संभावित परिणाम हैं: 0 या 1।

उदाहरण के लिए, मान लीजिए कि हमने एक सिक्का एक बार उछाला। चलो पी . इसका मतलब यह है कि इसके टेल लैंडिंग की संभावना 1- पी है।

तो, हम लिख सकते हैं:

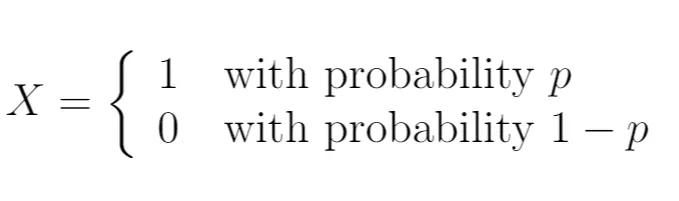
इस मामले में, यादृच्छिक चर X बर्नौली वितरण का अनुसरण करता है। यह केवल दो संभावित मान ले सकता है।

अब, यदि हम एक सिक्के को कई बार उछालते हैं, तो बर्नौली यादृच्छिक चर का योग एक द्विपद वितरण का पालन करेगा।

उदाहरण के लिए, मान लीजिए कि हम एक सिक्के को 5 बार उछालते हैं और k बार चित आने की प्रायिकता जानना चाहते हैं। यह यादृच्छिक चर जैसा दिखता है

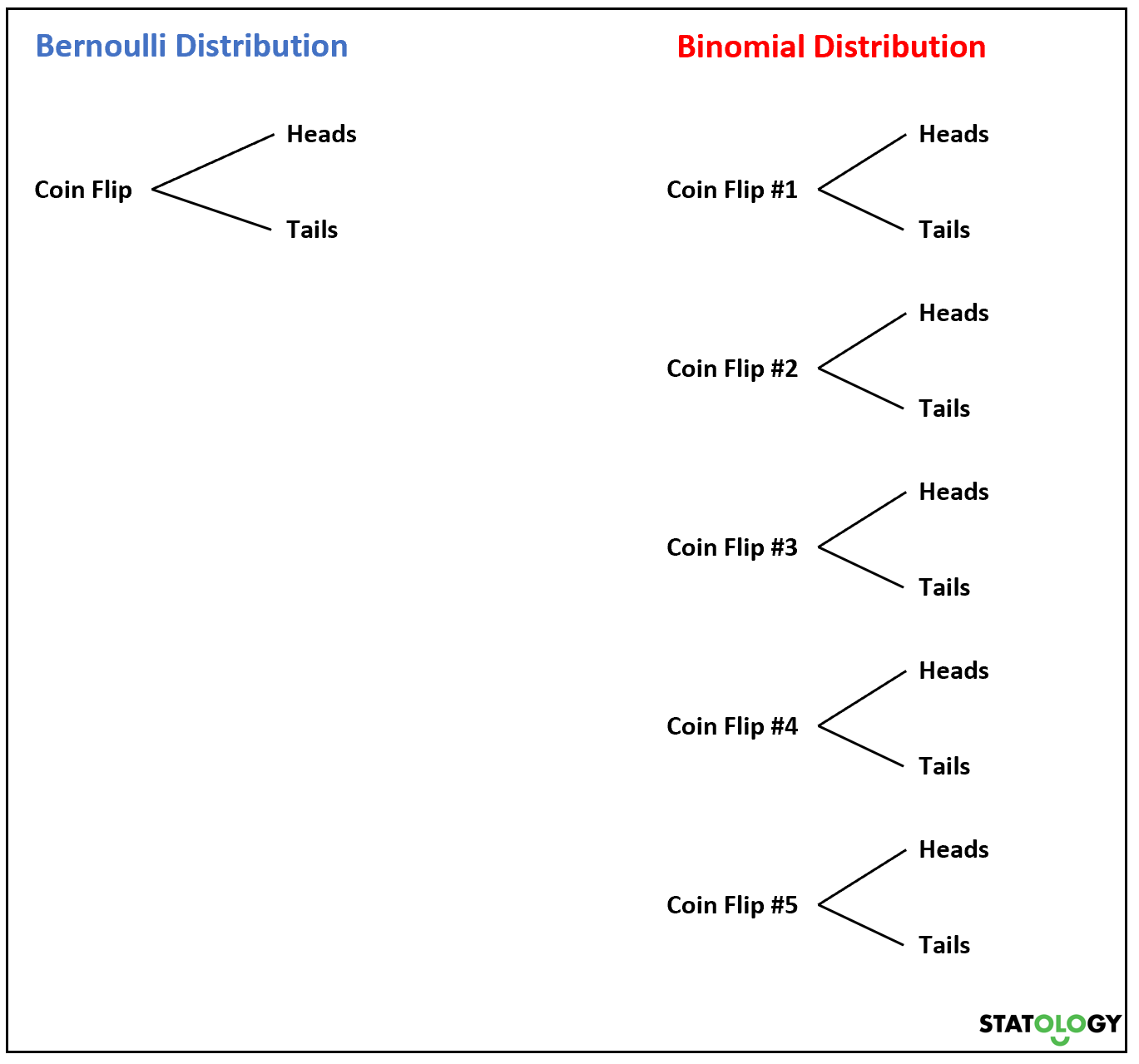
यदि एक यादृच्छिक चर X एक द्विपद वितरण का अनुसरण करता है, तो संभावना है कि X = k की सफलता निम्नलिखित सूत्र द्वारा पाई जा सकती है:

पी(एक्स=के) = _एन सी _के * पी ^के * (1-पी) ^एनके

सोना:

• n: परीक्षणों की संख्या
• k: सफलताओं की संख्या
• पी: किसी दिए गए परीक्षण पर सफलता की संभावना
• _n C _k : n परीक्षणों में k सफलताएँ प्राप्त करने के तरीकों की संख्या

उदाहरण के लिए, मान लीजिए कि हम एक सिक्के को 3 बार उछालते हैं। हम इन 3 फ्लिप के दौरान 0 चित आने की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं:

पी(एक्स=0) = ₃ सी ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

जब n = 1 परीक्षण, द्विपद वितरण बर्नौली वितरण के बराबर होता है।

महत्वपूर्ण लेख

बर्नौली और द्विपद वितरण के संबंध में यहां कुछ महत्वपूर्ण नोट्स दिए गए हैं:

1. एक यादृच्छिक चर जो बर्नौली वितरण का अनुसरण करता है वह केवल दो संभावित मान ले सकता है, लेकिन एक यादृच्छिक चर जो द्विपद वितरण का अनुसरण करता है वह कई मान ले सकता है।

उदाहरण के लिए, एक सिक्के को उछालने पर, हमारे पास या तो 0 या 1 चित होगा। हालाँकि, 5 ड्रा की श्रृंखला में हमारे पास 0, 1, 2, 3, 4 या 5 हेड हो सकते हैं।

2. एक यादृच्छिक चर के लिए द्विपद वितरण का पालन करने के लिए, प्रत्येक बर्नौली परीक्षण में “सफलता” की संभावना बराबर और स्वतंत्र होनी चाहिए।

उदाहरण के लिए, यदि हम “सफलता” को सिर पर उतरने के रूप में परिभाषित करते हैं, तो प्रत्येक टॉस पर सफलता की संभावना 0.5 है और प्रत्येक टॉस स्वतंत्र है – एक टॉस का परिणाम दूसरे के परिणाम को प्रभावित नहीं करता है।

अतिरिक्त संसाधन

द्विपद प्रयोगों का परिचय
द्विपद वितरण का परिचय
द्विपद वितरण के आकार को समझना