बहुपद प्रतिगमन

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 2, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में बहुपद प्रतिगमन क्या है और यह कैसे किया जाता है। इसके अतिरिक्त, आप एक उदाहरण देख पाएंगे जिसमें एक बहुपद प्रतिगमन किया जाता है।

बहुपद प्रतिगमन क्या है?

बहुपद प्रतिगमन , या बहुपद प्रतिगमन , एक प्रतिगमन मॉडल है जिसमें स्वतंत्र चर X और आश्रित चर Y के बीच संबंध को एक बहुपद का उपयोग करके तैयार किया जाता है।

उदाहरण के लिए, द्विघात बहुपद प्रतिगमन मॉडल के लिए समीकरण y=β ₀ +β ₁ x+β ₂ x ² +ε है।

बहुपद प्रतिगमन उन डेटा सेटों को फ़िट करने के लिए उपयोगी है जिनके ग्राफ़ बहुपद वक्र हैं। इसलिए, यदि डेटा नमूने के डॉट प्लॉट में परवलय का आकार है, तो रैखिक प्रतिगमन मॉडल के बजाय द्विघात प्रतिगमन मॉडल का निर्माण करना बेहतर होगा। इस तरह, प्रतिगमन मॉडल समीकरण डेटा नमूने में बेहतर ढंग से फिट होगा।

ध्यान दें कि बहुपद प्रतिगमन एक प्रकार का अरेखीय प्रतिगमन है, ठीक घातीय प्रतिगमन और लघुगणक प्रतिगमन की तरह।

बहुपद प्रतिगमन सूत्र

बहुपद प्रतिगमन मॉडल के लिए समीकरण y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε है।

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

सोना:

$y$

आश्रित चर है.
$x$

स्वतंत्र चर है.
$\beta_0$

बहुपद समाश्रयण समीकरण का स्थिरांक है।
$\beta_i$

चर से जुड़ा प्रतिगमन गुणांक है

$x^i$

.
$\bm{\varepsilon}$

यह त्रुटि या अवशिष्ट है, यानी देखे गए मूल्य और मॉडल द्वारा अनुमानित मूल्य के बीच का अंतर है।

तो अगर हमारे पास कुल मिलाकर एक नमूना है

$n$

अवलोकनों के अनुसार, हम मैट्रिक्स रूप में बहुपद प्रतिगमन मॉडल का प्रस्ताव कर सकते हैं:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

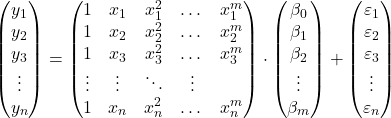
उपरोक्त मैट्रिक्स अभिव्यक्ति को प्रत्येक मैट्रिक्स को एक अक्षर निर्दिष्ट करके फिर से लिखा जा सकता है:

$Y=X\beta+\varepsilon$

इस प्रकार, न्यूनतम वर्ग मानदंड को लागू करके, हम बहुपद प्रतिगमन मॉडल के गुणांक का अनुमान लगाने के सूत्र पर पहुंच सकते हैं:

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

हालाँकि, इन गणनाओं को हाथ से करना बहुत श्रमसाध्य और समय लेने वाला है, इसलिए कंप्यूटर सॉफ़्टवेयर (जैसे मिनीटैब या एक्सेल) का उपयोग करना अधिक सुविधाजनक है जो आपको बहुपद प्रतिगमन मॉडल को बहुत तेज़ी से निष्पादित करने की अनुमति देता है।

बहुपद प्रतिगमन मॉडल का उदाहरण

अब जब हम बहुपद प्रतिगमन की परिभाषा जानते हैं और यह कैसे किया जाता है, तो आइए अवधारणा को पूरी तरह से समझने के लिए एक वास्तविक जीवन का उदाहरण देखें।

सबसे पहले, यह ध्यान में रखा जाना चाहिए कि एक बहुपद प्रतिगमन मॉडल तब निष्पादित किया जाना चाहिए जब डेटा ग्राफ़ में एक बहुपद वक्र का आकार हो। उदाहरण के लिए, यदि डॉटप्लॉट एक घन वक्र के रूप में है, तो हमें एक तृतीय डिग्री बहुपद प्रतिगमन मॉडल बनाने की आवश्यकता है।

तो, जैसा कि आप निम्नलिखित छवि में देखते हैं, हमारे डेटा के डॉट प्लॉट में एक द्विघात आकार होता है, क्योंकि जैसे-जैसे हम स्वतंत्र चर का मान बढ़ाते हैं, आश्रित चर तेजी से बढ़ता है। इस मामले में एक रेखीय प्रतिगमन मॉडल का प्रदर्शन किया गया था और जैसा कि आप देख सकते हैं कि यह बिंदुओं पर अच्छी तरह से फिट नहीं बैठता है क्योंकि इसमें ऐसे अनुभाग हैं जिनमें रेखा सभी बिंदुओं से नीचे है और ऐसे अनुभाग हैं जिनमें रेखा उनके ऊपर है।

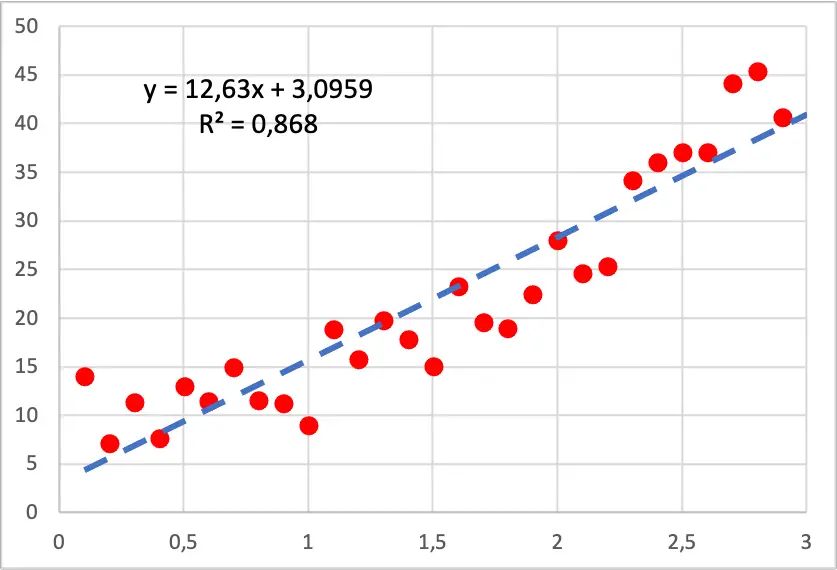
दूसरी ओर, यदि हम एक द्विघात बहुपद प्रतिगमन मॉडल चलाते हैं, तो यह नमूना डेटा को बेहतर ढंग से फिट करता है, जैसा कि आप नीचे दी गई छवि में देख सकते हैं।

इसके अलावा, बहुपद प्रतिगमन मॉडल विकसित करते समय, निर्धारण के गुणांक में काफी सुधार होता है क्योंकि यह 86.80% से 94.05% हो जाता है। इसलिए, नया प्रतिगमन मॉडल डेटासेट को बेहतर ढंग से समझाता है।

दूसरी ओर, एक और संकेत है कि हमें बहुपद प्रतिगमन करने की आवश्यकता है, वह है अवशेषों का आलेखन। यदि एक रेखीय प्रतिगमन में अवशेषों के ग्राफ में एक परवलय या किसी अन्य प्रकार के बहुपद का आकार होता है, तो एक बहुपद प्रतिगमन मॉडल निश्चित रूप से अध्ययन किए गए डेटा को बेहतर ढंग से फिट करता है।

अन्य प्रकार के अरेखीय प्रतिगमन

अरेखीय प्रतिगमन मुख्यतः तीन प्रकार के होते हैं:

बहुपद प्रतिगमन – प्रतिगमन मॉडल समीकरण एक बहुपद के रूप में है।
लघुगणक प्रतिगमन : स्वतंत्र चर का लघुगणक लिया जाता है।
घातीय प्रतिगमन : समीकरण के घातांक में स्वतंत्र चर पाया जाता है।

➤ देखें: लघुगणकीय प्रतिगमन
➤ देखें: घातीय प्रतिगमन

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने