आर में बहुपद प्रतिगमन (चरण दर चरण)

बहुपद प्रतिगमन एक ऐसी तकनीक है जिसका उपयोग हम तब कर सकते हैं जब एक पूर्वसूचक चर और एक प्रतिक्रिया चर के बीच संबंध अरेखीय होता है।

इस प्रकार का प्रतिगमन निम्न रूप लेता है:

वाई = β ₀ ⁺ β ₁ एक्स + β ₂ एक्स ² + … + β _एच

जहाँ h बहुपद की “डिग्री” है।

यह ट्यूटोरियल आर में बहुपद प्रतिगमन कैसे करें इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: डेटा बनाएं

इस उदाहरण के लिए, हम एक डेटासेट बनाएंगे जिसमें 50 छात्रों की कक्षा के लिए अध्ययन किए गए घंटों की संख्या और अंतिम परीक्षा ग्रेड शामिल होगा:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

चरण 2: डेटा को विज़ुअलाइज़ करें

डेटा में एक प्रतिगमन मॉडल फिट करने से पहले, आइए पहले अध्ययन किए गए घंटों और परीक्षा स्कोर के बीच संबंध की कल्पना करने के लिए एक स्कैटरप्लॉट बनाएं:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

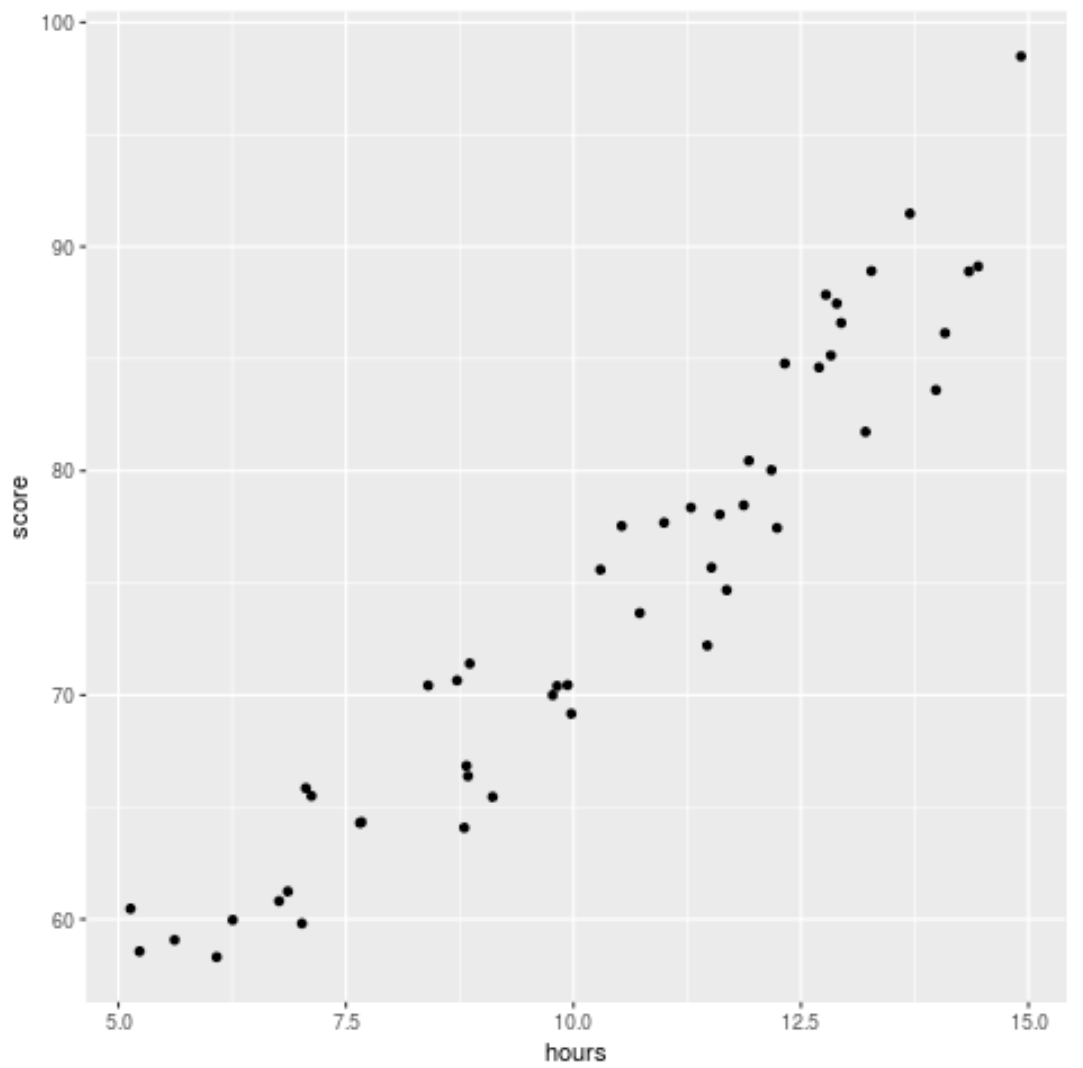
हम देख सकते हैं कि डेटा में थोड़ा द्विघात संबंध है, जो दर्शाता है कि बहुपद प्रतिगमन सरल रैखिक प्रतिगमन की तुलना में डेटा को बेहतर ढंग से फिट कर सकता है।

चरण 3: बहुपद प्रतिगमन मॉडल फ़िट करें

इसके बाद, हम डिग्री h = 1…5 के साथ पांच अलग-अलग बहुपद प्रतिगमन मॉडल फिट करेंगे और प्रत्येक मॉडल के लिए MSE परीक्षण की गणना करने के लिए k = 10 बार के-गुना क्रॉस-सत्यापन का उपयोग करेंगे:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

परिणाम से हम प्रत्येक मॉडल के लिए एमएसई परीक्षण देख सकते हैं:

• डिग्री एच = 1: 9.80 के साथ एमएसई परीक्षण
• डिग्री एच = 2: 8.75 के साथ एमएसई परीक्षण
• डिग्री एच = 3: 9.60 के साथ एमएसई परीक्षण
• डिग्री एच = 4: 10.59 के साथ एमएसई परीक्षण
• डिग्री एच = 5: 13.55 के साथ एमएसई परीक्षण

सबसे कम परीक्षण एमएसई वाला मॉडल डिग्री एच = 2 के साथ बहुपद प्रतिगमन मॉडल बन गया।

यह मूल स्कैटरप्लॉट से हमारे अंतर्ज्ञान से मेल खाता है: एक द्विघात प्रतिगमन मॉडल डेटा के लिए सबसे उपयुक्त है।

चरण 4: अंतिम मॉडल का विश्लेषण करें

अंत में, हम सर्वोत्तम प्रदर्शन करने वाले मॉडल के गुणांक प्राप्त कर सकते हैं:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

परिणाम से, हम देख सकते हैं कि अंतिम फिट मॉडल है:

स्कोर = 54.00526 – 0.07904*(घंटे) + 0.18596*(घंटे) ²

हम इस समीकरण का उपयोग यह अनुमान लगाने के लिए कर सकते हैं कि किसी छात्र को अध्ययन किए गए घंटों की संख्या के आधार पर कितना स्कोर मिलेगा।

उदाहरण के लिए, एक छात्र जो 10 घंटे पढ़ाई करता है उसे 71.81 का ग्रेड मिलना चाहिए:

स्कोर = 54.00526 – 0.07904*(10) + 0.18596*(10) ² = 71.81

हम फिट किए गए मॉडल को यह देखने के लिए भी प्लॉट कर सकते हैं कि यह कच्चे डेटा में कितनी अच्छी तरह फिट बैठता है:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

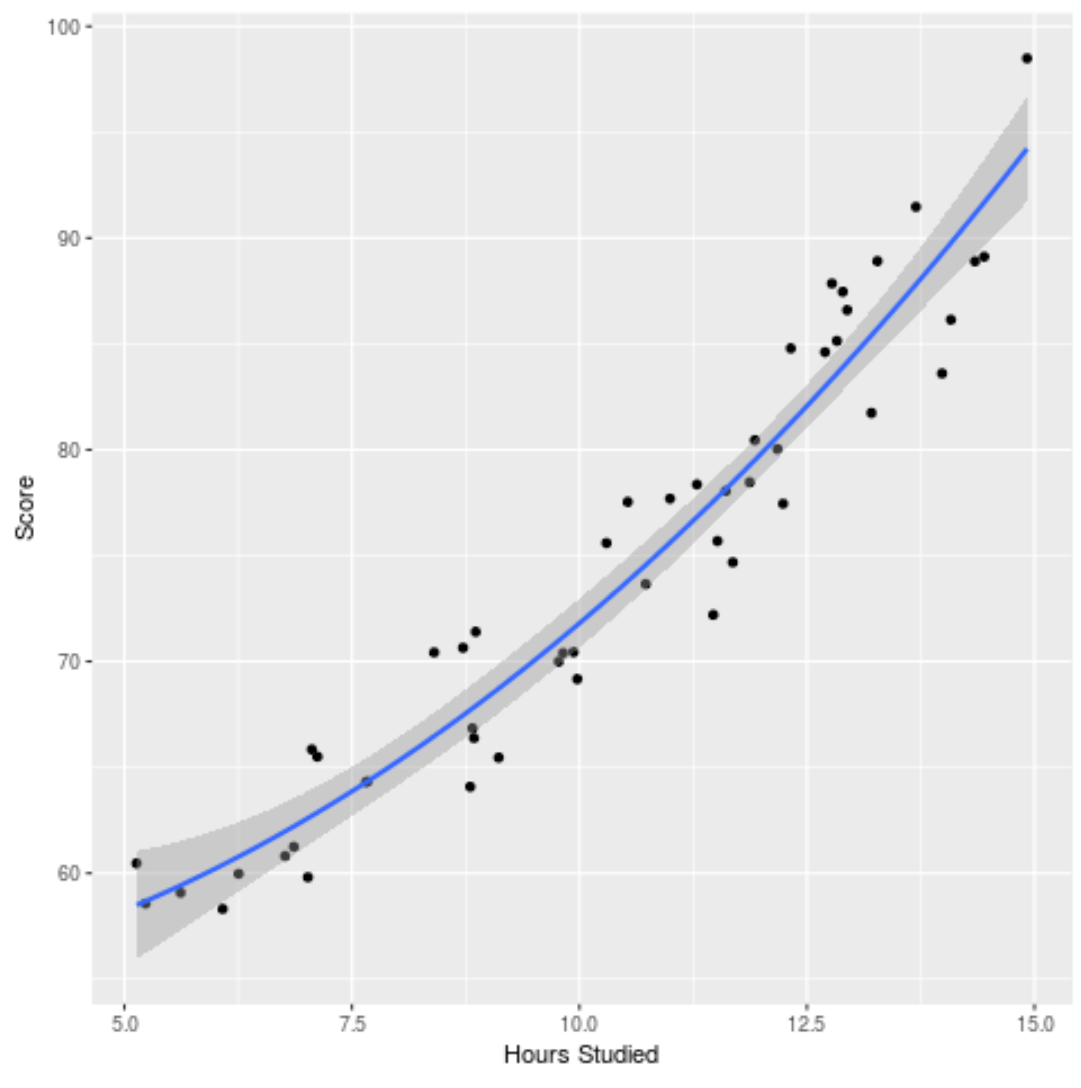
आप इस उदाहरण में प्रयुक्त पूरा आर कोड यहां पा सकते हैं।