एक्सेल में बहुपद प्रतिगमन कैसे करें

प्रतिगमन विश्लेषण का उपयोग एक या अधिक व्याख्यात्मक चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए किया जाता है।

प्रतिगमन विश्लेषण का सबसे आम प्रकार सरल रैखिक प्रतिगमन है, जिसका उपयोग तब किया जाता है जब एक व्याख्यात्मक चर और एक प्रतिक्रिया चर के बीच एक रैखिक संबंध होता है।

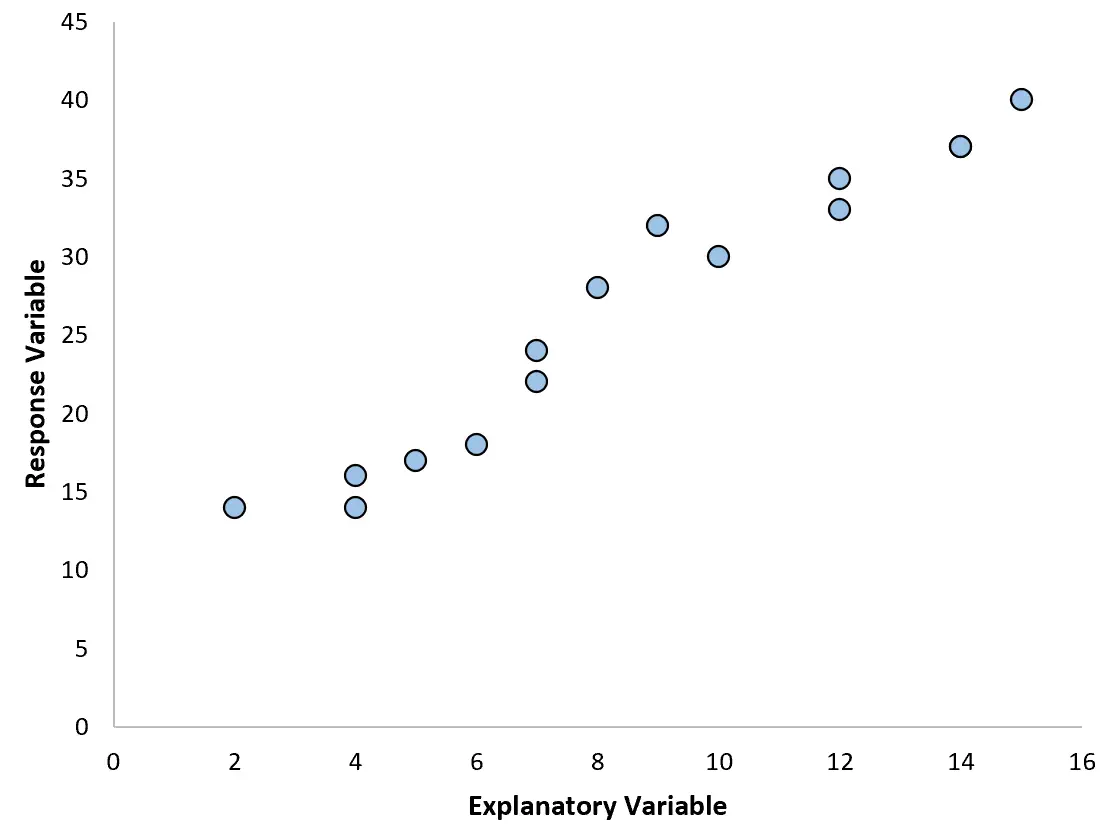
हालाँकि, कभी-कभी एक व्याख्यात्मक चर और एक प्रतिक्रिया चर के बीच का संबंध गैर-रैखिक होता है।

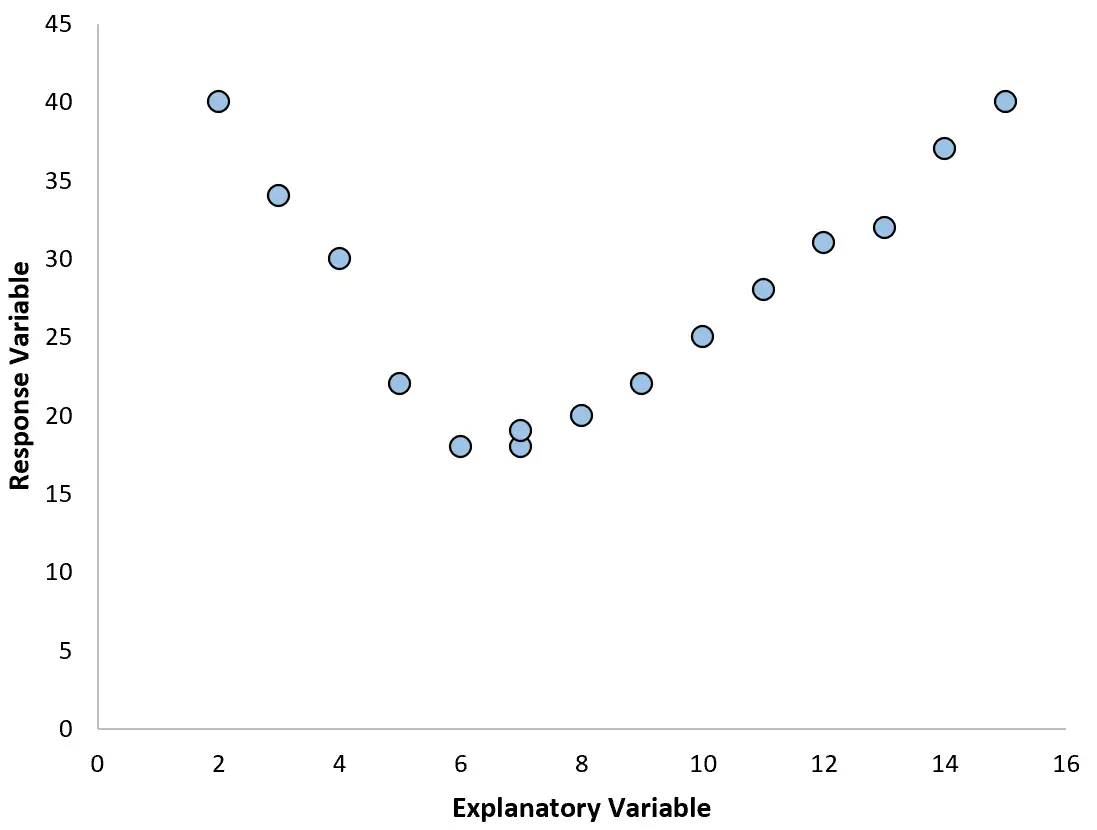
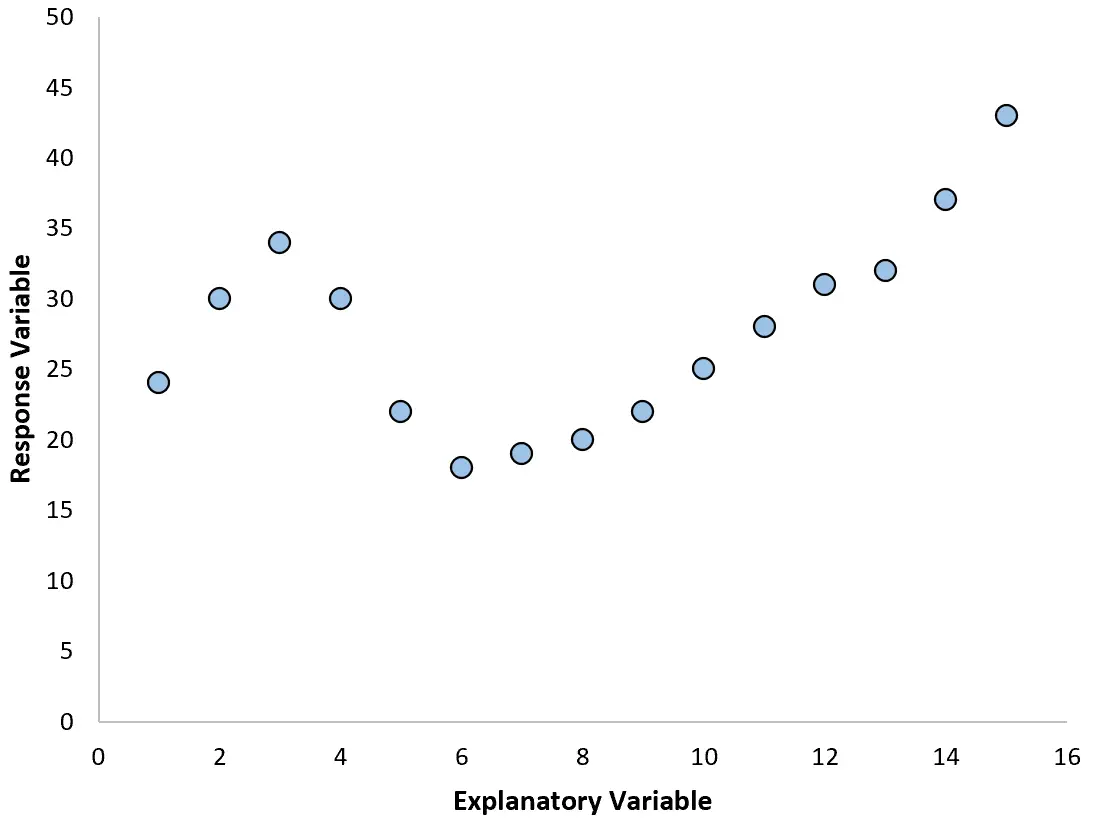
इन मामलों में, बहुपद प्रतिगमन का उपयोग करना समझ में आता है, जो चर के बीच गैर-रेखीय संबंध के लिए जिम्मेदार हो सकता है।

यह ट्यूटोरियल बताता है कि एक्सेल में बहुपद प्रतिगमन कैसे करें।

उदाहरण: एक्सेल में बहुपद प्रतिगमन

मान लीजिए हमारे पास एक्सेल में निम्नलिखित डेटा सेट है:

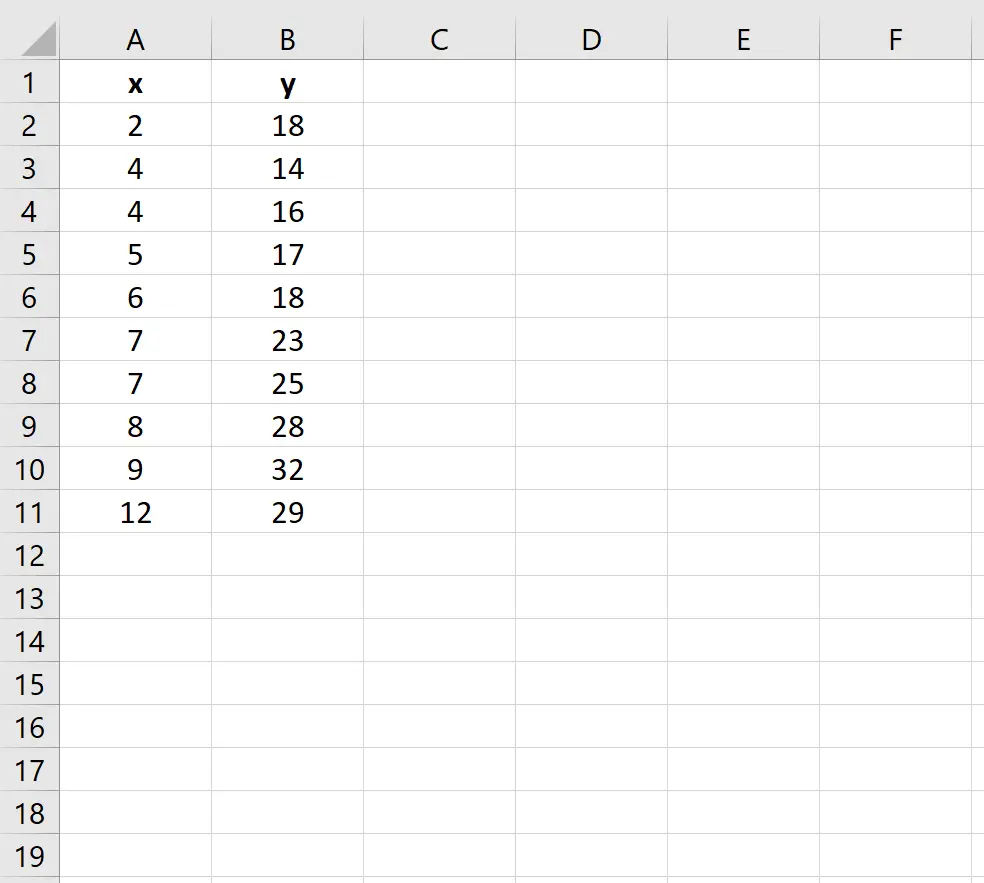
इस डेटा सेट में बहुपद प्रतिगमन समीकरण को फिट करने के लिए निम्नलिखित चरणों को पूरा करें:

चरण 1: एक स्कैटरप्लॉट बनाएं।

सबसे पहले, हमें एक स्कैटरप्लॉट बनाने की आवश्यकता है। इन्सर्ट टैब पर चार्ट समूह में जाएँ और स्कैटर में पहले चार्ट प्रकार पर क्लिक करें:

एक बिंदु बादल स्वचालित रूप से दिखाई देगा:

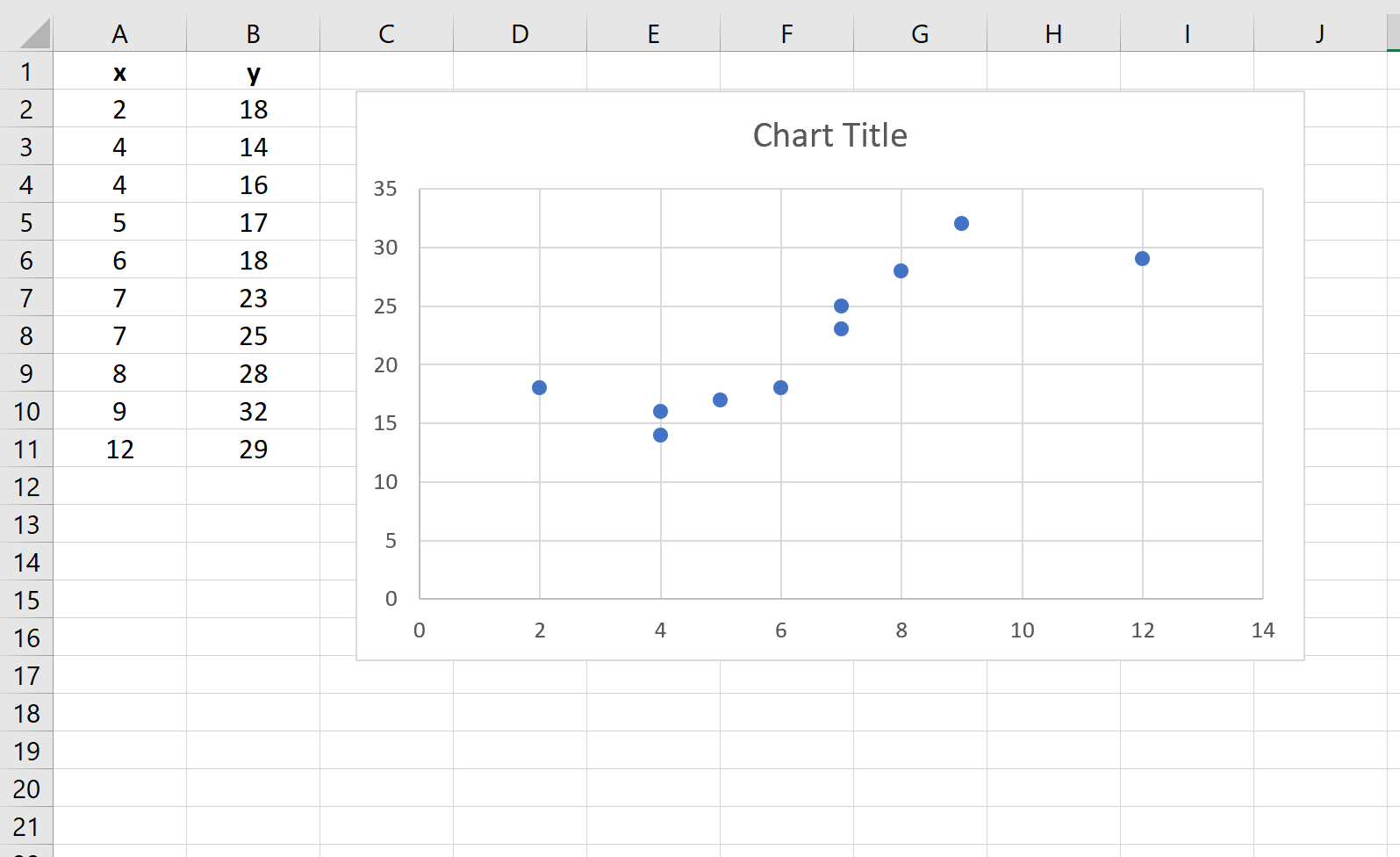
चरण 2: एक ट्रेंड लाइन जोड़ें।

इसके बाद, हमें स्कैटरप्लॉट में एक ट्रेंड लाइन जोड़ने की जरूरत है। ऐसा करने के लिए, पॉइंट क्लाउड में किसी एक बिंदु पर क्लिक करें। इसके बाद, राइट-क्लिक करें और ट्रेंडलाइन जोड़ें चुनें…

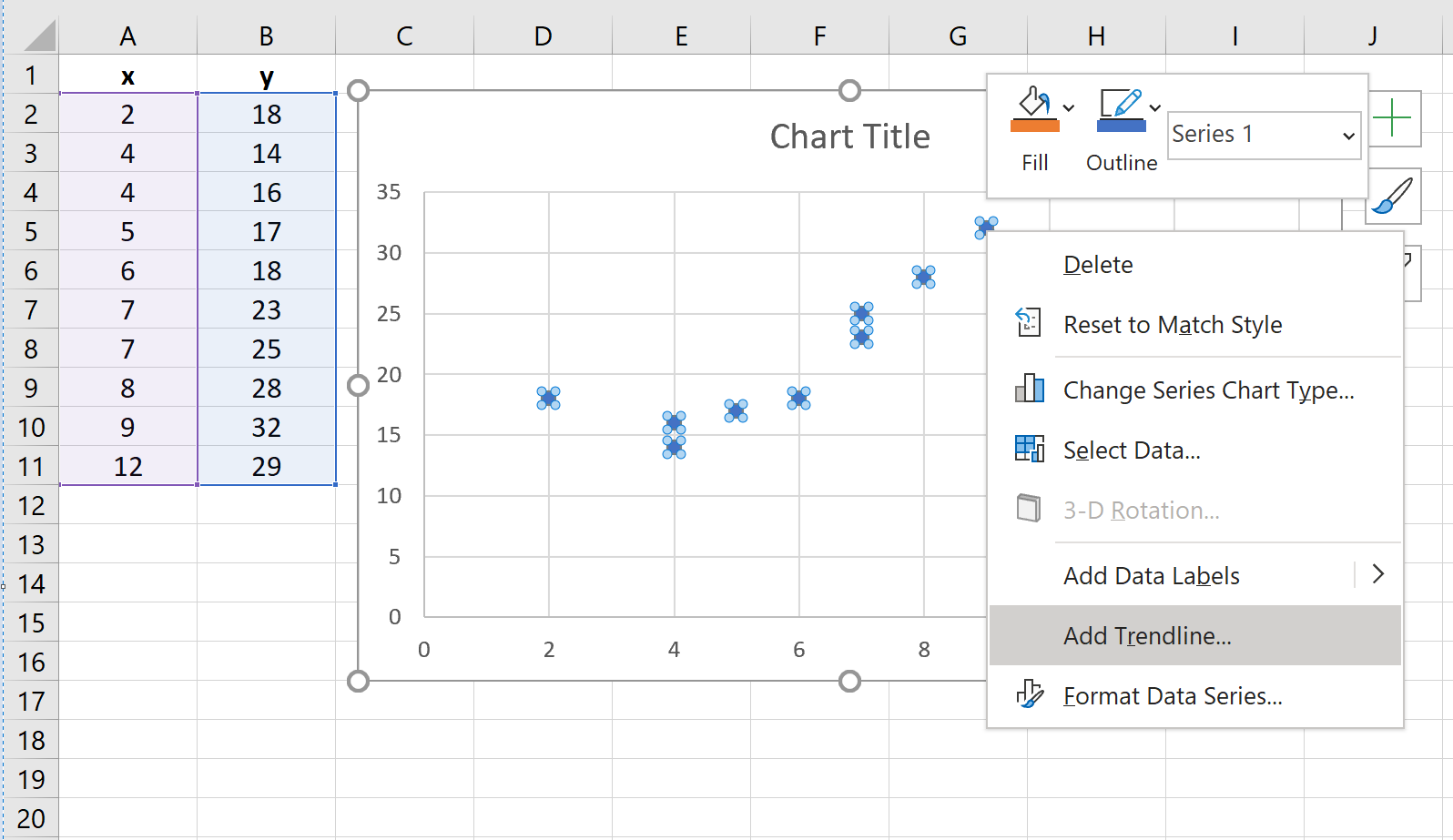
ट्रेंड लाइन निर्दिष्ट करने के विकल्प के साथ एक नई विंडो दिखाई देगी। बहुपद चुनें और वह संख्या चुनें जिसे आप ऑर्डर के लिए उपयोग करना चाहते हैं। हम 3 का उपयोग करेंगे। इसके बाद, नीचे दिए गए बॉक्स को चेक करें जो कहता है कि ग्राफ़ पर समीकरण दिखाएं ।

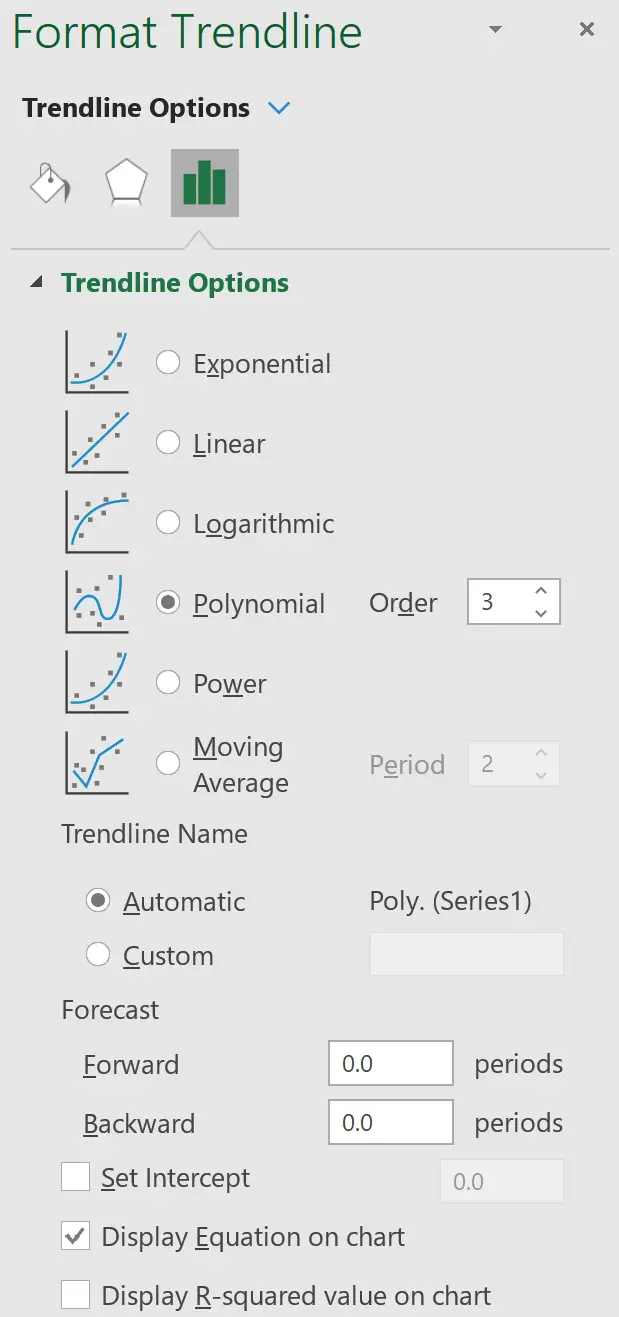
बहुपद प्रतिगमन समीकरण वाली एक प्रवृत्ति रेखा स्वचालित रूप से स्कैटरप्लॉट पर दिखाई देगी:

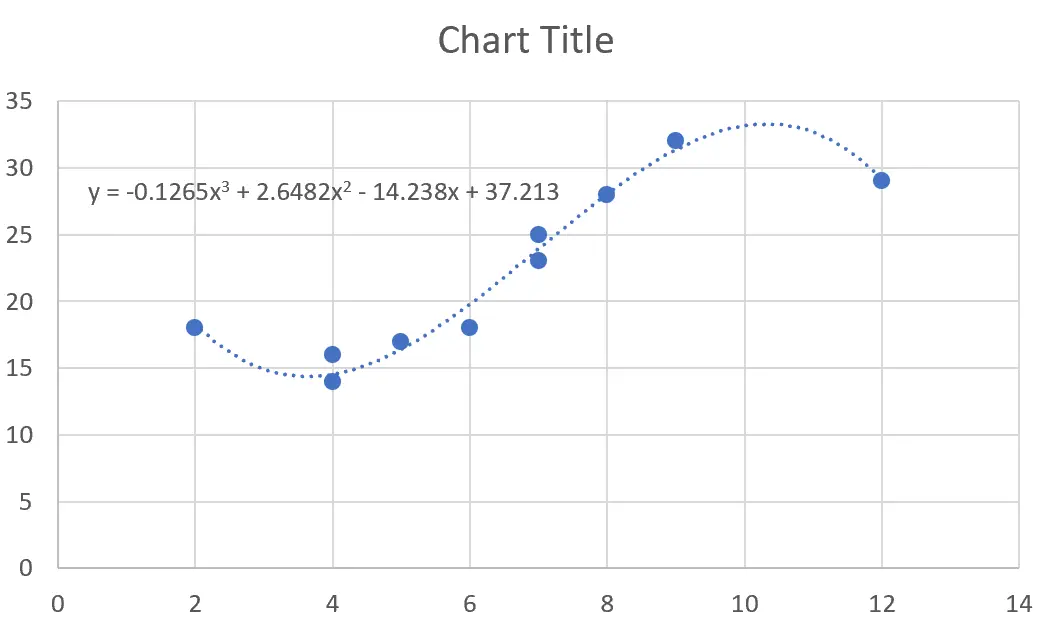
चरण 3: प्रतिगमन समीकरण की व्याख्या करें।

इस विशेष उदाहरण के लिए, हमारा फिट बहुपद प्रतिगमन समीकरण है:

y = -0.1265x ³ + 2.6482x ² – 14.238x + 37.213

इस समीकरण का उपयोग व्याख्यात्मक चर के दिए गए मान को देखते हुए प्रतिक्रिया चर के अपेक्षित मूल्य को खोजने के लिए किया जा सकता है। उदाहरण के लिए, मान लें x = 4. प्रतिक्रिया चर, y के लिए अपेक्षित मान होगा:

y = -0.1265(4) ³ + 2.6482(4) ² – 14.238(4) + 37.213 = 14.5362 ।