बेनफोर्ड का नियम
यह लेख बताता है कि बेनफोर्ड का नियम क्या है। इसके अतिरिक्त, आप यह भी देख पाएंगे कि बेनफोर्ड के नियम की खोज कैसे हुई और इस सांख्यिकीय कानून के अनुप्रयोग क्या हैं।
बेनफोर्ड का नियम क्या है?
बेनफोर्ड का नियम , जिसे पहले अंक का नियम भी कहा जाता है, एक सांख्यिकीय कानून है जो कहता है कि डेटा के एक टुकड़े का पहला अंक 1 होने की संभावना इस संभावना से अधिक है कि यह एक अन्य संख्या है।
दूसरे शब्दों में, बेनफोर्ड का नियम कहता है कि वास्तविक जीवन में मौजूद संख्यात्मक डेटा के एक सेट में, नंबर 1 डेटा के पहले अंक के रूप में सबसे अधिक दोहराया जाने वाला नंबर है।
इसके अतिरिक्त, संख्या जितनी अधिक होगी, उसके पहले स्थान पर आने की संभावना उतनी ही कम होगी। इसलिए, पहली संख्या के 2 की तुलना में 1 होने की अधिक संभावना है, लेकिन 3 की तुलना में 2 की अधिक संभावना है, 4 की तुलना में 3 की अधिक संभावना है, इत्यादि।
बेनफोर्ड के कानून का नाम अमेरिकी फ्रैंक बेनफोर्ड के नाम पर रखा गया है। हालाँकि उन्होंने इसका आविष्कार नहीं किया था, बेनफोर्ड ने इस सांख्यिकीय नियम को लोकप्रिय बनाया। नीचे हम बेनफोर्ड के नियम की उत्पत्ति देखेंगे।
बेनफोर्ड का नियम सूत्र
बेनफोर्ड का नियम कहता है कि पहला अंक एक निश्चित संख्या होने की संभावना उस संख्या पर एक प्लस एक के लघुगणक के बराबर है।
इसलिए बेनफोर्ड के नियम का सूत्र इस प्रकार है:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
इसलिए, बेनफोर्ड के नियम सूत्र से, हम प्रत्येक संख्या के लिए संभावना प्राप्त कर सकते हैं कि यह डेटा आइटम का पहला अंक है। निम्नलिखित तालिका में आप सभी संभावनाओं का प्रतिशत देख सकते हैं:
| आकृति | सम्भावना है कि पहला नंबर हो |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
इसके अतिरिक्त, नीचे आप एक हिस्टोग्राम देख सकते हैं जिसमें बेनफोर्ड के कानून की सभी संभावनाओं को ग्राफिक रूप से दर्शाया गया है:
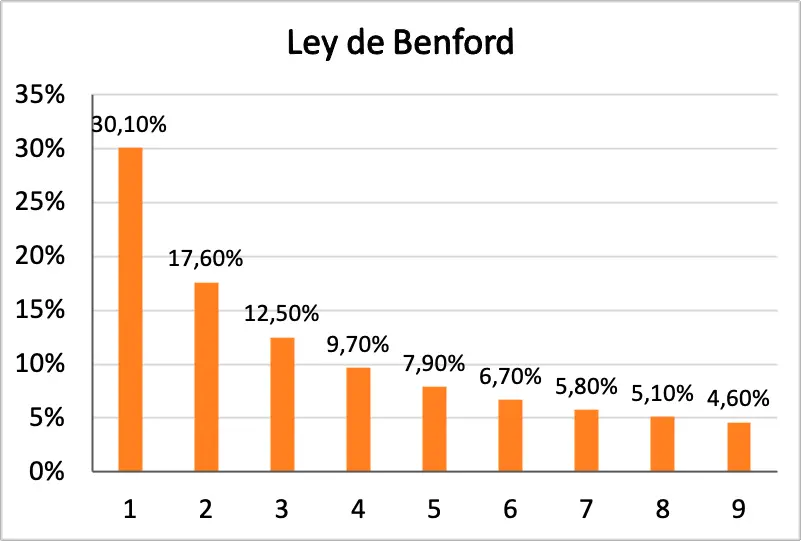
बेनफोर्ड के नियम का इतिहास
1881 में, गणितज्ञ साइमन न्यूकॉम्ब ने बेनफोर्ड का नियम निकाला जब उन्हें पता चला कि लघुगणक तालिकाओं के पहले पृष्ठों का उपयोग अंतिम पृष्ठों की तुलना में काफी अधिक किया गया था। जिसका मतलब था कि संख्याओं के पहले अंक समान रूप से संभावित नहीं हैं, लेकिन 1, 2 से अधिक बार था, 2, 3 से अधिक बार था, और इसी तरह 9 तक।
हालाँकि, न्यूकॉम्ब ने इस बात का कोई सांख्यिकीय प्रमाण नहीं छोड़ा कि इस नियम का पालन किया गया था, उन्होंने बस लघुगणक तालिकाओं की टूट-फूट से कटौती की।
बाद में, विशेष रूप से 1938 में, भौतिक विज्ञानी फ्रैंक बेनफोर्ड ने वही अवलोकन किया और इसे अनुभवजन्य रूप से सत्यापित करने के लिए एक प्रयोग भी किया। 20 अलग-अलग नमूनों से 20,229 मानों के सांख्यिकीय डेटा सेट पर, उन्होंने प्रत्येक डेटा के पहले अंक पर एक अध्ययन किया। इसलिए, परिणामों के आधार पर, उन्होंने प्रदर्शित किया कि बेनफोर्ड का नियम पूरा हो गया है और उस सूत्र को निकाला जिसने उन्हें पहले अंक के एक निश्चित संख्या होने की संभावना की गणना करने की अनुमति दी (हमने इस सूत्र को ऊपर देखा)।
संक्षेप में, हालाँकि बेनफोर्ड का नियम सबसे पहले साइमन न्यूकॉम्ब द्वारा खोजा गया था, लेकिन उसका नाम फ्रैंक बेनफोर्ड के नाम पर रखा गया है क्योंकि वह वही था जिसने इस सांख्यिकीय कानून को सत्यापित किया था।
बेनफोर्ड के नियम के अनुप्रयोग
बेनफोर्ड का नियम एक सांख्यिकीय कानून है जिसका अनुप्रयोग बहुत भिन्न क्षेत्रों में होता है। उदाहरण के लिए, बेनफोर्ड का नियम अर्थशास्त्र, जीव विज्ञान और यहां तक कि राजनीति में भी व्यापक रूप से उपयोग किया जाता है।
अर्थशास्त्र में, बेनफोर्ड के नियम का उपयोग अक्सर डेटा हेरफेर का पता लगाने के लिए किया जाता है, क्योंकि यदि कोई डेटा सेट बेनफोर्ड के कानून के अनुरूप नहीं है, तो यह इंगित करता है कि डेटा में हेरफेर किया गया है। उदाहरण के लिए, इस कानून का उपयोग कर धोखाधड़ी के संभावित मामलों का पता लगाने के लिए किया जाता है।
यह ध्यान दिया जाना चाहिए कि बेनफोर्ड के नियम का उपयोग यादृच्छिक घटनाओं की सच्चाई को प्रदर्शित करने के लिए नहीं किया जाता है, क्योंकि परिणाम समसंभाव्य हैं। इस प्रकार, बेनफोर्ड के नियम का उपयोग लॉटरी परिणामों को सत्यापित करने के लिए नहीं किया जा सकता है।
दूसरी ओर, आनुवंशिकी में, बेनफोर्ड के नियम का उपयोग विभिन्न प्रकार के जीवों के बीच जीनोम की लंबाई में अंतर का विश्लेषण करने के लिए किया जा सकता है।
अंत में, बेनफोर्ड के कानून को लागू करके मतदाता धोखाधड़ी का पता लगाने का भी प्रयास किया गया है, हालांकि इस मामले में इसकी उपयोगिता पर सवाल उठाया गया है।