बेयस प्रमेय

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 1, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि बेयस प्रमेय क्या है और संभाव्यता और सांख्यिकी में इसका उपयोग किस लिए किया जाता है। इस प्रकार, आप जानेंगे कि बेयस प्रमेय का सूत्र क्या है, बेयस प्रमेय के हल किए गए उदाहरण और इस प्रमेय के अनुप्रयोग क्या हैं।

बेयस प्रमेय क्या है?

संभाव्यता सिद्धांत में, बेयस प्रमेय एक कानून है जिसका उपयोग किसी घटना की संभावना की गणना करने के लिए किया जाता है जब उस घटना के बारे में प्राथमिक जानकारी ज्ञात होती है।

अधिक विशेष रूप से, बेयस का प्रमेय गणितीय रूप से घटना बी दिए गए घटना ए की संभावना को बी दिए गए ए की संभावना से जोड़ता है।

उदाहरण के लिए, यदि आप पहले से जानते हैं कि किसी व्यक्ति को फ्लू होने पर सिरदर्द होगा, तो आप इस संभावना को निर्धारित करने के लिए बेयस प्रमेय का उपयोग कर सकते हैं कि किसी व्यक्ति को सिरदर्द होने पर फ्लू होगा।

बेयस प्रमेय के कई अनुप्रयोग हैं, उदाहरण के लिए, इसका उपयोग चिकित्सा, अर्थशास्त्र या प्रौद्योगिकी में अन्य घटनाओं द्वारा वातानुकूलित कुछ घटनाओं की संभावनाओं की गणना करने के लिए किया जाता है। नीचे, हम बेयस प्रमेय के विभिन्न अनुप्रयोगों के बारे में विस्तार से जानेंगे।

बेयस प्रमेय का आविष्कार अंग्रेजी गणितज्ञ थॉमस बेयस (1702-1761) द्वारा किया गया था, हालाँकि इसे मरणोपरांत 1763 में प्रकाशित किया गया था।

➤ देखें: सशर्त संभाव्यता

बेयस प्रमेय का सूत्र

बेयस का प्रमेय कहता है किपारस्परिक रूप से अनन्य घटनाओं {ए ₁ , ए ₂ ,…, ए _आई ,…, ए _एन } के सेट से बना एक नमूना स्थान दिया गया है, जिसकी संभावनाएं शून्य नहीं हैं और एक अन्य घटना बी है, हम गणितीय रूप से सशर्त से संबंधित हो सकते हैं A _i की संभाव्यता घटना B दी गई है और B की सशर्त संभाव्यता A _i दी गई है।

तो, बेयस प्रमेय का सूत्र , जिसे बेयस नियम भी कहा जाता है, है:

सोना:

$P(A_i|B)$

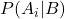
घटना ए की सशर्त संभाव्यता है, _जिसे घटना बी दिया गया है, जिसे पश्च संभाव्यता कहा जाता है।
$P(B|A_i)$

घटना A _i दिए जाने पर घटना B की सशर्त संभाव्यता है।
$P(A_i)$

वह प्रायिकता है कि घटना A _i घटित होगी, जिसे प्राथमिक प्रायिकता कहा जाता है।

ध्यान दें कि बेयस प्रमेय सूत्र का हर घटना बी की कुल संभावना है।

बेयस प्रमेय का उदाहरण

एक बार जब हम बेयस प्रमेय की परिभाषा देखते हैं और इसका सूत्र क्या है, तो हम अवधारणा को बेहतर ढंग से समझने के लिए बेयस प्रमेय के साथ संभाव्यता की गणना कैसे की जाती है इसका एक सुलझा हुआ उदाहरण देखेंगे।

एक इलेक्ट्रॉनिक्स स्टोर तीन ब्रांड के टेलीविजन बेचता है: एक दोषपूर्ण टीवी देखते हुए, इसकी क्या संभावना है कि यह ब्रांड Z टीवी है?

यह अभ्यास हमें संभावनाएं देता है कि एक ग्राहक टेलीविजन के प्रत्येक ब्रांड को खरीदेगा:

घटना A ₁ : एक ग्राहक एक ब्रांड X का टेलीविजन खरीदता है → P(A ₁ )=0.20
घटना A ₂ : एक ग्राहक एक ब्रांड Y टेलीविजन खरीदता है → P(A ₂ )=0.50
घटना A ₃ : एक ग्राहक एक ब्रांड Z टेलीविजन खरीदता है → P(A ₃ )=0.30

इसके अलावा, रीडिंग से हमें यह संभावना भी मिलती है कि प्रत्येक ब्रांड का टेलीविजन ख़राब है:

इवेंट बी: टीवी ख़राब है

बी|ए ₁ : एक ब्रांड एक्स टेलीविजन दिया गया है, टेलीविजन दोषपूर्ण है → पी(बी|ए ₁ )=0.05
बी|ए ₂ : एक ब्रांड वाई टेलीविजन दिया गया है, टेलीविजन दोषपूर्ण है → पी(बी|ए ₂ )=0.03
बी|ए ₃ : एक ब्रांड जेड टेलीविजन दिया गया है, टेलीविजन दोषपूर्ण है → पी(बी|ए ₃ )=0.04

तो हमारी रुचि की सभी घटनाओं का संभाव्यता वृक्ष इस प्रकार है:

इसलिए, इस संभावना की गणना करने के लिए कि, एक दोषपूर्ण टेलीविजन दिया गया है, यह ब्रांड Z है, हमें बेयस प्रमेय से सूत्र का उपयोग करना चाहिए:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

इस उदाहरण में प्रयुक्त शब्दावली का उपयोग करते हुए, बेयस का सूत्र इस तरह दिखता है:

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

इस प्रकार, किसी दिए गए दोषपूर्ण टेलीविजन के ब्रांड Z होने की प्रायिकता की गणना इस प्रकार है:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}$

निष्कर्षतः, संभावना है कि यदि कोई टेलीविजन ख़राब है, तो वह ब्रांड Z है, 32% है।

बेयस प्रमेय के अनुप्रयोग

बेयस प्रमेय के कई अनुप्रयोग हैं, जिनमें शामिल हैं:

मेडिकल परीक्षण : डायग्नोस्टिक परीक्षण पास करने की संभावना निर्धारित करने के लिए बेयस प्रमेय का उपयोग चिकित्सा में अक्सर किया जाता है। उदाहरण के लिए, एचआईवी परीक्षण के मामले में, यदि परीक्षण का परिणाम सकारात्मक है तो प्रमेय का उपयोग इस संभावना की गणना करने के लिए किया जा सकता है कि किसी व्यक्ति में वास्तव में वायरस है।
वित्तीय विश्लेषण : वित्त में, बेयस प्रमेय का उपयोग इस संभावना की गणना करने के लिए किया जाता है कि कुछ आर्थिक घटनाएं, जैसे स्टॉक मूल्य में वृद्धि या कमी, आर्थिक चर का एक सेट दिए जाने पर घटित होंगी।
बाज़ार अनुसंधान : बेयस प्रमेय यह निर्धारित करना संभव बनाता है, उदाहरण के लिए, इस उत्पाद का विज्ञापन देखने के बाद कोई व्यक्ति उत्पाद खरीदेगा इसकी संभावना।
मौसम का पूर्वानुमान : मौसम मॉडल भी बेयस प्रमेय का उपयोग यह निर्धारित करने के लिए करते हैं कि देखे गए डेटा के आधार पर दिया गया मौसम पूर्वानुमान सच होगा। इससे जलवायु पूर्वानुमानों की सटीकता में सुधार होता है।
कंप्यूटर सुरक्षा – साइबर सुरक्षा में, बेयस प्रमेय को इस संभावना को निर्धारित करने के लिए लागू किया जा सकता है कि एक संदिग्ध गतिविधि वास्तव में कंप्यूटर सिस्टम पर हमला है।

बेयस प्रमेय समस्याएँ हल की गईं

अभ्यास 1

ऐसा अनुमान है कि 1% जनसंख्या किसी न किसी बीमारी से पीड़ित है। इस बीमारी का पता लगाने के लिए एक परीक्षण सकारात्मक मामलों के लिए 95% सटीक और नकारात्मक मामलों के लिए 90% सटीक है। यदि यादृच्छिक रूप से चुना गया कोई व्यक्ति सकारात्मक परीक्षण करता है, तो इसकी क्या संभावना है कि उसे वास्तव में यह बीमारी है?

समाधान देखें

अभ्यास कथन हमें निम्नलिखित संभावनाएँ देता है:

A ₁ : व्यक्ति को यह बीमारी है → P(A ₁ )=0.01
ए ₂ : व्यक्ति को यह बीमारी नहीं है → पी(ए ₂ )=0.99

बी: परीक्षण सकारात्मक है
बी|ए ₁ : जब व्यक्ति को यह बीमारी हो तो परीक्षण सकारात्मक होता है → पी(बी|ए ₁ )=0.95
बी|ए ₂ : परीक्षण तब सकारात्मक होता है जब व्यक्ति को यह बीमारी नहीं होती है → पी(बी|ए ₂ )=1-0.90=0.10

फिर, इस संभावना की गणना करने के लिए कि यादृच्छिक रूप से चुने गए व्यक्ति को वास्तव में बीमारी है जब सकारात्मक परीक्षण किया जाता है, तो बेयस नियम लागू किया जाना चाहिए:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}$

इसलिए हम मानों को सूत्र में प्रतिस्थापित करते हैं और संभाव्यता गणना करते हैं:

$\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}$

संक्षेप में, यह संभावना कि यादृच्छिक रूप से चुना गया व्यक्ति सकारात्मक परीक्षण करता है और वास्तव में उसे बीमारी है, 8.76% है।

व्यायाम 2

यह अनुमान लगाया गया है कि किसी शेयर के एक दिन में बढ़ने की संभावना 40% है, इसके स्थिर रहने की संभावना 10% है, और इसके गिरने की संभावना 50% है। इसके अलावा, हम जानते हैं कि जब बाजार बढ़ता है, तो 90% संभावना है कि एक वित्तीय विश्लेषक इसकी सही भविष्यवाणी करेगा, कि जब बाजार स्थिर रहता है, तो भविष्यवाणी सही होगी इसकी संभावना 75% है और गिरावट की स्थिति में, संभावना है कि भविष्यवाणी सही होगी। सही भविष्यवाणी की संभावना 75% है। 85%%। यदि कोई विश्लेषक भविष्यवाणी करता है कि बाज़ार गिरेगा, तो इसकी कितनी संभावना है कि यह वास्तव में गिरेगा?

समाधान देखें

इस मामले में, अभ्यास विवरण हमें निम्नलिखित संभावनाएँ प्रदान करता है:

ए ₁ : बाजार एक दिन में बढ़ता है → पी(ए ₁ )=0.40
ए ₂ : बाजार एक दिन में स्थिर रहता है → पी(ए ₂ )=0.10
ए ₃ : बाजार एक दिन में बढ़ता है → पी(ए ₃ )=0.50

बी: विश्लेषक भविष्यवाणी करते हैं कि बाजार गिर जाएगा
बी|ए ₁ : विश्लेषक ने सही भविष्यवाणी की है कि बाजार में वृद्धि होगी → पी(बी|ए ₁ )=0.90
बी|ए ₂ : विश्लेषक ने सही भविष्यवाणी की है कि बाजार स्थिर रहेगा → पी(बी|ए ₂ )=0.75
बी|ए ₃ : विश्लेषक सही भविष्यवाणी करता है कि बाजार गिर जाएगा → पी(बी|ए ₃ )=0.85

इस संभावना को निर्धारित करने के लिए कि एक विश्लेषक भविष्यवाणी करता है कि बाजार गिर जाएगा और वह सही है, हमें बेयस प्रमेय सूत्र का उपयोग करने की आवश्यकता है:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

हम संभाव्यता मानों को बेयस सूत्र में प्रतिस्थापित करते हैं और संभाव्यता की गणना करते हैं:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}$

इसलिए, संभावना है कि एक विश्लेषक सही है जब वे कहते हैं कि शेयर बाजार गिर जाएगा 49.42% है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

बेयस प्रमेय क्या है?

बेयस प्रमेय का सूत्र

बेयस प्रमेय का उदाहरण

बेयस प्रमेय के अनुप्रयोग

बेयस प्रमेय समस्याएँ हल की गईं

अभ्यास 1

व्यायाम 2

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने