पॉइसन वितरण का परिचय

पॉइसन वितरण आंकड़ों में सबसे लोकप्रिय वितरणों में से एक है।

पॉइसन वितरण को समझने के लिए, पहले पॉइसन प्रयोगों को समझना सहायक होता है।

मछली के प्रयोग

पॉइसन प्रयोग एक ऐसा प्रयोग है जिसमें निम्नलिखित गुण होते हैं:

• प्रयोग की सफलताओं की संख्या गिनी जा सकती है।
• किसी विशिष्ट समय (या स्थान) अंतराल के दौरान हुई सफलताओं की औसत संख्या ज्ञात होती है।
• प्रत्येक परिणाम स्वतंत्र है.
• सफलता घटित होने की संभावना अंतराल के आकार के समानुपाती होती है।

पॉइसन प्रयोग का एक उदाहरण किसी दिए गए अस्पताल में प्रति घंटे जन्मों की संख्या है। उदाहरण के लिए, मान लीजिए कि किसी विशेष अस्पताल में प्रति घंटे औसतन 10 जन्म होते हैं। यह एक पॉइसन प्रयोग है क्योंकि इसमें निम्नलिखित चार गुण हैं:

• प्रयोग की सफलताओं की संख्या गिनी जा सकती है – हम जन्मों की संख्या गिन सकते हैं।
• एक विशिष्ट समय अंतराल के दौरान होने वाले जन्मों की औसत संख्या ज्ञात होती है – यह ज्ञात होता है कि प्रति घंटे औसतन 10 जन्म होते हैं।
• प्रत्येक परिणाम स्वतंत्र है – यह संभावना कि एक माँ एक निश्चित घंटे में जन्म देगी, इस संभावना से स्वतंत्र है कि दूसरी माँ जन्म देगी।
• सफल होने की संभावना अंतराल के आकार के समानुपाती होती है: समय अंतराल जितना लंबा होगा, जन्म होने की संभावना उतनी ही अधिक होगी।

हम इस पॉइसन प्रयोग के बारे में संभावनाओं के बारे में सवालों के जवाब देने के लिए पॉइसन वितरण का उपयोग कर सकते हैं जैसे:

• इसकी क्या प्रायिकता है कि एक निश्चित घंटे में 12 से अधिक जन्म होंगे?
• इसकी क्या प्रायिकता है कि एक दिए गए घंटे में 5 से कम जन्म होंगे?
• इसकी क्या प्रायिकता है कि एक निश्चित घंटे में 8 से 11 जन्म होंगे?

मछली वितरण

पॉइसन वितरण एक निश्चित समय अंतराल के दौरान k सफलताएँ प्राप्त करने की संभावना का वर्णन करता है।

यदि एक यादृच्छिक चर

पी(एक्स=के) = λ ^के * ई ^{– λ} / के!

सोना:

• λ: एक विशिष्ट अंतराल के दौरान होने वाली सफलताओं की औसत संख्या
• k: सफलताओं की संख्या
• ई: लगभग 2.71828 के बराबर एक स्थिरांक

उदाहरण के लिए, मान लीजिए कि किसी विशेष अस्पताल में प्रति घंटे औसतन 2 जन्म होते हैं। हम 0, 1, 2, 3 जन्म आदि का अनुभव करने की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं। किसी दिए गए घंटे में:

पी(एक्स=0) = 2 ⁰ * ई ^{– 2} / 0! = 0.1353

पी(एक्स=1) = 2 ¹ * ई ^{– 2/1} ! = 0.2707

पी(एक्स=2) = 2 ² * ई ^{– 2/2} ! = 0.2707

पी(एक्स=3) = 2 ³ * ई ^-2 /3! = 0.1805

हम अनंत तक किसी भी संख्या में जन्म की संभावना की गणना कर सकते हैं। फिर हम इस संभाव्यता वितरण की कल्पना करने के लिए एक सरल हिस्टोग्राम बनाते हैं:

संचयी पॉइसन संभावनाओं की गणना

उपरोक्त सूत्र का उपयोग करके एकल पॉइसन संभाव्यता (उदाहरण के लिए एक अस्पताल में एक दिए गए घंटे में 3 जन्मों का अनुभव होने की संभावना) की गणना करना सरल है, लेकिन संचयी पॉइसन संभावनाओं की गणना करने के लिए हमें व्यक्तिगत संभावनाओं को जोड़ने की आवश्यकता है।

उदाहरण के लिए, मान लें कि हम इस संभावना को जानना चाहते हैं कि अस्पताल में किसी दिए गए घंटे में 1 या उससे कम जन्म होंगे। इस संभाव्यता की गणना के लिए हम निम्नलिखित सूत्र का उपयोग करेंगे:

पी(एक्स≤1) = पी(एक्स=0) + पी(एक्स=1) = 0.1353 + 0.2707 = 0.406

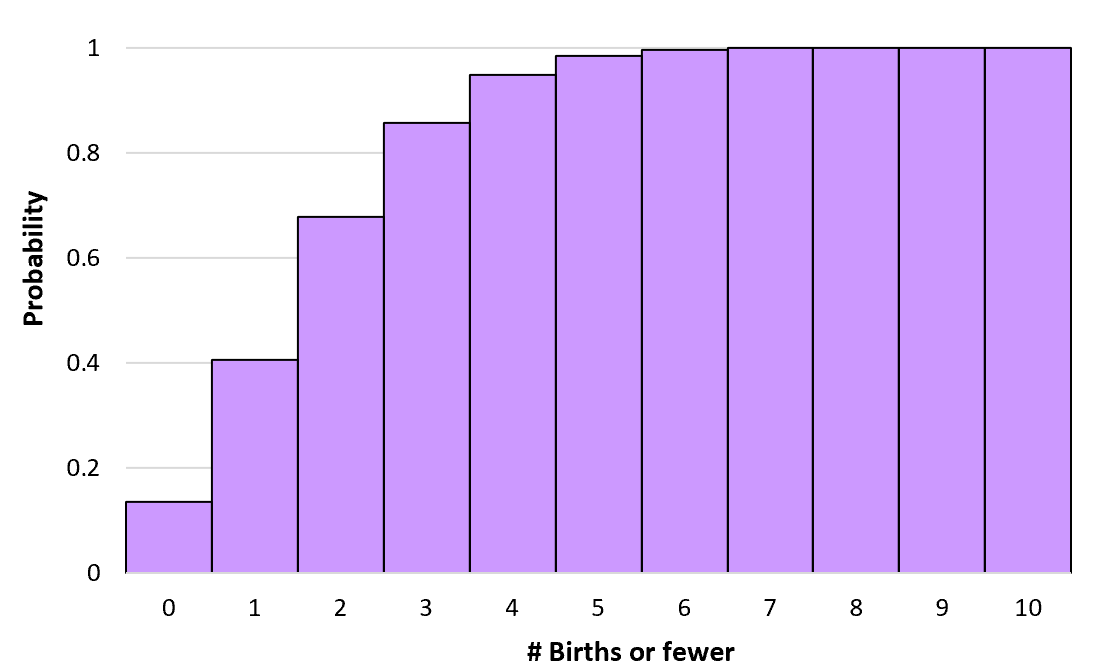
इसे संचयी संभाव्यता कहा जाता है क्योंकि इसमें कई संभावनाओं को जोड़ना शामिल है। हम एक समान सूत्र का उपयोग करके किसी दिए गए घंटे में k या उससे कम जन्मों का अनुभव करने की संचयी संभावना की गणना कर सकते हैं:

P(X≤0) = P(X=0) = 0.1353

पी(एक्स≤1) = पी(एक्स=0) + पी(एक्स=1) = 0.1353 + 0.2707 = 0.406

पी(एक्स≤2) = पी(एक्स=0) + पी(एक्स=1) + पी(एक्स=2) =0.1353 + 0.2707 + 0.2707 = 0.6767

हम अनंत तक किसी भी जन्म के लिए इन संचयी संभावनाओं की गणना कर सकते हैं। फिर हम इस संचयी संभाव्यता वितरण को देखने के लिए एक हिस्टोग्राम बना सकते हैं:

पॉइसन वितरण के गुण

पॉइसन वितरण में निम्नलिखित गुण हैं:

वितरण का माध्य λ है।

वितरण का विचरण भी λ है।

वितरण का मानक विचलन √ λ है।

उदाहरण के लिए, मान लीजिए कि किसी अस्पताल में प्रति घंटे औसतन 2 जन्म होते हैं।

किसी दिए गए घंटे में अपेक्षित जन्मों की औसत संख्या λ = 2 जन्म है।

हमारे द्वारा अपेक्षित जन्मों की संख्या में भिन्नता λ = 2 जन्म है।

मछली वितरण अभ्यास की समस्याएं

पॉइसन वितरण के बारे में अपने ज्ञान का परीक्षण करने के लिए निम्नलिखित अभ्यास समस्याओं का उपयोग करें।

नोट: हम इन प्रश्नों के उत्तर की गणना के लिए पॉइसन वितरण कैलकुलेटर का उपयोग करेंगे।

समस्या 1

प्रश्न: हम जानते हैं कि एक निश्चित वेबसाइट प्रति घंटे 10 बिक्री करती है। किसी दिए गए घंटे में, इसकी क्या प्रायिकता है कि साइट ठीक 8 बिक्री करेगी?

उत्तर: λ = 10 और x = 8 के साथ पॉइसन वितरण कैलकुलेटर का उपयोग करके, हम पाते हैं कि P(X=8) = 0.1126 ।

समस्या 2

प्रश्न: हम जानते हैं कि एक निश्चित रियल एस्टेट एजेंट प्रति माह औसतन 5 बिक्री करता है। किसी दिए गए महीने में, इसकी क्या प्रायिकता है कि वह 7 से अधिक बिक्री करेगी?

उत्तर: λ = 5 और x = 7 के साथ पॉइसन वितरण कैलकुलेटर का उपयोग करके, हम पाते हैं कि P(X>7) = 0.13337 ।

समस्या 3

प्रश्न: हम जानते हैं कि एक निश्चित अस्पताल में प्रति घंटे 4 प्रसव होते हैं। किसी दिए गए घंटे में, क्या संभावना है कि 4 या उससे कम जन्म होंगे?

उत्तर: λ = 4 और x = 4 के साथ पॉइसन वितरण कैलकुलेटर का उपयोग करके, हम पाते हैं कि P(X≤4) = 0.62884 ।

अतिरिक्त संसाधन

निम्नलिखित लेख बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर में पॉइसन वितरण का उपयोग कैसे करें:

आर में पॉइसन वितरण का उपयोग कैसे करें
एक्सेल में पॉइसन वितरण का उपयोग कैसे करें
TI-84 कैलकुलेटर पर पॉइसन संभावनाओं की गणना कैसे करें
पॉइसन वितरण के वास्तविक दुनिया के उदाहरण
मछली वितरण कैलकुलेटर