संपूर्ण गाइड: manova मान्यताओं की जाँच कैसे करें

एक MANOVA (विचरण का बहुभिन्नरूपी विश्लेषण) का उपयोग यह विश्लेषण करने के लिए किया जाता है कि एक या अधिक कारक चर कई प्रतिक्रिया चर को कैसे प्रभावित करते हैं।

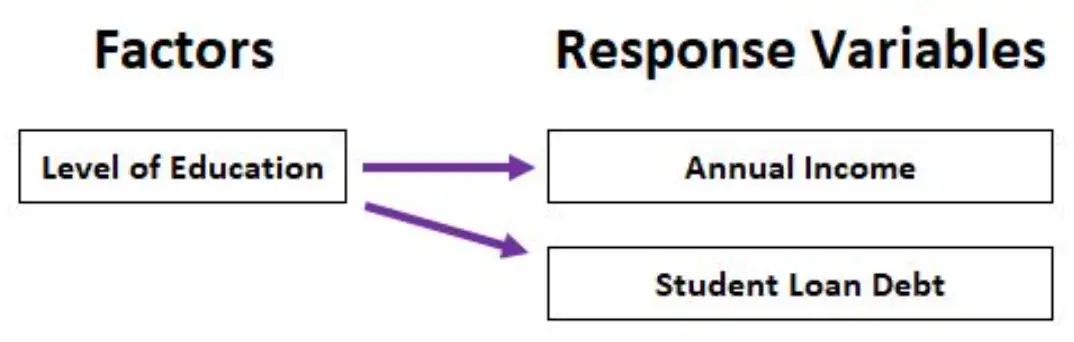
उदाहरण के लिए, हम यह विश्लेषण करने के लिए MANOVA का उपयोग कर सकते हैं कि शिक्षा स्तर (हाई स्कूल डिप्लोमा, एसोसिएट डिग्री, स्नातक डिग्री, मास्टर डिग्री) वार्षिक आय और कुल छात्र ऋण ऋण दोनों को कैसे प्रभावित करता है।

संबंधित: एनोवा, एन्कोवा, मानोवा और मनकोवा के बीच अंतर

हर बार जब हम MANOVA करते हैं, तो हमें यह सत्यापित करना होगा कि निम्नलिखित धारणाएँ पूरी हुई हैं:

1. बहुभिन्नरूपी सामान्यता – प्रतिक्रिया चर आमतौर पर कारक चर के प्रत्येक समूह के भीतर बहुभिन्नरूपी रूप से वितरित होते हैं।

2. स्वतंत्रता – प्रत्येक अवलोकन को जनसंख्या से यादृच्छिक रूप से और स्वतंत्र रूप से नमूना लिया जाता है।

3. समान प्रसरण – प्रत्येक समूह की जनसंख्या सहप्रसरण मैट्रिक्स समान हैं।

4. कोई बहुभिन्नरूपी आउटलेर नहीं – कोई अत्यधिक बहुभिन्नरूपी आउटलेर नहीं हैं।

इस लेख में, हम प्रत्येक धारणा का स्पष्टीकरण प्रदान करते हैं और साथ ही यह कैसे निर्धारित करें कि धारणा पूरी हुई है या नहीं।

धारणा 1: बहुभिन्नरूपी सामान्यता

एक MANOVA मानता है कि प्रतिक्रिया चर बहुभिन्नरूपी होते हैं जो आमतौर पर कारक चर के प्रत्येक समूह के भीतर वितरित होते हैं।

यदि प्रत्येक कारक * प्रतिक्रिया चर संयोजन के लिए कम से कम 20 अवलोकन हैं, तो हम मान सकते हैं कि बहुभिन्नरूपी सामान्यता की धारणा पूरी हो गई है।

यदि प्रत्येक कारक*प्रतिक्रिया चर संयोजन के लिए 20 से कम अवलोकन हैं, तो हम अवशेषों की कल्पना करने के लिए एक स्कैटरप्लॉट मैट्रिक्स बना सकते हैं और यह धारणा पूरी हुई है या नहीं, इसकी जांच कर सकते हैं।

सौभाग्य से, यह सर्वविदित है कि MANOVA बहुभिन्नरूपी सामान्यता से विचलन के प्रति मजबूत है, इसलिए छोटे से मध्यम विचलन आम तौर पर कोई समस्या नहीं हैं।

परिकल्पना 2: स्वतंत्रता

एक MANOVA मानता है कि प्रत्येक अवलोकन यादृच्छिक रूप से और स्वतंत्र रूप से जनसंख्या से नमूना लिया गया है।

जब तक डेटा एकत्र करने के लिए संभाव्यता नमूनाकरण विधि (जनसंख्या के प्रत्येक सदस्य के नमूने में चुने जाने की समान संभावना होती है) का उपयोग किया जाता है, हम मान सकते हैं कि प्रत्येक अवलोकन का नमूना यादृच्छिक और स्वतंत्र तरीके से किया गया था।

संभाव्यता नमूनाकरण विधियों के उदाहरणों में शामिल हैं:

• सामान्य उद्देश्यरहित नमूना
• स्तरीकृत यादृच्छिक नमूना
• यादृच्छिक क्लस्टर नमूनाकरण
• व्यवस्थित यादृच्छिक नमूनाकरण

धारणा 3: समान विचरण

एक MANOVA मानता है कि प्रत्येक समूह की जनसंख्या सहप्रसरण मैट्रिक्स समान हैं।

इस परिकल्पना का परीक्षण करने का सबसे आम तरीका बॉक्स के एम परीक्षण का उपयोग करना है। यह परीक्षण काफी सख्त माना जाता है, यही कारण है कि हम आम तौर पर यह निर्धारित करने के लिए 0.001 के महत्व स्तर का उपयोग करते हैं कि जनसंख्या सहप्रसरण मैट्रिक्स बराबर हैं या नहीं।

यदि बॉक्स के एम परीक्षण का पी-मान 0.001 से अधिक है, तो हम मान सकते हैं कि यह धारणा पूरी हो गई है।

सौभाग्य से, भले ही परीक्षण का पी-मान 0.001 से कम हो, एक MANOVA इस परिकल्पना से विचलन के लिए मजबूत होता है।

गैर-समान सहप्रसरण मैट्रिक्स के लिए एक समस्या होने के लिए, सहप्रसरण मैट्रिक्स के बीच अंतर काफी चरम होना चाहिए।

परिकल्पना 4: कोई बहुभिन्नरूपी आउटलेर नहीं

एक MANOVA मानता है कि डेटा में कोई अत्यधिक बहुभिन्नरूपी आउटलेर मौजूद नहीं हैं जो परिणामों को महत्वपूर्ण रूप से प्रभावित कर सकते हैं।

इस धारणा को सत्यापित करने का सबसे आम तरीका प्रत्येक अवलोकन के लिए महालनोबिस दूरी की गणना करना है, जो एक बहुभिन्नरूपी स्थान में दो बिंदुओं के बीच की दूरी का प्रतिनिधित्व करता है।

यदि किसी अवलोकन की महालनोबिस दूरी के लिए संबंधित पी-मान 0.001 से कम है, तो हम आम तौर पर उस अवलोकन को अत्यधिक बाहरी घोषित करते हैं।

विभिन्न सांख्यिकीय सॉफ़्टवेयर में महालनोबिस दूरी की गणना कैसे करें, यह देखने के लिए निम्नलिखित ट्यूटोरियल देखें:

• आर में महालनोबिस दूरी की गणना कैसे करें
• एसपीएसएस में महालनोबिस दूरी की गणना कैसे करें
• पायथन में महालनोबिस दूरी की गणना कैसे करें

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर में MANOVA कैसे निष्पादित करें:

R में MANOVA कैसे निष्पादित करें
SPSS में MANOVA कैसे निष्पादित करें
स्टाटा में MANOVA कैसे निष्पादित करें