स्टाटा में manova कैसे निष्पादित करें

एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि व्याख्यात्मक चर के विभिन्न स्तर कुछ प्रतिक्रिया चर में सांख्यिकीय रूप से भिन्न परिणाम देते हैं या नहीं।

उदाहरण के लिए, हमें यह समझने में रुचि हो सकती है कि क्या शिक्षा के तीन स्तरों (एसोसिएट की डिग्री, स्नातक की डिग्री, मास्टर डिग्री) से सांख्यिकीय रूप से अलग-अलग वार्षिक आय होती है या नहीं। इस मामले में हमारे पास एक व्याख्यात्मक चर और एक प्रतिक्रिया चर है।

• व्याख्यात्मक चर: शिक्षा का स्तर
• प्रतिक्रिया चर: वार्षिक आय

MANOVA एकतरफ़ा ANOVA का विस्तार है जिसमें एक से अधिक प्रतिक्रिया चर होते हैं। उदाहरण के लिए, हमें यह समझने में रुचि हो सकती है कि शिक्षा का स्तर अलग-अलग वार्षिक आय और छात्र ऋण की अलग-अलग मात्रा का कारण बनता है या नहीं। इस मामले में, हमारे पास एक व्याख्यात्मक चर और दो प्रतिक्रिया चर हैं:

• व्याख्यात्मक चर: शिक्षा का स्तर
• प्रतिक्रिया चर: वार्षिक आय, छात्र ऋण

चूँकि हमारे पास एक से अधिक प्रतिक्रिया चर हैं, इसलिए इस मामले में MANOVA का उपयोग करना उचित होगा।

आगे, हम बताएंगे कि स्टेटा में MANOVA कैसे निष्पादित करें।

उदाहरण: स्टाटा में मनोवा

यह समझाने के लिए कि स्टैटा में MANOVA कैसे निष्पादित किया जाए, हम निम्नलिखित डेटासेट का उपयोग करेंगे जिसमें 24 लोगों के लिए निम्नलिखित तीन चर शामिल हैं:

• शिक्षा: अध्ययन का स्तर (0 = एसोसिएट, 1 = बैचलर, 2 = मास्टर)
• आय: वार्षिक आय
• ऋण: कुल छात्र ऋण ऋण

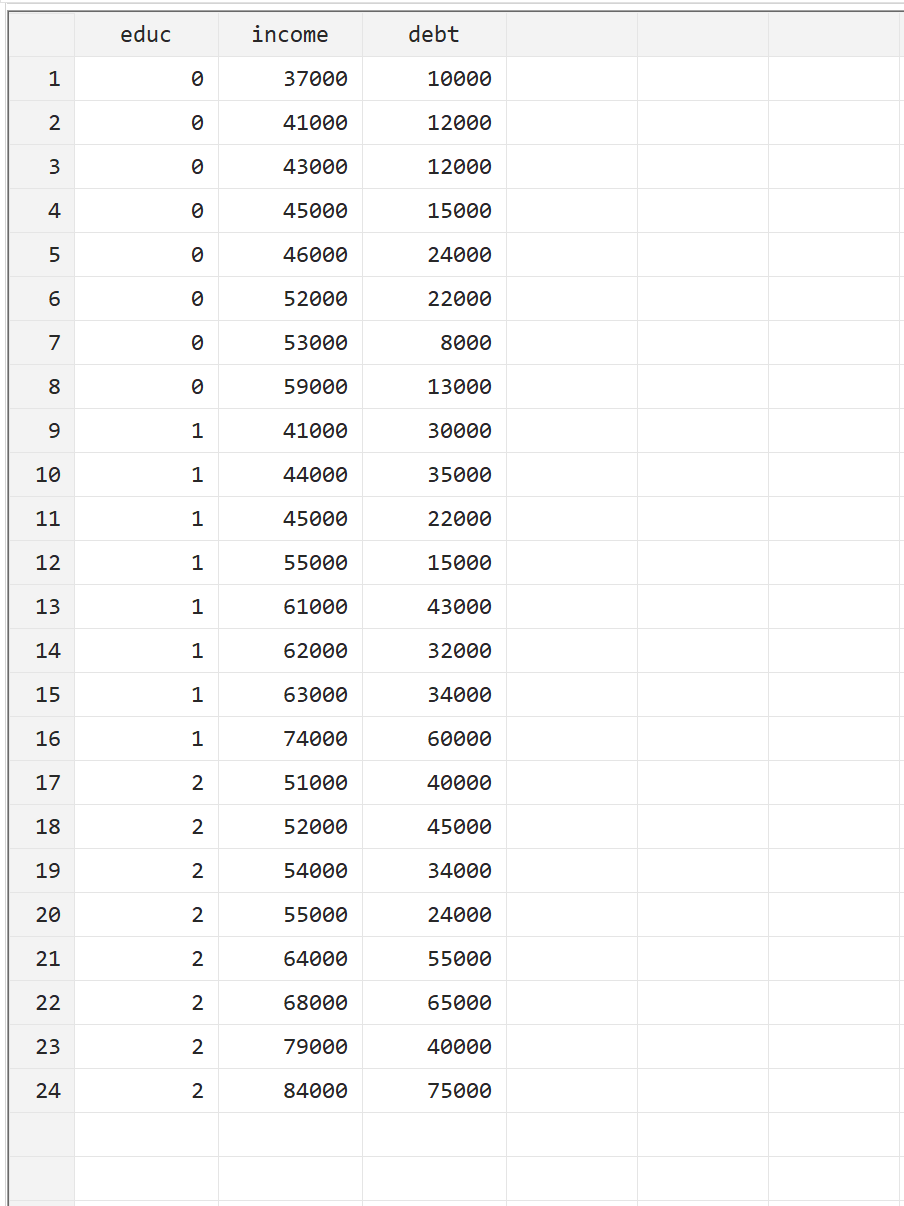
आप शीर्ष मेनू बार में डेटा > डेटा संपादक > डेटा संपादक (संपादन) पर नेविगेट करके मैन्युअल रूप से डेटा दर्ज करके इस उदाहरण को पुन: उत्पन्न कर सकते हैं।

व्याख्यात्मक चर के रूप में शिक्षा और प्रतिक्रिया चर के रूप में आय और ऋण का उपयोग करके MANOVA निष्पादित करने के लिए, हम निम्नलिखित कमांड का उपयोग कर सकते हैं:

आय ऋण मनोवा = शिक्षा

स्टाटा उनके संगत पी-मानों के साथ चार अद्वितीय परीक्षण आँकड़े तैयार करता है:

विल्क्स लैम्ब्डा: एफ आँकड़ा = 5.02, पी मान = 0.0023।

पिल्लई ट्रेस: एफ आँकड़ा = 4.07, पी मान = 0.0071।

लॉली-होटलिंग ट्रेस: एफ आँकड़ा = 5.94, पी मान = 0.0008।

सबसे बड़ा रॉय रूट: एफ-स्टेटिस्टिक = 13.10, पी-वैल्यू = 0.0002।

प्रत्येक परीक्षण आँकड़े की गणना कैसे की जाती है, इसकी विस्तृत व्याख्या के लिए, पेन स्टेट एबर्ली कॉलेज ऑफ़ साइंस का यह लेख देखें।

प्रत्येक परीक्षण आँकड़े के लिए पी-मान 0.05 से कम है, इसलिए शून्य परिकल्पना अस्वीकार कर दी जाएगी चाहे आप किसी भी परिकल्पना का उपयोग करें। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि शिक्षा का स्तर वार्षिक आय और कुल छात्र ऋण में सांख्यिकीय रूप से महत्वपूर्ण अंतर का कारण बनता है।

पी-वैल्यू पर ध्यान दें: आउटपुट तालिका में पी-वैल्यू के आगे का अक्षर बताता है कि एफ आंकड़े की गणना कैसे की गई (ई = सटीक गणना, ए = अनुमानित गणना, यू = ऊपरी सीमा)।