मशीन लर्निंग में ओवरफिटिंग क्या है? (स्पष्टीकरण एवं उदाहरण)

मशीन लर्निंग में, हम अक्सर मॉडल बनाते हैं ताकि हम कुछ घटनाओं के बारे में सटीक भविष्यवाणी कर सकें।

उदाहरण के लिए, मान लीजिए कि हम एक प्रतिगमन मॉडल बनाना चाहते हैं जो हाई स्कूल के छात्रों के लिए प्रतिक्रिया चर के एसीटी स्कोर की भविष्यवाणी करने के लिए अध्ययन में बिताए गए भविष्यवक्ता चर घंटों का उपयोग करता है।

इस मॉडल को बनाने के लिए, हम एक निश्चित स्कूल जिले में सैकड़ों छात्रों के लिए पढ़ाई में बिताए गए घंटों और संबंधित ACT स्कोर पर डेटा एकत्र करेंगे।

फिर हम इस डेटा का उपयोग एक मॉडल को प्रशिक्षित करने के लिए करेंगे जो अध्ययन किए गए घंटों की कुल संख्या के आधार पर किसी छात्र को प्राप्त होने वाले स्कोर के बारे में भविष्यवाणी कर सकता है।

मॉडल की उपयोगिता का आकलन करने के लिए, हम माप सकते हैं कि मॉडल की भविष्यवाणियाँ देखे गए डेटा से कितनी अच्छी तरह मेल खाती हैं। ऐसा करने के लिए सबसे अधिक उपयोग की जाने वाली मीट्रिक में से एक माध्य वर्ग त्रुटि (MSE) है, जिसकी गणना निम्नानुसार की जाती है:

एमएसई = (1/एन)*Σ(वाई _आई – एफ(एक्स _आई )) ²

सोना:

• n: अवलोकनों की कुल संख्या
• y _i : ^iवें अवलोकन का प्रतिक्रिया मूल्य
• f(x _i ): i ^वें अवलोकन का अनुमानित प्रतिक्रिया मूल्य

मॉडल की भविष्यवाणियां अवलोकनों के जितनी करीब होंगी, एमएसई उतना ही कम होगा।

हालाँकि, मशीन लर्निंग में की गई सबसे बड़ी गलतियों में से एक प्रशिक्षण एमएसई को कम करने के लिए मॉडल को अनुकूलित करना है, अर्थात, मॉडल की भविष्यवाणी उस डेटा से कितनी अच्छी तरह मेल खाती है जिसका उपयोग हमने मॉडल को प्रशिक्षित करने के लिए किया था।

जब कोई मॉडल प्रशिक्षण एमएसई को कम करने पर बहुत अधिक ध्यान केंद्रित करता है, तो उसे अक्सर प्रशिक्षण डेटा में ऐसे पैटर्न ढूंढने में बहुत मेहनत करनी पड़ती है जो केवल संयोग से होते हैं। फिर, जब मॉडल को अनदेखे डेटा पर लागू किया जाता है, तो इसका प्रदर्शन खराब होता है।

इस घटना को ओवरफिटिंग के रूप में जाना जाता है। ऐसा तब होता है जब हम किसी मॉडल को प्रशिक्षण डेटा के बहुत करीब से “फिट” करते हैं और इस प्रकार एक ऐसा मॉडल बनाते हैं जो नए डेटा पर भविष्यवाणियां करने के लिए उपयोगी नहीं होता है।

ओवरफिटिंग का उदाहरण

ओवरफिटिंग को समझने के लिए, आइए एक प्रतिगमन मॉडल बनाने के उदाहरण पर वापस लौटें जो ACT स्कोर की भविष्यवाणी करने के लिए अध्ययन में बिताए गए घंटों का उपयोग करता है।

मान लीजिए कि हम एक निश्चित स्कूल जिले में 100 छात्रों के लिए डेटा इकट्ठा करते हैं और दो चर के बीच संबंध की कल्पना करने के लिए एक त्वरित स्कैटरप्लॉट बनाते हैं:

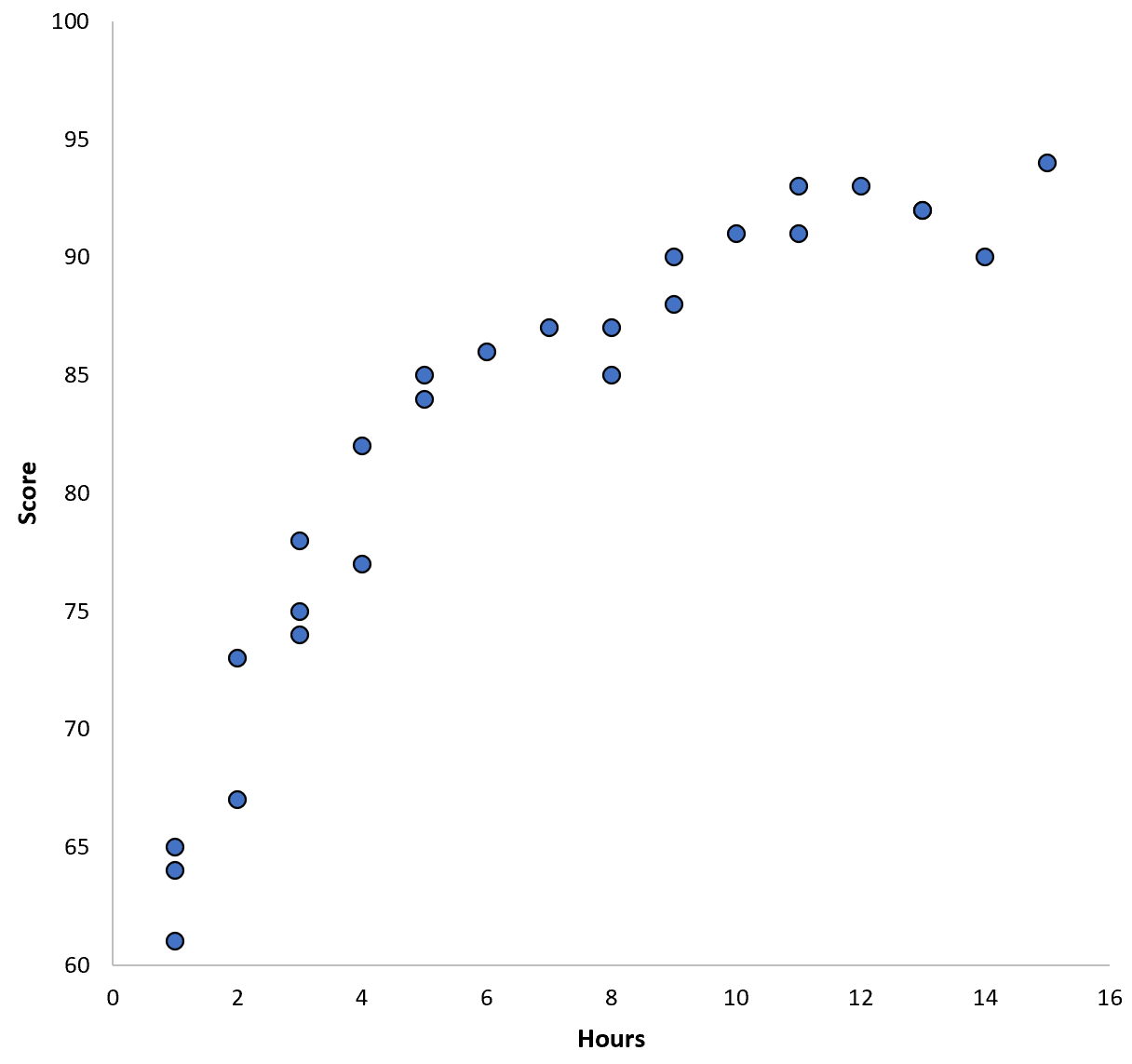
दो चरों के बीच का संबंध द्विघात प्रतीत होता है, इसलिए मान लीजिए कि हम निम्नलिखित द्विघात प्रतिगमन मॉडल लागू करते हैं:

स्कोर = 60.1 + 5.4*(घंटे) – 0.2*(घंटे) ²

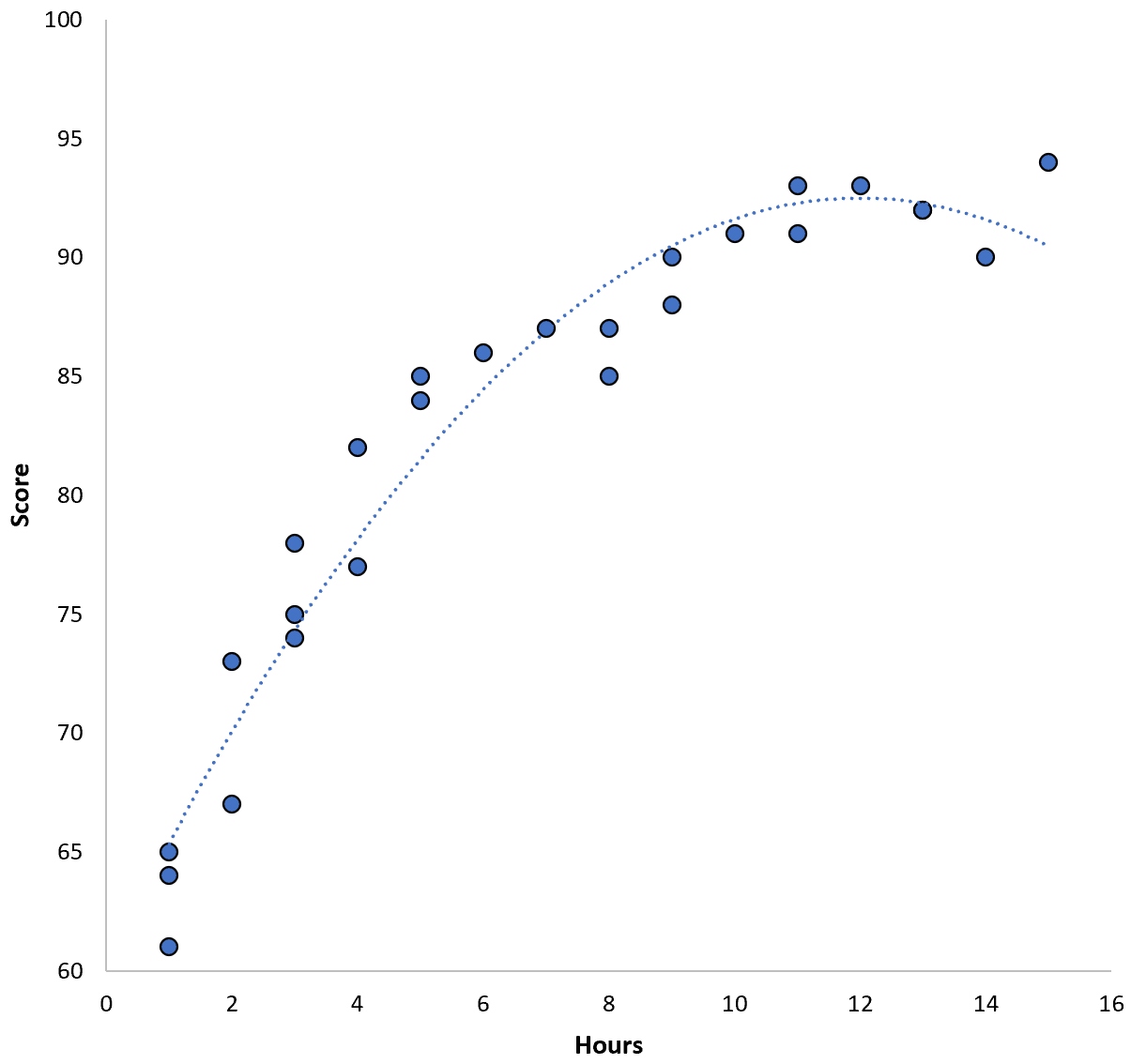
इस मॉडल में 3.45 की प्रशिक्षण माध्य वर्ग त्रुटि (MSE) है। अर्थात्, मॉडल द्वारा की गई भविष्यवाणियों और वास्तविक ACT स्कोर के बीच मूल माध्य वर्ग अंतर 3.45 है।

हालाँकि, हम उच्च क्रम के बहुपद मॉडल को फिट करके इस प्रशिक्षण एमएसई को कम कर सकते हैं। उदाहरण के लिए, मान लीजिए कि हम निम्नलिखित मॉडल लागू करते हैं:

स्कोर = 64.3 – 7.1*(घंटे) + 8.1*(घंटे) ² – 2.1*(घंटे) ³ + 0.2*(घंटे ^{) 4 – 0.1*(घंटे) 5 +} 0.2(घंटे) ⁶

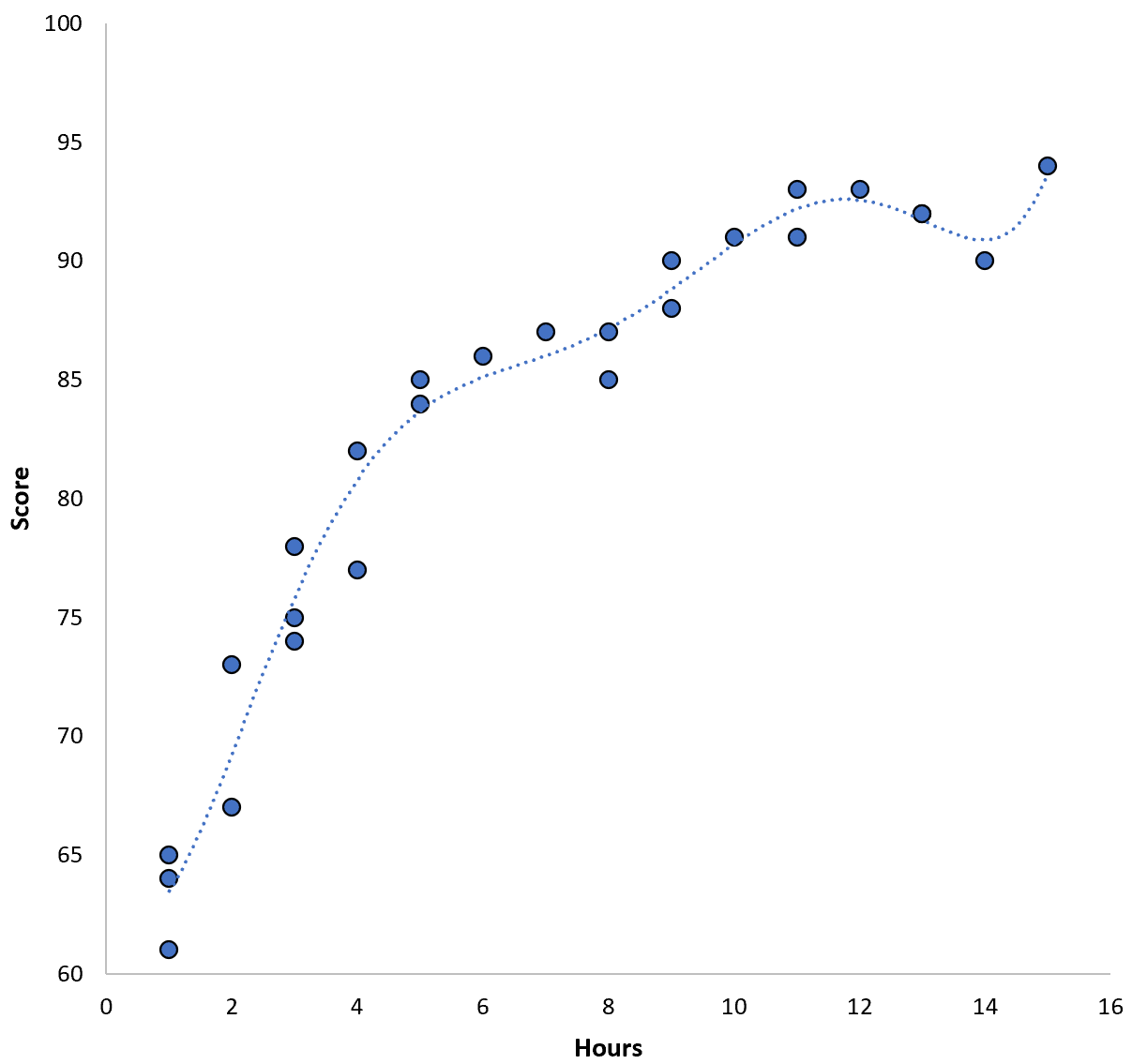
ध्यान दें कि कैसे प्रतिगमन रेखा पिछली प्रतिगमन रेखा की तुलना में वास्तविक डेटा को अधिक बारीकी से फिट करती है।

इस मॉडल में प्रशिक्षण मूल माध्य वर्ग त्रुटि (MSE) केवल 0.89 है। अर्थात्, मॉडल द्वारा की गई भविष्यवाणियों और वास्तविक ACT स्कोर के बीच मूल माध्य वर्ग अंतर 0.89 है।

यह एमएसई प्रशिक्षण पिछले मॉडल द्वारा उत्पादित प्रशिक्षण की तुलना में बहुत छोटा है।

हालाँकि, हम वास्तव में प्रशिक्षण एमएसई के बारे में परवाह नहीं करते हैं, अर्थात, मॉडल की भविष्यवाणियाँ उस डेटा से कितनी अच्छी तरह मेल खाती हैं जिसका उपयोग हमने मॉडल को प्रशिक्षित करने के लिए किया था। इसके बजाय, हम मुख्य रूप से एमएसई परीक्षण – एमएसई की परवाह करते हैं जब हमारा मॉडल अनदेखे डेटा पर लागू होता है।

यदि हमने उपरोक्त उच्च क्रम बहुपद प्रतिगमन मॉडल को एक अदृश्य डेटासेट पर लागू किया है, तो यह संभवतः सरल द्विघात प्रतिगमन मॉडल से भी बदतर प्रदर्शन करेगा। यानी, यह उच्चतर एमएसई परीक्षण उत्पन्न करेगा, जो कि वास्तव में हम नहीं चाहते हैं।

ओवरफिटिंग का पता कैसे लगाएं और उससे कैसे बचें

ओवरफिटिंग का पता लगाने का सबसे आसान तरीका क्रॉस-वैलिडेशन करना है। सबसे अधिक इस्तेमाल की जाने वाली विधि को के-फोल्ड क्रॉस-वैलिडेशन के रूप में जाना जाता है और यह निम्नानुसार काम करती है:

चरण 1: किसी डेटा सेट को यादृच्छिक रूप से लगभग समान आकार के k समूहों, या “फ़ोल्ड्स” में विभाजित करें।

चरण 2: अपने होल्डिंग सेट के रूप में किसी एक तह को चुनें। टेम्पलेट को शेष k-1 फ़ोल्ड में समायोजित करें। तनावग्रस्त प्लाई में अवलोकनों पर एमएसई परीक्षण की गणना करें।

चरण 3: इस प्रक्रिया को k बार दोहराएं, हर बार बहिष्करण सेट के रूप में एक अलग सेट का उपयोग करें।

चरण 4: परीक्षण के k MSE के औसत के रूप में परीक्षण के समग्र MSE की गणना करें।

परीक्षण एमएसई = (1/के)*Σएमएसई _i

सोना:

• k: तहों की संख्या
• एमएसई _i : ^{आईटीएच} पुनरावृत्ति पर एमएसई का परीक्षण करें

यह एमएसई परीक्षण हमें एक अच्छा विचार देता है कि कोई दिया गया मॉडल अज्ञात डेटा पर कैसा प्रदर्शन करेगा।

व्यवहार में, हम कई अलग-अलग मॉडलों को फिट कर सकते हैं और इसके एमएसई परीक्षण का पता लगाने के लिए प्रत्येक मॉडल पर के-फोल्ड क्रॉस-सत्यापन कर सकते हैं। फिर हम भविष्य में पूर्वानुमान लगाने के लिए सबसे अच्छे मॉडल के रूप में सबसे कम एमएसई परीक्षण वाले मॉडल को चुन सकते हैं।

यह सुनिश्चित करता है कि हम एक ऐसे मॉडल का चयन करते हैं जो भविष्य के डेटा पर सबसे अच्छा प्रदर्शन करने की संभावना रखता है, उस मॉडल के विपरीत जो केवल प्रशिक्षण एमएसई को कम करता है और ऐतिहासिक डेटा के लिए अच्छी तरह से “फिट” होता है।

अतिरिक्त संसाधन

मशीन लर्निंग में पूर्वाग्रह-विचरण ट्रेडऑफ़ क्या है?
के-फोल्ड क्रॉस-वैलिडेशन का एक परिचय
मशीन लर्निंग में प्रतिगमन और वर्गीकरण मॉडल