माध्य, माध्यिका और बहुलक

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि माध्य, माध्यिका और बहुलक क्या हैं। आप सीखेंगे कि माध्य, माध्यिका और बहुलक कैसे प्राप्त करें, उनका उपयोग किस लिए किया जाता है और इन तीन सांख्यिकीय उपायों के बीच क्या अंतर है। इसके अतिरिक्त, आप अंत में ऑनलाइन कैलकुलेटर के साथ किसी भी सांख्यिकीय नमूने के माध्य, माध्यिका और मोड की गणना करने में सक्षम होंगे।

माध्य, माध्यिका और बहुलक क्या है?

माध्य, माध्यिका और बहुलक केंद्रीय स्थिति के सांख्यिकीय माप हैं। दूसरे शब्दों में, माध्य, माध्य और मोड वे मान हैं जो एक सांख्यिकीय नमूने को परिभाषित करने में मदद करते हैं, विशेष रूप से, वे इंगित करते हैं कि इसके केंद्रीय मूल्य क्या हैं।

माध्य, माध्यिका और बहुलक को इस प्रकार परिभाषित किया गया है:

माध्य : नमूने में सभी डेटा का औसत है।
माध्यिका : यह सबसे छोटे से सबसे बड़े तक क्रमित सभी डेटा का मध्य मान है।
मोड : यह डेटासेट में सबसे अधिक दोहराया जाने वाला मान है।

इन तीन सांख्यिकीय उपायों को नीचे अधिक विस्तार से समझाया गया है।

आधा

औसत की गणना करने के लिए, सभी मान जोड़ें और फिर डेटा की कुल संख्या से विभाजित करें। इसलिए औसत का सूत्र इस प्रकार है:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

👉 आप किसी भी डेटा सेट के माध्य, माध्यिका और मोड की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

औसत प्रतीक अक्षर x के ऊपर एक क्षैतिज बैंड है

$(\overline{x}).$

आप माध्य प्रतीक के साथ नमूना माध्य को जनसंख्या माध्य से अलग भी कर सकते हैं: एक नमूने का माध्य प्रतीक के साथ व्यक्त किया जाता है

$\overline{x}$

, जबकि जनसंख्या का औसत ग्रीक अक्षर का उपयोग करता है

$\mu.$

औसत को अंकगणितीय माध्य या औसत के रूप में भी जाना जाता है। इसके अलावा, एक सांख्यिकीय वितरण का माध्य इसकी गणितीय अपेक्षा के बराबर है।

औसत उदाहरण

एक छात्र ने स्कूल वर्ष के दौरान निम्नलिखित ग्रेड हासिल किए: गणित में 9, भाषा में 7, इतिहास में 6, अर्थशास्त्र में 8 और विज्ञान में 7.5। आपके सभी ग्रेडों का औसत क्या है?

अंकगणितीय औसत ज्ञात करने के लिए, हमें सभी ग्रेडों को जोड़ना होगा और फिर पाठ्यक्रम में विषयों की कुल संख्या से विभाजित करना होगा, जो कि 5 है। इसलिए, हम अंकगणितीय औसत सूत्र लागू करते हैं:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

हम डेटा को सूत्र में प्रतिस्थापित करते हैं और अंकगणितीय माध्य की गणना करते हैं:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

जैसा कि आप देख सकते हैं, अंकगणितीय औसत में, प्रत्येक मान को समान भार दिया जाता है, अर्थात, डेटा के प्रत्येक टुकड़े का संपूर्ण भार समान होता है।

मंझला

माध्यिका सबसे छोटे से लेकर सबसे बड़े तक क्रमित सभी डेटा का मध्य मान है। दूसरे शब्दों में, माध्य क्रमित डेटा सेट को दो बराबर भागों में विभाजित करता है।

माध्यिका की गणना इस बात पर निर्भर करती है कि डेटा की कुल संख्या सम है या विषम:

यदि डेटा की कुल संख्या विषम है, तो माध्यिका वह मान होगा जो डेटा के ठीक बीच में आता है। कहने का तात्पर्य यह है कि वह मान जो क्रमबद्ध डेटा की स्थिति (n+1)/2 में है।

$Me=x_{\frac{n+1}{2}$

यदि डेटा बिंदुओं की कुल संख्या सम है, तो माध्य केंद्र में स्थित दो डेटा बिंदुओं का औसत होगा। यानी उन मानों का अंकगणितीय औसत जो ऑर्डर किए गए डेटा के स्थानों n/2 और n/2+1 पर पाए जाते हैं।

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

सोना

$n$

नमूने में डेटा आइटम की कुल संख्या है।

मी शब्द का प्रयोग अक्सर यह दर्शाने के लिए एक प्रतीक के रूप में किया जाता है कि एक मान सभी अवलोकनों का माध्यिका है।

माध्यिका उदाहरण

निम्नलिखित डेटा का माध्य ज्ञात कीजिए: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

गणना करने से पहले सबसे पहली चीज़ डेटा को वर्गीकृत करना है, यानी हम संख्याओं को सबसे छोटे से सबसे बड़े तक रखते हैं।

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

इस मामले में हमारे पास 11 अवलोकन हैं, इसलिए डेटा की कुल संख्या विषम है। इसलिए, हम माध्यिका की स्थिति की गणना करने के लिए निम्नलिखित सूत्र लागू करते हैं:

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

इसलिए माध्यिका छठे स्थान पर स्थित डेटा होगा, जो इस मामले में मान 4 से मेल खाता है।

$Me=x_6=4$

पहनावा

आँकड़ों में, मोड डेटा सेट में वह मान है जिसकी निरपेक्ष आवृत्ति सबसे अधिक है, अर्थात, मोड डेटा सेट में सबसे अधिक दोहराया जाने वाला मान है।

इसलिए, सांख्यिकीय डेटा सेट के मोड की गणना करने के लिए, बस नमूने में प्रत्येक डेटा तत्व के प्रकट होने की संख्या की गणना करें, और सबसे अधिक दोहराया जाने वाला डेटा मोड होगा।

मोड को सांख्यिकीय मोड या मोडल वैल्यू भी कहा जा सकता है। इसी प्रकार, जब डेटा को अंतरालों में समूहीकृत किया जाता है, तो सबसे अधिक दोहराया जाने वाला अंतराल मोडल अंतराल या मोडल वर्ग होता है।

सामान्य तौर पर, मो शब्द का उपयोग सांख्यिकीय मोड के प्रतीक के रूप में किया जाता है, उदाहरण के लिए, वितरण मोड एक्स मो (एक्स) है।

सर्वाधिक दोहराए गए मानों की संख्या के अनुसार तीन प्रकार के मोड को प्रतिष्ठित किया जा सकता है:

यूनिमॉडल मोड : अधिकतम संख्या में दोहराव के साथ केवल एक मान होता है। उदाहरण के लिए, [1, 4, 2, 4, 5, 3]।
बिमोडल मोड : दोहराव की अधिकतम संख्या दो अलग-अलग मानों पर होती है, और दोनों मान समान संख्या में दोहराए जाते हैं। उदाहरण के लिए, [2, 6, 7, 2, 3, 6, 9]।
मल्टीमॉडल मोड : तीन या अधिक मानों में दोहराव की अधिकतम संख्या समान होती है। उदाहरण के लिए, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1]।

फैशन उदाहरण

निम्नलिखित डेटासेट का मोड क्या है?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

संख्याएँ क्रम से बाहर हैं, इसलिए पहली चीज़ जो हम करेंगे वह उन्हें क्रमबद्ध करना है। यह कदम अनिवार्य नहीं है, लेकिन यह आपको अधिक आसानी से फैशन ढूंढने में मदद करेगा।

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

संख्या 2 और 9 दो बार आती हैं, लेकिन संख्या 5 तीन बार दोहराई जाती है। इसलिए, डेटा श्रृंखला का मोड संख्या 5 है।

$Mo=5$

माध्य, माध्यिका और बहुलक का हल किया गया अभ्यास

अब जब आप जानते हैं कि माध्य, माध्य और बहुलक क्या हैं, तो नीचे इन सांख्यिकीय उपायों पर एक विस्तृत अभ्यास दिया गया है ताकि आप देख सकें कि उनकी गणना कैसे की जाती है।

निम्नलिखित सांख्यिकीय डेटा सेट का माध्य, माध्यिका और मोड ज्ञात करें:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

डेटा का औसत ज्ञात करने के लिए, हमें सभी को जोड़ना होगा, फिर डेटा की कुल संख्या से विभाजित करना होगा, जो कि 30 है:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}=\frac{192}{30}=6,4$

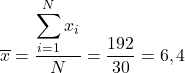
दूसरा, आइए नमूना माध्यिका ज्ञात करें। इसलिए हम सभी संख्याओं को आरोही क्रम में रखते हैं:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

इस मामले में, डेटा की कुल संख्या सम है, इसलिए उन दो केंद्रीय स्थितियों की गणना करना आवश्यक है जिनके बीच माध्यिका पाई जाएगी। इसके लिए हम निम्नलिखित दो सूत्रों का उपयोग करते हैं:

$\cfrac{n}{2}=\cfrac{30}{2}=15$

$\cfrac{n}{2}+1=\cfrac{30}{2}+1=16$

इसलिए माध्यिका पंद्रहवीं और सोलहवीं स्थिति के बीच होगी, जो क्रमशः 6 और 7 मानों से मेल खाती है। अधिक सटीक रूप से, माध्य इन मानों के औसत के बराबर है:

$Me=\cfrac{x_{15}+x_{16}}{2}=\cfrac{6+7}{2}=6,5$

अंत में, मोड ढूंढने के लिए आपको बस प्रत्येक संख्या के प्रकट होने पर सभी समय की गणना करनी होगी। जैसा कि आप देख सकते हैं, संख्या 6 और संख्या 8 कुल मिलाकर चार बार आती हैं, जो दोहराव की अधिकतम संख्या है। इसलिए, इस मामले में यह एक द्विमोडल मोड है और दो संख्याएँ डेटासेट का मोड हैं:

$Mo=\{ 6 \ ; \ 8\}$

माध्य, माध्यिका और मोड कैलकुलेटर

किसी भी सांख्यिकीय नमूने से उसके माध्य, माध्यिका और मोड की गणना करने के लिए निम्नलिखित ऑनलाइन कैलकुलेटर में डेटा दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने