माध्य और मानक विचलन के बीच संबंध (उदाहरण के साथ)

माध्य डेटा के एक सेट में औसत मान का प्रतिनिधित्व करता है।

इसकी गणना इस प्रकार की जाती है:

नमूना माध्य = Σx _i / n

सोना:

• Σ: एक प्रतीक जिसका अर्थ है “योग”
• x _i : डेटा सेट में i ^वां अवलोकन
• n: डेटासेट में अवलोकनों की कुल संख्या

मानक विचलन माध्य के सापेक्ष डेटा सेट में मूल्यों के वितरण का प्रतिनिधित्व करता है।

इसकी गणना इस प्रकार की जाती है:

नमूना मानक विचलन = √ Σ(x _i – x _bar ) ² / (n-1)

सोना:

• Σ: एक प्रतीक जिसका अर्थ है “योग”
• x _i : नमूने का ⁱ वां मान
• x _बार : नमूना का मतलब है
• n: नमूना आकार

माध्य और मानक विचलन के बीच संबंध पर ध्यान दें: माध्य का उपयोग मानक विचलन की गणना के लिए सूत्र में किया जाता है ।

वास्तव में, हम किसी नमूने के मानक विचलन की गणना तब तक नहीं कर सकते जब तक हमें नमूना माध्य न पता हो।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में डेटा सेट के लिए नमूना माध्य और नमूना मानक विचलन की गणना कैसे करें।

उदाहरण: डेटा सेट के लिए माध्य और मानक विचलन की गणना करना

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट है जो 10 अलग-अलग बास्केटबॉल खिलाड़ियों द्वारा बनाए गए अंक दिखाता है:

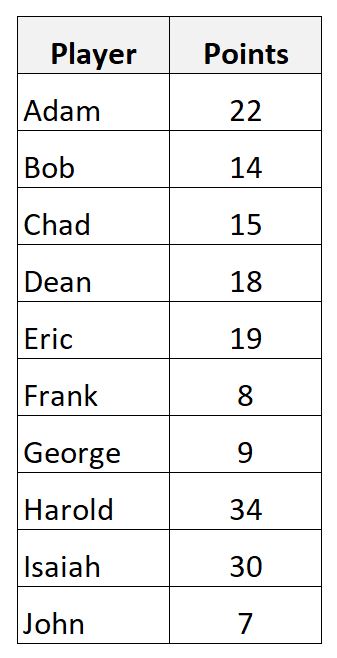हम निम्नलिखित सूत्र का उपयोग करके प्राप्त अंकों के नमूना औसत की गणना कर सकते हैं:

• नमूना माध्य = Σx _i / n
• नमूना औसत = (22+14+15+18+19+8+9+34+30+7) / 10
• नमूना माध्य = 17.6

अर्जित अंकों का नमूना औसत 17.6 है। यह सभी खिलाड़ियों के बीच प्राप्त अंकों की औसत संख्या को दर्शाता है।

एक बार जब हम नमूना माध्य जान लेते हैं, तो हम नमूना मानक विचलन की गणना करने के लिए इसे सूत्र में प्लग कर सकते हैं:

• नमूना मानक विचलन = √ Σ(x _i – x _bar ) ² / (n-1)
• नमूना मानक विचलन = √ ((22-17.6) ² + (14-17.6) ² + (15-17.6) ² + (18-17.6) ² + (19-17.6) 6) ² + (8-17.6) ² + (9 -17.6) ² + (34-17.6) ² + (30-17.6) ² + (7-17.6) ² ) / (10-1)
• नमूना मानक विचलन = 9.08

नमूना मानक विचलन 9.08 है। यह प्रत्येक बिंदु मान और नमूना बिंदु औसत के बीच की औसत दूरी को दर्शाता है।

किसी डेटा सेट का माध्य और मानक विचलन दोनों जानना उपयोगी है क्योंकि प्रत्येक मीट्रिक हमें कुछ अलग बताता है।

औसत हमें यह अंदाज़ा देता है कि डेटा सेट का “केंद्रीय” मान कहाँ स्थित है।

मानक विचलन हमें डेटा सेट में माध्य के आसपास मूल्यों के वितरण का एक विचार देता है। मानक विचलन मान जितना अधिक होगा, नमूने में मान उतने ही अधिक बिखरे हुए होंगे।

इन दो मूल्यों को जानकर, हम डेटा सेट में मूल्यों के वितरण के बारे में बहुत कुछ सीख सकते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल माध्य और मानक विचलन के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सांख्यिकी में औसत क्यों महत्वपूर्ण है?
सांख्यिकी में मानक विचलन क्यों महत्वपूर्ण है?
एक्सेल में माध्य और मानक विचलन की गणना कैसे करें