उत्पत्ति के माध्यम से प्रतिगमन: परिभाषा और उदाहरण

सरल रेखीय प्रतिगमन एक ऐसी विधि है जिसका उपयोग एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए किया जा सकता है।

एक सरल रैखिक प्रतिगमन मॉडल निम्नलिखित रूप लेता है:

y = β ₀ + β ₁ x

सोना:

• y : प्रतिक्रिया चर का मान
• β ₀ : प्रतिक्रिया चर का मान जब x = 0 (जिसे “अवरोधन” शब्द कहा जाता है)
• β ₁ : x में एक-इकाई वृद्धि के साथ जुड़े प्रतिक्रिया चर में औसत वृद्धि
• x : पूर्वानुमानित चर का मान

इस मॉडल के एक संशोधित संस्करण को मूल के माध्यम से प्रतिगमन के रूप में जाना जाता है, जो y को 0 के बराबर होने के लिए मजबूर करता है जब x 0 के बराबर होता है।

इस प्रकार का मॉडल निम्नलिखित रूप लेता है:

y = _β1x

ध्यान दें कि इंटरसेप्ट शब्द को मॉडल से पूरी तरह हटा दिया गया है।

इस मॉडल का उपयोग कभी-कभी तब किया जाता है जब शोधकर्ता जानते हैं कि जब भविष्यवक्ता चर शून्य होता है तो प्रतिक्रिया चर शून्य होना चाहिए।

वास्तविक दुनिया में, इस प्रकार के मॉडल का उपयोग अक्सर वानिकी या पारिस्थितिक अध्ययन में किया जाता है।

उदाहरण के लिए, शोधकर्ता पेड़ की ऊंचाई का अनुमान लगाने के लिए पेड़ की परिधि का उपयोग कर सकते हैं। यदि किसी पेड़ की परिधि शून्य है, तो उसकी ऊंचाई भी शून्य होनी चाहिए।

इसलिए, इस डेटा में एक प्रतिगमन मॉडल को फिट करते समय, मूल शब्द के गैर-शून्य होने का कोई मतलब नहीं होगा।

निम्नलिखित उदाहरण एक साधारण सरल रैखिक प्रतिगमन मॉडल को फिट करने और एक मॉडल जो मूल के माध्यम से प्रतिगमन को लागू करता है, के बीच अंतर दिखाता है।

उदाहरण: मूल के माध्यम से प्रतिगमन

मान लीजिए कि एक जीवविज्ञानी पेड़ की ऊंचाई का अनुमान लगाने के लिए पेड़ की परिधि का उपयोग करके एक प्रतिगमन मॉडल फिट करना चाहता है। वह बाहर जाती है और 15 पेड़ों के नमूने के लिए निम्नलिखित माप एकत्र करती है:

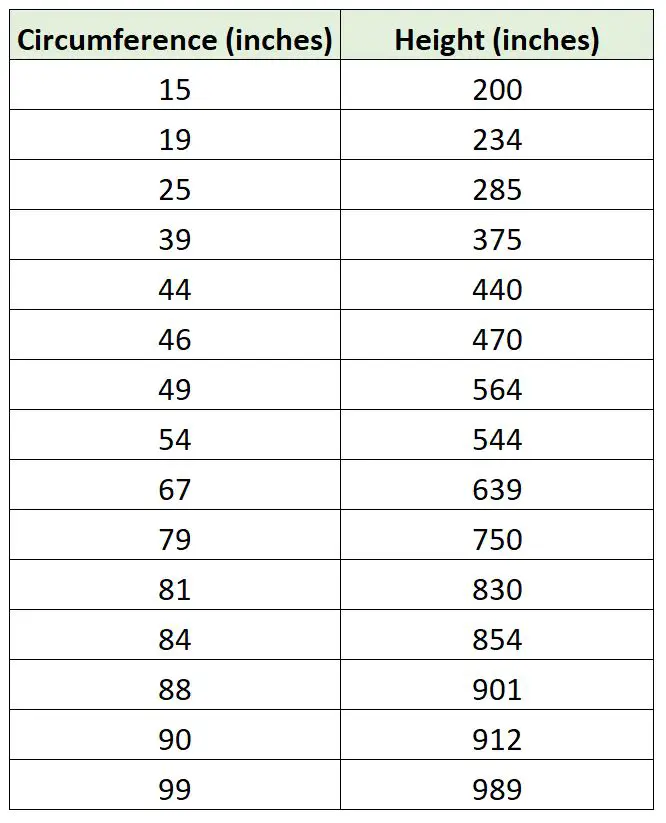
हम एक साधारण रैखिक प्रतिगमन मॉडल को एक प्रतिगमन मॉडल के साथ फिट करने के लिए आर में निम्नलिखित कोड का उपयोग कर सकते हैं जो बिना किसी अवरोध का उपयोग करता है और दो प्रतिगमन रेखाओं को प्लॉट करता है:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

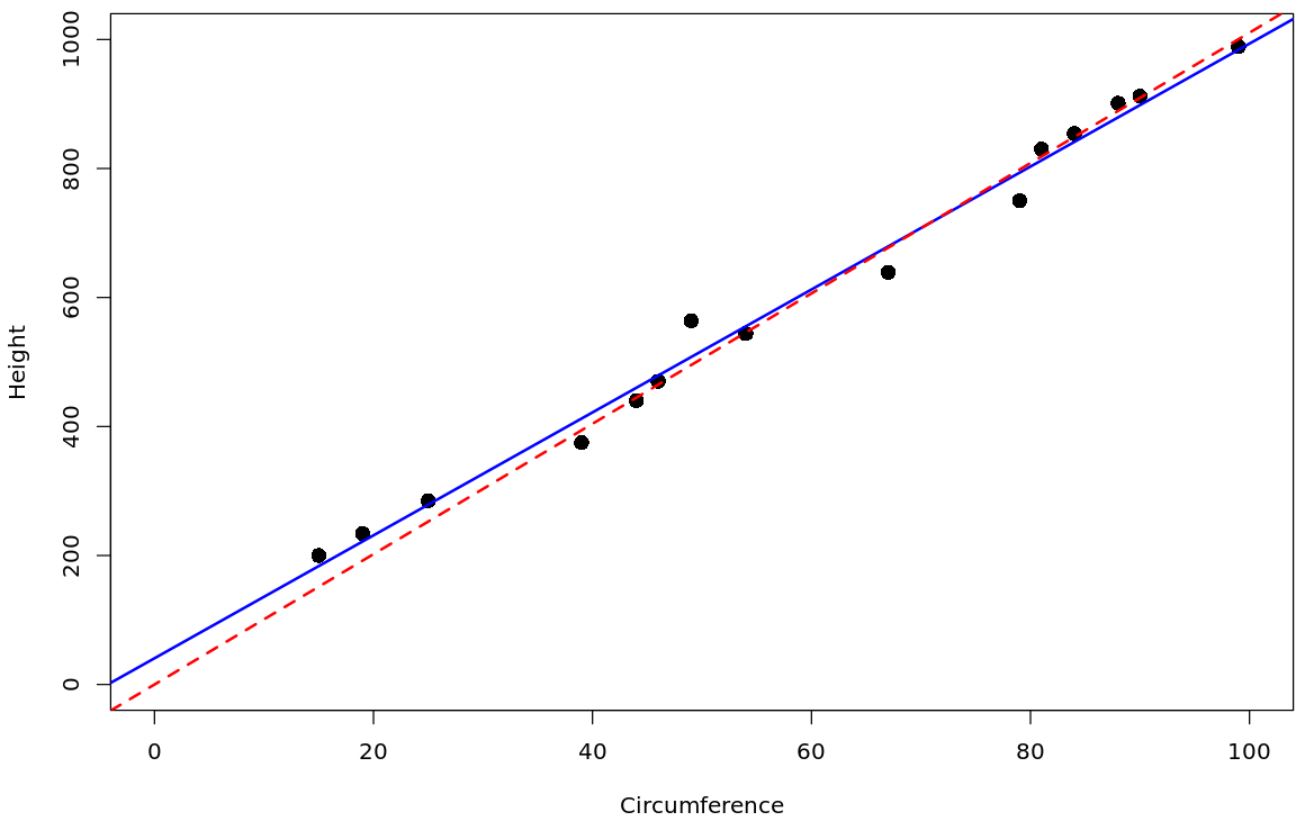
लाल बिंदीदार रेखा उस प्रतिगमन मॉडल का प्रतिनिधित्व करती है जो मूल से होकर गुजरती है, और नीली ठोस रेखा सामान्य सरल रैखिक प्रतिगमन मॉडल का प्रतिनिधित्व करती है।

हम प्रत्येक मॉडल के लिए गुणांक अनुमान प्राप्त करने के लिए आर में निम्नलिखित कोड का उपयोग कर सकते हैं:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

सरल रेखीय प्रतिगमन मॉडल के लिए फिट समीकरण है:

ऊँचाई = 40.6969 + 9.5296 (परिधि)

और मूल के माध्यम से प्रतिगमन मॉडल के लिए फिट समीकरण है:

ऊँचाई = 10.1057 (परिधि)

ध्यान दें कि परिधि चर के लिए गुणांक अनुमान थोड़ा अलग हैं।

उत्पत्ति के माध्यम से प्रतिगमन का उपयोग करने के लिए सावधानियां

इंटरसेप्ट रिग्रेशन का उपयोग करने से पहले, आपको पूरी तरह से आश्वस्त होना चाहिए कि भविष्यवक्ता चर के लिए 0 का मान प्रतिक्रिया चर के लिए 0 के मान को दर्शाता है। कई परिदृश्यों में, निश्चित रूप से जानना लगभग असंभव है।

और यदि आप उत्पत्ति का अनुमान लगाने में स्वतंत्रता की एक डिग्री बचाने के लिए मूल के माध्यम से प्रतिगमन का उपयोग करते हैं, तो यह शायद ही कभी महत्वपूर्ण अंतर लाता है यदि आपका नमूना आकार काफी बड़ा है।

यदि आप मूल के माध्यम से प्रतिगमन का उपयोग करना चुनते हैं, तो अपने अंतिम विश्लेषण या रिपोर्ट में अपने तर्क को रेखांकित करना सुनिश्चित करें।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल रैखिक प्रतिगमन के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सरल रेखीय प्रतिगमन का परिचय
एकाधिक रेखीय प्रतिगमन का परिचय
प्रतिगमन तालिका को कैसे पढ़ें और व्याख्या करें