मोरन का स्व क्या है? (परिभाषा & #038; उदाहरण)

मोरन का I स्थानिक स्वसहसंबंध को मापने का एक तरीका है।

सीधे शब्दों में कहें तो, यह यह मापने का एक तरीका है कि 2डी स्पेस में मूल्यों को कितनी बारीकी से क्लस्टर किया गया है। इसका उपयोग अक्सर भूगोल और भौगोलिक सूचना विज्ञान (जीआईएस) में यह मापने के लिए किया जाता है कि मानचित्र पर विभिन्न विशेषताओं को कितनी बारीकी से समूहीकृत किया गया है, जैसे कि घरेलू आय, शिक्षा स्तर, आदि।

मोरन का I: सूत्र

मोरान I की गणना करने का सूत्र है:

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

सोना:

• एन: आई और जे द्वारा अनुक्रमित स्थानिक इकाइयों की संख्या
• डब्ल्यू: सभी डब्ल्यू _आईजे का योग
• x: ब्याज का चर (घरेलू आय, स्कूली शिक्षा के वर्ष, आदि)
• x : x का औसत
• w _ij : स्थानिक भार का एक मैट्रिक्स

आपको शायद इस माप की गणना हाथ से कभी नहीं करनी पड़ेगी क्योंकि अधिकांश सांख्यिकीय सॉफ़्टवेयर आपके लिए इसकी गणना कर सकते हैं, लेकिन यह हुड के तहत उपयोग किए गए सूत्र को जानने में मदद करता है।

मोरन के I का मान -1 से 1 तक हो सकता है जहां:

• -1: रुचि का चर पूरी तरह से फैला हुआ है
• 0: रुचि का चर यादृच्छिक रूप से फैला हुआ है
• 1: रुचि का चर पूरी तरह से समूहीकृत है

मोरन के I की गणना के साथ-साथ, अधिकांश सांख्यिकीय सॉफ़्टवेयर संबंधित पी-वैल्यू की गणना करते हैं जिसका उपयोग यह निर्धारित करने के लिए किया जा सकता है कि डेटा यादृच्छिक रूप से फैला हुआ है या नहीं।

मोरन परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

शून्य परिकल्पना (H ₀ ): डेटा बेतरतीब ढंग से फैला हुआ है।

वैकल्पिक परिकल्पना ( _एचए ): डेटा को यादृच्छिक रूप से फैलाया नहीं जाता है, यानी, इसे दृश्यमान पैटर्न में समूहीकृत किया जाता है।

यदि पी-मान जो मोरन के I से मेल खाता है, एक निश्चित स्तर के महत्व से नीचे है (यानी α = 0.05), तो हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि डेटा स्थानिक रूप से क्लस्टर किया गया है, इसलिए उनके स्थानिक रूप से क्लस्टर होने की संभावना नहीं है। संयोग से हुआ.

मोरन का I: कुछ उदाहरण

निम्नलिखित उदाहरण मोरन के I के लिए विभिन्न मूल्यों वाले झूठे कार्ड दर्शाते हैं।

आइए मान लें कि मानचित्र पर प्रत्येक वर्ग एक काउंटी का प्रतिनिधित्व करता है, और $50,000 से अधिक औसत घरेलू आय वाले काउंटी को नीले रंग में दिखाया गया है।

मोरन का I = 0: औसत घरेलू आय बेतरतीब ढंग से बिखरी हुई है (यानी यादृच्छिक क्षेत्रों में यादृच्छिक क्लस्टर)।

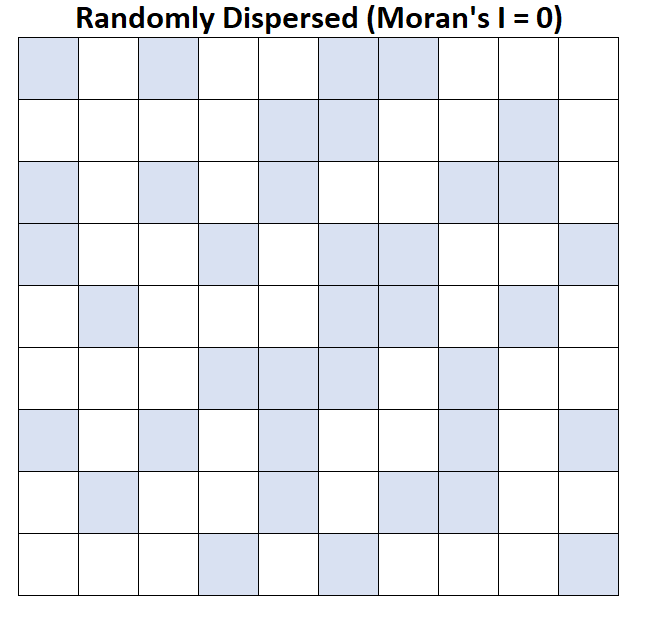
मोरन का I = -1: औसत घरेलू आय पूरी तरह से बिखरी हुई है।

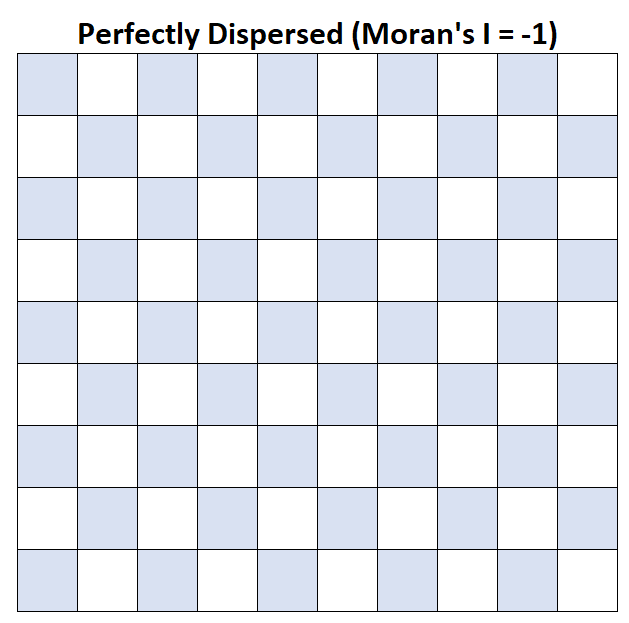
मोरन का I = 1: औसत घरेलू आय पूरी तरह से समूहीकृत है।

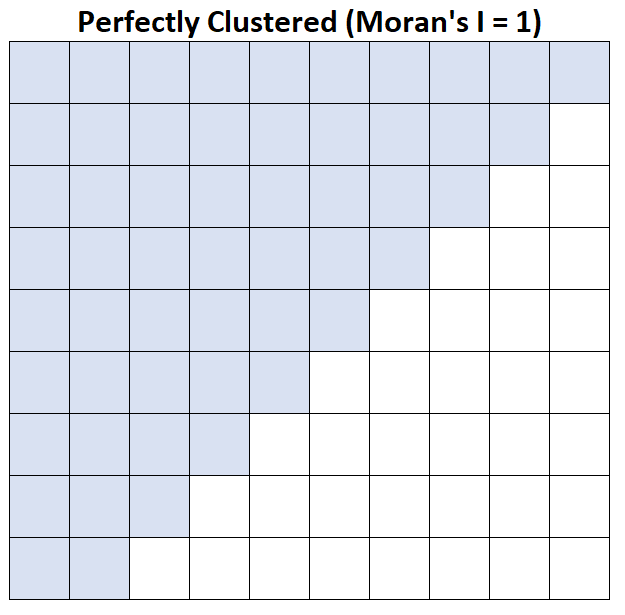
सांख्यिकीय सॉफ्टवेयर आर में मोरन के I की गणना के एक ठोस उदाहरण के लिए इस उदाहरण को देखें।