येट निरंतरता सुधार: परिभाषा और उदाहरण

स्वतंत्रता के काई-स्क्वायर परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि दो श्रेणीगत चरों के बीच कोई महत्वपूर्ण संबंध है या नहीं।

यह परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

• एच ₀ : (शून्य परिकल्पना) दो चर स्वतंत्र हैं।
• एच ₁ : (वैकल्पिक परिकल्पना) दो चर स्वतंत्र नहीं हैं। (अर्थात् वे संबद्ध हैं)

इस परीक्षण के लिए ची-स्क्वायर x ² परीक्षण आँकड़ा की गणना करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:

एक्स ² = Σ(ओ _आई -ई _आई ) ² / ई _आई

सोना:

• Σ: एक फैंसी प्रतीक है जिसका अर्थ है “योग”
• ओ: मनाया गया मूल्य
• ई: अपेक्षित मूल्य

यह परीक्षण मानता है कि आकस्मिक तालिका में आवृत्तियों की अलग-अलग संभावनाओं का अनुमान ची-स्क्वायर वितरण द्वारा लगाया जा सकता है, जो एक सतत वितरण है।

हालाँकि, यह धारणा थोड़ी गलत होती है और परिणामी परीक्षण आँकड़े ऊपर की ओर झुके होते हैं।

इस पूर्वाग्रह को ठीक करने के लिए, हम येट के निरंतरता सुधार को लागू कर सकते हैं, जो सूत्र ^X2 में निम्नलिखित सुधार को लागू करता है:

एक्स ² = Σ(|ओ _आई -ई _आई | – 0.5) ² / ई _आई

हम आम तौर पर इस सुधार का उपयोग केवल तभी करते हैं जब आकस्मिकता तालिका में कम से कम एक सेल की अपेक्षित आवृत्ति 5 से कम हो।

उदाहरण: येट की निरंतरता सुधार का अनुप्रयोग

मान लीजिए हम जानना चाहते हैं कि किसी राजनीतिक दल की प्राथमिकता के साथ लिंग का संबंध है या नहीं। हम 40 मतदाताओं का एक सरल यादृच्छिक नमूना लेते हैं और उनसे उनकी राजनीतिक पार्टी की पसंद के बारे में पूछते हैं। निम्नलिखित तालिका सर्वेक्षण के परिणाम प्रस्तुत करती है:

येट की निरंतरता सुधार के साथ स्वतंत्रता का ची-स्क्वायर परीक्षण करने का तरीका यहां बताया गया है:

देखे गए मान:

अपेक्षित मूल्य:

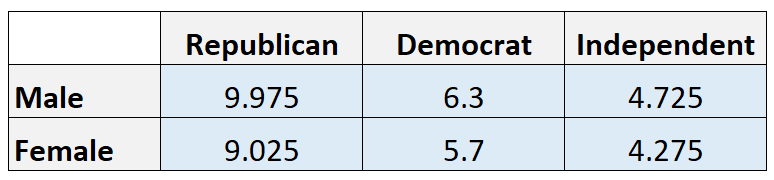
नोट: हम पंक्ति के कुल को कॉलम के कुल से गुणा करके और फिर कुल योग से विभाजित करके प्रत्येक सेल में अपेक्षित मान की गणना करते हैं। उदाहरण के लिए, रिपब्लिकन पुरुषों की अपेक्षित संख्या (21*19)/40 = 9.975 है।

^{ची –} _{वर्ग परीक्षण आँकड़ा} :

• (|8-9.975| – 0.5) ² / 9.975 = 0.218
• (|9-6.3| – 0.5) ² / 6.3 = 0.768
• (|4-4.725| – 0.5) ² / 4.725 = 0.011
• (|11-9.025| – 0.5) ² / 9.025 = 0.241
• (|3-5.7| – 0.5) ² / 5.7 = 0.849
• (|5-4.275| – 0.5) ² / 4.275 = 0.012

^तो ,

पी-वैल्यू: ची-स्क्वायर से पी-वैल्यू कैलकुलेटर के अनुसार, पी-वैल्यू जो 2 डिग्री स्वतंत्रता के साथ ची-स्क्वायर परीक्षण आंकड़े से मेल खाता है, 0.3501 है।

चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहेंगे। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि लिंग और राजनीतिक दल की प्राथमिकताओं के बीच कोई संबंध है।