रिज रिग्रेशन का परिचय

सामान्य एकाधिक रैखिक प्रतिगमन में, हम फॉर्म के एक मॉडल को फिट करने के लिए पी भविष्यवक्ता चर और एक प्रतिक्रिया चर का एक सेट का उपयोग करते हैं:

वाई = β ₀ + β ₁ एक्स _{1 +} β ₂ एक्स ₂ + … + β _पी

सोना:

• Y : प्रतिक्रिया चर
• एक्स _जे : जे ^वें पूर्वानुमानित चर
• β _जे : एक्स _जे में एक इकाई की वृद्धि का वाई पर औसत प्रभाव, अन्य सभी भविष्यवक्ताओं को स्थिर रखता है
• ε : त्रुटि पद

β ₀ , β ₁ , B ₂ , …, β _p का मान न्यूनतम वर्ग विधि का उपयोग करके चुना जाता है, जो अवशेषों (RSS) के वर्गों के योग को कम करता है:

आरएसएस = Σ(y _i – ŷ _i ) ²

सोना:

• Σ : एक ग्रीक प्रतीक जिसका अर्थ है योग
• y _i : ^iवें अवलोकन के लिए वास्तविक प्रतिक्रिया मान
• ŷ _i : एकाधिक रेखीय प्रतिगमन मॉडल के आधार पर अनुमानित प्रतिक्रिया मूल्य

हालाँकि, जब भविष्यवक्ता चर अत्यधिक सहसंबद्ध होते हैं, तो बहुसंरेखता एक समस्या बन सकती है। यह मॉडल गुणांक अनुमानों को अविश्वसनीय बना सकता है और उच्च विचरण प्रदर्शित कर सकता है।

मॉडल से कुछ भविष्यवक्ता चर को पूरी तरह से हटाए बिना इस समस्या से निपटने का एक तरीका रिज रिग्रेशन नामक विधि का उपयोग करना है, जो इसके बजाय निम्नलिखित को कम करना चाहता है:

आरएसएस + λΣβ _जे ²

जहां j 1 से p और λ ≥ 0 तक जाता है।

समीकरण में इस दूसरे पद को निकासी दंड के रूप में जाना जाता है।

जब λ = 0, इस दंड शब्द का कोई प्रभाव नहीं पड़ता है और रिज प्रतिगमन न्यूनतम वर्गों के समान गुणांक अनुमान उत्पन्न करता है। हालाँकि, जैसे-जैसे λ अनंत तक पहुंचता है, सिकुड़न दंड अधिक प्रभावशाली हो जाता है और शिखर प्रतिगमन गुणांक अनुमान शून्य के करीब पहुंच जाता है।

सामान्य तौर पर, मॉडल में सबसे कम प्रभावशाली भविष्यवक्ता चर सबसे तेजी से शून्य की ओर गिरेंगे।

रिज रिग्रेशन का उपयोग क्यों करें?

न्यूनतम वर्ग प्रतिगमन की तुलना में रिज प्रतिगमन का लाभ पूर्वाग्रह-विचरण ट्रेडऑफ़ है।

याद रखें कि मीन स्क्वायर एरर (एमएसई) एक मीट्रिक है जिसका उपयोग हम किसी दिए गए मॉडल की सटीकता को मापने के लिए कर सकते हैं और इसकी गणना निम्नानुसार की जाती है:

एमएसई = वार( एफ̂( एक्स ₀ )) + [पूर्वाग्रह( एफ̂( एक्स ₀ ))] ² + वार(ε)

एमएसई = वेरिएंस + बायस ² + इरेड्यूसबल त्रुटि

रिज रिग्रेशन का मूल विचार एक छोटा पूर्वाग्रह पेश करना है ताकि विचरण को काफी कम किया जा सके, जिससे समग्र एमएसई कम हो।

इसे स्पष्ट करने के लिए, निम्नलिखित ग्राफ़ पर विचार करें:

ध्यान दें कि जैसे-जैसे λ बढ़ता है, पूर्वाग्रह में बहुत कम वृद्धि के साथ विचरण काफी कम हो जाता है। हालाँकि, एक निश्चित बिंदु से परे, विचरण कम तेजी से घटता है और गुणांकों में कमी से उनका महत्वपूर्ण कम आकलन होता है, जिससे पूर्वाग्रह में तेज वृद्धि होती है।

हम ग्राफ़ से देख सकते हैं कि परीक्षण का एमएसई सबसे कम है जब हम λ के लिए एक मान चुनते हैं जो पूर्वाग्रह और भिन्नता के बीच एक इष्टतम व्यापार-बंद उत्पन्न करता है।

जब λ = 0, रिज रिग्रेशन में दंड शब्द का कोई प्रभाव नहीं पड़ता है और इसलिए कम से कम वर्गों के समान गुणांक अनुमान उत्पन्न होता है। हालाँकि, λ को एक निश्चित बिंदु तक बढ़ाकर, हम परीक्षण के समग्र MSE को कम कर सकते हैं।

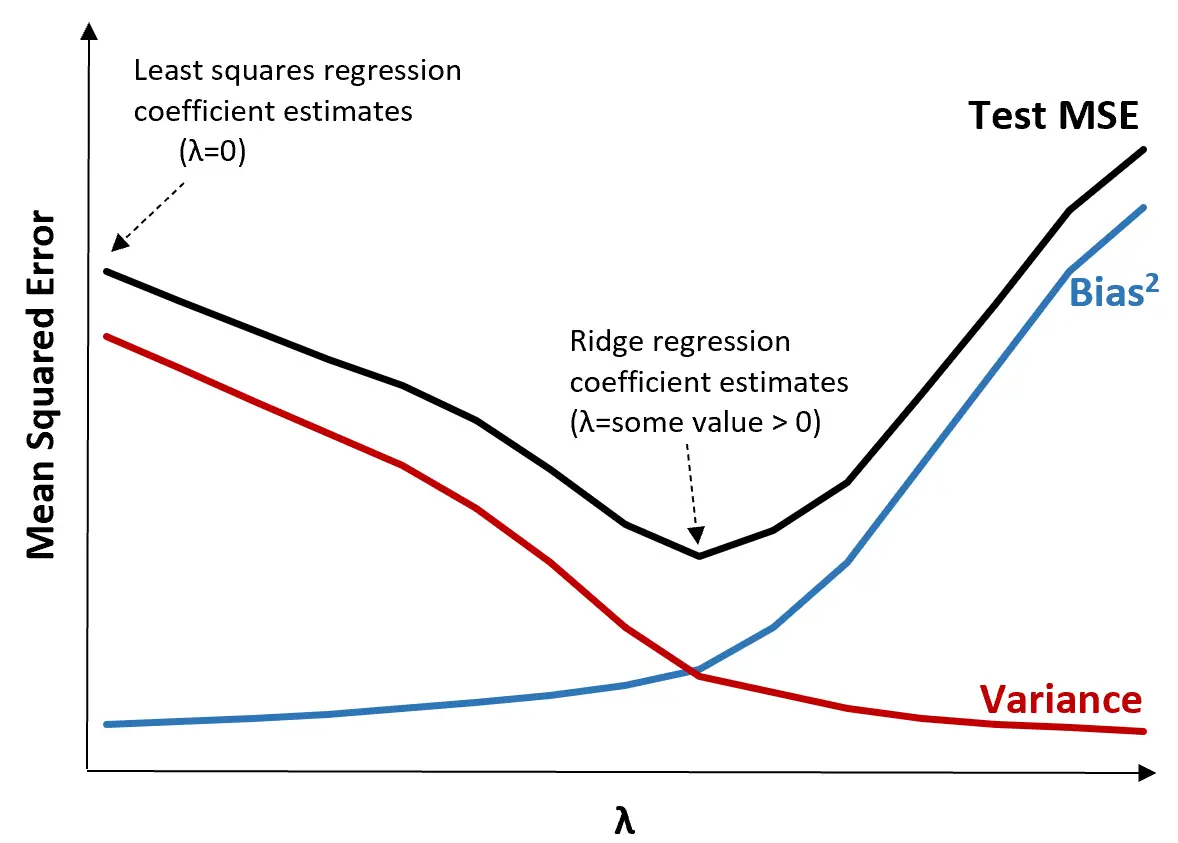
इसका मतलब यह है कि रिज रिग्रेशन द्वारा मॉडल फिटिंग कम से कम वर्ग रिग्रेशन द्वारा मॉडल फिटिंग की तुलना में छोटी परीक्षण त्रुटियां उत्पन्न करेगी।

अभ्यास में रिज रिग्रेशन करने के चरण

रिज रिग्रेशन करने के लिए निम्नलिखित चरणों का उपयोग किया जा सकता है:

चरण 1: भविष्यवक्ता चर के लिए सहसंबंध मैट्रिक्स और वीआईएफ मानों की गणना करें।

सबसे पहले, हमें एक सहसंबंध मैट्रिक्स तैयार करने और प्रत्येक भविष्यवक्ता चर के लिए वीआईएफ (विचरण मुद्रास्फीति कारक) मूल्यों की गणना करने की आवश्यकता है।

यदि हम भविष्यवक्ता चर और उच्च वीआईएफ मानों के बीच एक मजबूत सहसंबंध का पता लगाते हैं (कुछ पाठ “उच्च” वीआईएफ मान को 5 के रूप में परिभाषित करते हैं जबकि अन्य 10 का उपयोग करते हैं), तो रिज रिग्रेशन संभवतः उपयुक्त है।

हालाँकि, यदि डेटा में कोई बहुसंरेखता नहीं है, तो पहले स्थान पर रिज रिग्रेशन करना आवश्यक नहीं हो सकता है। इसके बजाय, हम सामान्य न्यूनतम वर्ग प्रतिगमन निष्पादित कर सकते हैं।

चरण 2: प्रत्येक भविष्यवक्ता चर को मानकीकृत करें।

रिज रिग्रेशन करने से पहले, हमें डेटा को इस तरह स्केल करने की आवश्यकता है कि प्रत्येक प्रेडिक्टर वेरिएबल का माध्य 0 और मानक विचलन 1 हो। यह सुनिश्चित करता है कि रिज रिग्रेशन चलाते समय किसी भी प्रेडिक्टर वेरिएबल का अत्यधिक प्रभाव न हो।

चरण 3: रिज रिग्रेशन मॉडल को फिट करें और λ के लिए एक मान चुनें।

ऐसा कोई सटीक सूत्र नहीं है जिसका उपयोग हम यह निर्धारित करने के लिए कर सकें कि λ के लिए किस मान का उपयोग किया जाए। व्यवहार में, λ चुनने के दो सामान्य तरीके हैं:

(1) एक रिज ट्रेस प्लॉट बनाएं। यह एक ग्राफ़ है जो अनंत की ओर बढ़ने पर गुणांक अनुमान के मूल्यों की कल्पना करता है। आमतौर पर, हम λ को उस मान के रूप में चुनते हैं जिस पर अधिकांश गुणांक अनुमान स्थिर होने लगते हैं।

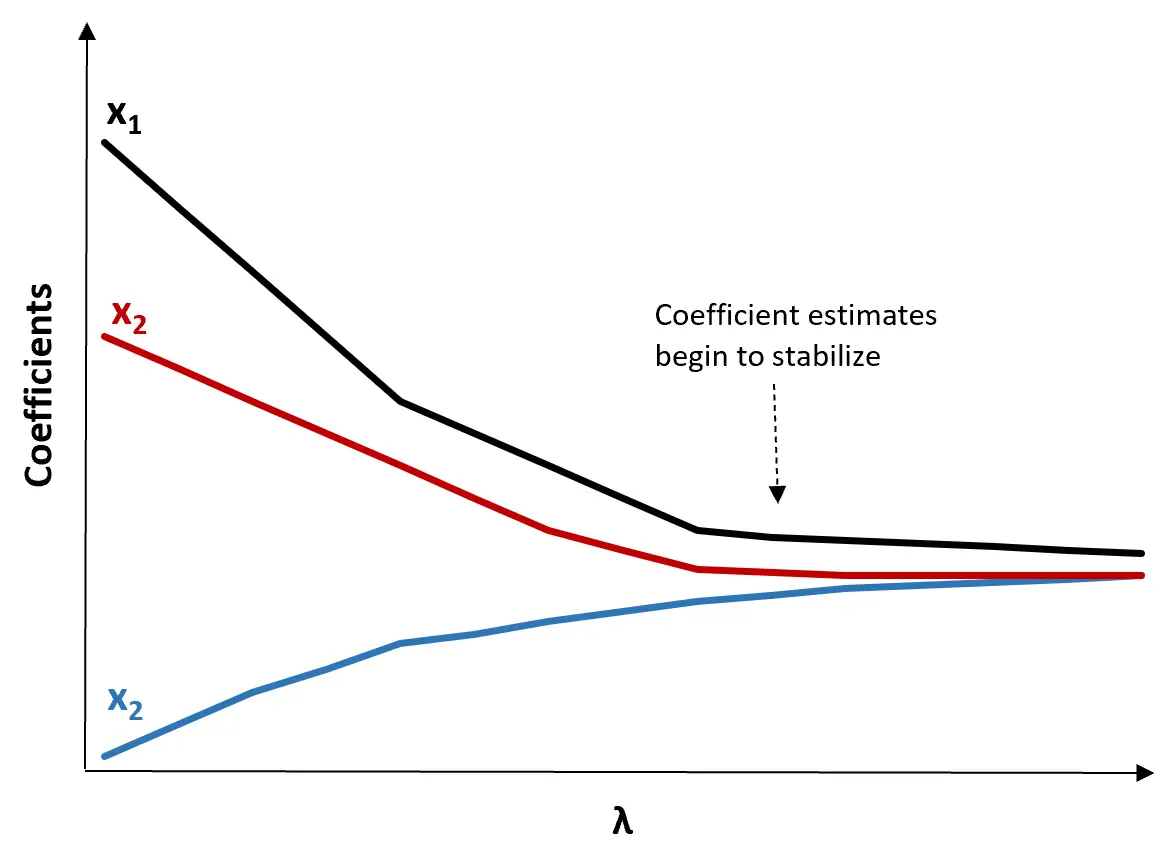
(2) λ के प्रत्येक मान के लिए एमएसई परीक्षण की गणना करें।

λ चुनने का दूसरा तरीका यह है कि λ के विभिन्न मूल्यों के साथ प्रत्येक मॉडल के परीक्षण MSE की गणना करें और λ को वह मान चुनें जो सबसे कम परीक्षण MSE उत्पन्न करता है।

रिज रिग्रेशन के फायदे और नुकसान

रिज रिग्रेशन का सबसे बड़ा लाभ मल्टीकोलाइनरिटी मौजूद होने पर न्यूनतम वर्गों की तुलना में कम परीक्षण माध्य वर्ग त्रुटि (एमएसई) उत्पन्न करने की क्षमता है।

हालाँकि, रिज रिग्रेशन का सबसे बड़ा दोष इसकी चर चयन करने में असमर्थता है क्योंकि इसमें अंतिम मॉडल में सभी भविष्यवक्ता चर शामिल हैं। चूँकि कुछ भविष्यवक्ता शून्य के बहुत करीब आ जाएंगे, इससे मॉडल परिणामों की व्याख्या करना मुश्किल हो सकता है।

व्यवहार में, रिज रिग्रेशन में एक ऐसा मॉडल तैयार करने की क्षमता है जो कम से कम वर्ग मॉडल की तुलना में बेहतर भविष्यवाणियां करने में सक्षम है, लेकिन मॉडल के परिणामों की व्याख्या करना अक्सर अधिक कठिन होता है।

इस पर निर्भर करते हुए कि मॉडल व्याख्या या पूर्वानुमान सटीकता आपके लिए अधिक महत्वपूर्ण है, आप विभिन्न परिदृश्यों में सामान्य न्यूनतम वर्ग या रिज प्रतिगमन का उपयोग करना चुन सकते हैं।

आर और पायथन में रिज रिग्रेशन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर और पायथन में रिज रिग्रेशन कैसे करें, रिज रिग्रेशन मॉडल फिट करने के लिए दो सबसे अधिक इस्तेमाल की जाने वाली भाषाएँ:

आर में रिज रिग्रेशन (कदम दर कदम)
पायथन में रिज रिग्रेशन (कदम दर कदम)