लघुगणक प्रतिगमन

यह आलेख बताता है कि लॉगरिदमिक प्रतिगमन क्या है और यह कैसे किया जाता है। इसके अतिरिक्त, आप अवधारणा को पूरी तरह से समझने के लिए लॉगरिदमिक प्रतिगमन का एक उदाहरण देख सकते हैं।

लघुगणक प्रतिगमन क्या है?

लघुगणक प्रतिगमन एक प्रतिगमन मॉडल है जिसमें इसके समीकरण में एक लघुगणक शामिल होता है। विशेष रूप से, लघुगणक प्रतिगमन में, स्वतंत्र चर का लघुगणक लिया जाता है। तो लघुगणक प्रतिगमन मॉडल के लिए समीकरण y=a+b·ln(x) है।

जब नमूना डेटा एक लघुगणकीय वक्र बनाता है, तो प्रतिगमन मॉडल को फिट करने के लिए लॉगरिदमिक प्रतिगमन बहुत उपयोगी होता है, ताकि प्रतिगमन मॉडल नमूना डेटा को बेहतर ढंग से फिट कर सके। नीचे हम देखेंगे कि आपको लघुगणक प्रतिगमन कब करना चाहिए।

इस प्रकार, लघुगणक प्रतिगमन एक प्रकार का अरेखीय प्रतिगमन है, ठीक घातीय प्रतिगमन और बहुपद प्रतिगमन की तरह।

लघुगणक प्रतिगमन सूत्र

एक लघुगणकीय प्रतिगमन मॉडल में स्वतंत्र चर का लघुगणक लेना शामिल होता है। इसलिए, लघुगणक प्रतिगमन के समीकरण का सूत्र y=a+b·ln(x) है।

सोना:

• 

  आश्रित चर है.

• 

  स्वतंत्र चर है.

• 

  प्रतिगमन गुणांक हैं.

ध्यान दें कि y=a+b·ln(x) वास्तव में एक रेखा का समीकरण है, लेकिन मूल चर x और y को संदर्भित करने के बजाय, यह चर ln(x) और y को संदर्भित करता है।

लघुगणकीय प्रतिगमन कब करें?

जब नमूना डेटा का ग्राफ़ एक लॉगरिदमिक वक्र होता है, यानी, जब बिंदुओं का प्लॉट लॉगरिदमिक फ़ंक्शन के ग्राफ़ के समान होता है, तो हमें लॉगरिदमिक प्रतिगमन करने की आवश्यकता होती है।

नीचे दिए गए स्कैटरप्लॉट को देखें, एक रैखिक प्रतिगमन मॉडल को डेटासेट में फिट किया गया था। जैसा कि आप देख सकते हैं, रेखा डेटा का खराब अनुमान नहीं है, हालांकि, यदि आप सावधान रहें, तो अंत की तुलना में ग्राफ़ की शुरुआत में मान अधिक तेजी से बढ़ते हैं, इसलिए रेखा पूरी तरह से टिप्पणियों से मेल नहीं खाती है .

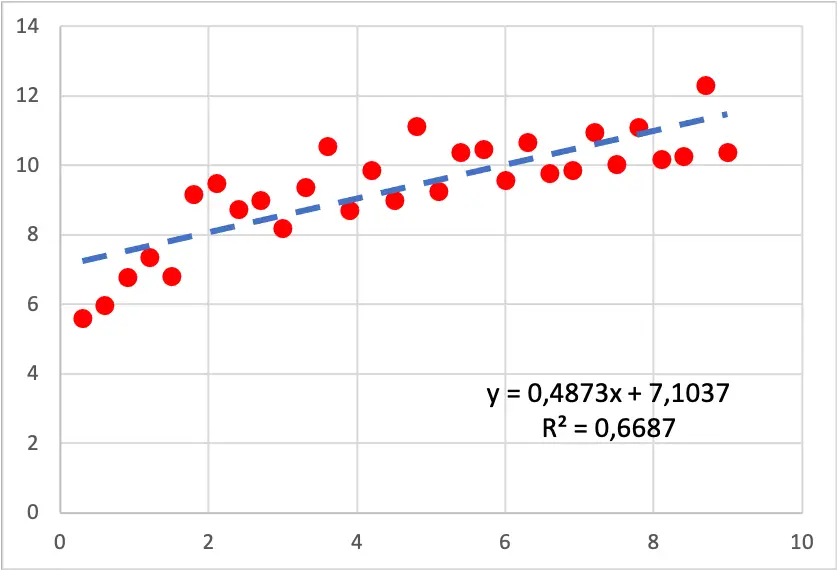
इसलिए एक लघुगणक प्रतिगमन मॉडल बनाने का प्रयास करना उचित है, क्योंकि ऐसा लगता है कि डेटा एक लघुगणकीय वक्र का अनुसरण करता है। लघुगणक प्रतिगमन मॉडल से प्राप्त परिणाम इस प्रकार है:

जैसा कि आप पिछले ग्राफ़ में देख सकते हैं, परिणामी लघुगणक प्रतिगमन मॉडल नमूना डेटा को बेहतर ढंग से फिट करता है। वास्तव में, निर्धारण का गुणांक 66.87% से बढ़कर 80.05% हो गया है, इसलिए मॉडल अब डेटा नमूने को बेहतर ढंग से समझा सकता है। इसलिए, इस मामले में, डेटा मान का अनुमान लगाने वाले समीकरण को खोजने के लिए लॉजिस्टिक रिग्रेशन का उपयोग करना बेहतर है।

अन्य प्रकार के अरेखीय प्रतिगमन

अरेखीय प्रतिगमन के तीन सबसे आम मामले हैं:

• लघुगणक प्रतिगमन : स्वतंत्र चर का लघुगणक लिया जाता है।
• घातीय प्रतिगमन : स्वतंत्र चर समीकरण का घातांक है।
• बहुपद प्रतिगमन : प्रतिगमन मॉडल समीकरण एक बहुपद के रूप में है।