संभार तन्त्र परावर्तन
यह आलेख बताता है कि आंकड़ों में लॉजिस्टिक रिग्रेशन क्या है। इसी तरह, आपको लॉजिस्टिक रिग्रेशन फॉर्मूला मिलेगा, लॉजिस्टिक रिग्रेशन के विभिन्न प्रकार क्या हैं और, इसके अलावा, एक हल किया गया लॉजिस्टिक रिग्रेशन अभ्यास भी मिलेगा।
लॉजिस्टिक रिग्रेशन क्या है?
आंकड़ों में, लॉजिस्टिक रिग्रेशन एक प्रकार का रिग्रेशन मॉडल है जिसका उपयोग श्रेणीबद्ध चर के परिणाम की भविष्यवाणी करने के लिए किया जाता है। अर्थात्, लॉजिस्टिक रिग्रेशन का उपयोग इस संभावना को मॉडल करने के लिए किया जाता है कि एक श्रेणीगत चर स्वतंत्र चर के आधार पर एक निश्चित मान लेता है।
सबसे आम लॉजिस्टिक रिग्रेशन मॉडल बाइनरी लॉजिस्टिक रिग्रेशन है, जिसमें केवल दो संभावित परिणाम होते हैं: “विफलता” या “सफलता” ( बर्नौली वितरण )। “असफलता” को मान 0 द्वारा दर्शाया जाता है, जबकि “सफलता” को मान 1 द्वारा दर्शाया जाता है।
उदाहरण के लिए, एक छात्र द्वारा पढ़ाई में बिताए गए घंटों के आधार पर परीक्षा उत्तीर्ण करने की संभावना का अध्ययन लॉजिस्टिक रिग्रेशन मॉडल का उपयोग करके किया जा सकता है। इस मामले में, विफलता “विफलता” का परिणाम होगी और दूसरी ओर, सफलता “सफलता” का परिणाम होगी।
लॉजिस्टिक रिग्रेशन फॉर्मूला
लॉजिस्टिक रिग्रेशन मॉडल के लिए समीकरण है:
![]()
इसलिए, एक लॉजिस्टिक रिग्रेशन मॉडल में, “सफलता” परिणाम प्राप्त करने की संभावना, यानी कि आश्रित चर मान 1 लेता है, की गणना निम्न सूत्र से की जाती है:
![]()
सोना:
-

संभावना है कि आश्रित चर 1 है।
-

लॉजिस्टिक रिग्रेशन मॉडल का स्थिरांक है।
-

चर i का प्रतिगमन गुणांक है।
-

चर i का मान है.
लॉजिस्टिक रिग्रेशन मॉडल उदाहरण
अब जब हम लॉजिस्टिक रिग्रेशन की परिभाषा जानते हैं, तो आइए इस प्रकार के रिग्रेशन का एक मॉडल कैसे बनाएं इसका एक ठोस उदाहरण देखें।
- निम्नलिखित तालिका में, डेटा के 20 टुकड़ों की एक श्रृंखला संकलित की गई है जो प्रत्येक छात्र के अध्ययन के घंटों से संबंधित है और चाहे वे सांख्यिकी परीक्षा में उत्तीर्ण हुए हों या असफल। एक लॉजिस्टिक रिग्रेशन मॉडल चलाएं और इस संभावना की गणना करें कि यदि कोई छात्र 4 घंटे पढ़ाई करता है तो वह पास हो जाएगा।
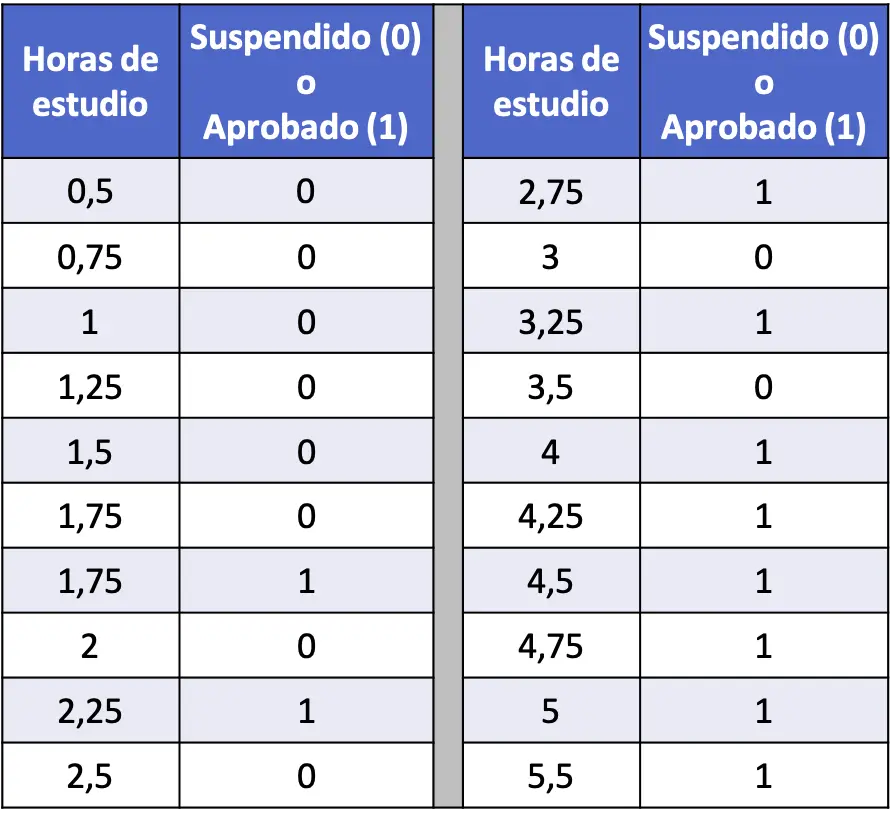
इस मामले में, व्याख्यात्मक चर अध्ययन के घंटों की संख्या है और प्रतिक्रिया चर यह है कि क्या छात्र असफल (0) या उत्तीर्ण (1) है। इसलिए, हमारे मॉडल में हमारे पास केवल गुणांक होगा
![]()
और गुणांक
![]()
, चूँकि केवल एक स्वतंत्र चर है।
![]()
प्रतिगमन गुणांक का मैन्युअल निर्धारण बहुत श्रमसाध्य है, इसलिए मिनिटैब जैसे कंप्यूटर सॉफ़्टवेयर का उपयोग करने की अनुशंसा की जाती है। इस प्रकार, मिनिटैब का उपयोग करके गणना किए गए प्रतिगमन गुणांक के मान इस प्रकार हैं:
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
इसलिए लॉजिस्टिक रिग्रेशन मॉडल इस प्रकार है:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
नीचे आप नमूना डेटा और लॉजिस्टिक रिग्रेशन मॉडल समीकरण का रेखांकन देख सकते हैं:
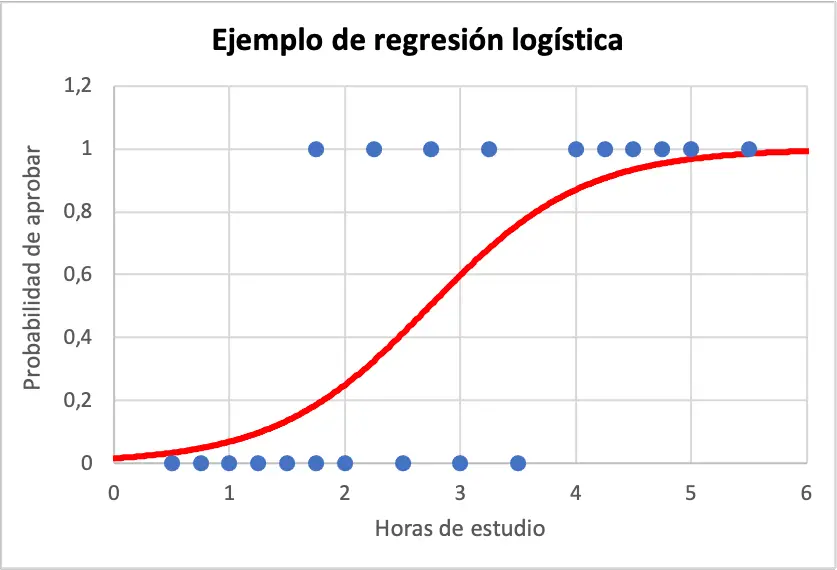
इस प्रकार, इस संभावना की गणना करने के लिए कि यदि एक छात्र ने 4 घंटे अध्ययन किया है तो वह सफल होगा, बस लॉजिस्टिक रिग्रेशन मॉडल से प्राप्त समीकरण का उपयोग करें:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
संक्षेप में, यदि कोई छात्र चार घंटे पढ़ाई करता है, तो उसके परीक्षा उत्तीर्ण करने की संभावना 86.99% होगी।
लॉजिस्टिक रिग्रेशन के प्रकार
लॉजिस्टिक रिग्रेशन तीन प्रकार के होते हैं:
- बाइनरी लॉजिस्टिक रिग्रेशन : आश्रित चर के केवल दो मान (0 और 1) हो सकते हैं।
- मल्टीनोमियल लॉजिस्टिक रिग्रेशन : आश्रित चर के दो से अधिक संभावित मान होते हैं।
- सामान्य लॉजिस्टिक प्रतिगमन : संभावित परिणामों का एक प्राकृतिक क्रम होता है।
लॉजिस्टिक रिग्रेशन और लीनियर रिग्रेशन
अंत में, संक्षेप में, हम देखेंगे कि लॉजिस्टिक रिग्रेशन और लीनियर रिग्रेशन के बीच क्या अंतर है, क्योंकि आंकड़ों में सबसे अधिक इस्तेमाल किया जाने वाला रिग्रेशन मॉडल लीनियर मॉडल है।
रैखिक प्रतिगमन का उपयोग संख्यात्मक निर्भर चर को मॉडल करने के लिए किया जाता है। इसके अतिरिक्त, रैखिक प्रतिगमन में, व्याख्यात्मक चर और प्रतिक्रिया चर के बीच संबंध रैखिक होता है।
इसलिए, लॉजिस्टिक रिग्रेशन और लीनियर रिग्रेशन के बीच मुख्य अंतर आश्रित चर का प्रकार है। लॉजिस्टिक रिग्रेशन में, आश्रित चर श्रेणीबद्ध होता है, जबकि रैखिक रिग्रेशन में आश्रित चर संख्यात्मक होता है।
इस प्रकार, लॉजिस्टिक रिग्रेशन का उपयोग दो संभावित विकल्पों के बीच परिणाम की भविष्यवाणी करने के लिए किया जाता है, जबकि रैखिक रिग्रेशन एक संख्यात्मक परिणाम की भविष्यवाणी करने में मदद करता है।