पायथन में लॉजिस्टिक रिग्रेशन कैसे करें (चरण दर चरण)

लॉजिस्टिक रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम रिग्रेशन मॉडल को फिट करने के लिए कर सकते हैं जब प्रतिक्रिया चर द्विआधारी होता है।

लॉजिस्टिक रिग्रेशन निम्नलिखित रूप का समीकरण खोजने के लिए अधिकतम संभावना अनुमान के रूप में ज्ञात विधि का उपयोग करता है:

लॉग[पी(एक्स) / ( ₁ -पी(एक्स))] = β ₀ + β ₁ एक्स ₁ + β ₂ एक्स ₂ + … + β _पी

सोना:

• एक्स _जे : जे ^वें पूर्वानुमानित चर
• β _j : j ^वें पूर्वानुमानित चर के लिए गुणांक का अनुमान

समीकरण के दाईं ओर का सूत्र लॉग ऑड्स की भविष्यवाणी करता है कि प्रतिक्रिया चर मान 1 लेता है।

इसलिए, जब हम एक लॉजिस्टिक रिग्रेशन मॉडल को फिट करते हैं, तो हम इस संभावना की गणना करने के लिए निम्नलिखित समीकरण का उपयोग कर सकते हैं कि किसी दिए गए अवलोकन का मान 1 है:

पी(एक्स) = ई ^{β ₀ + _{β 1 एक्स 1 + β 2 एक्स 2 + … + β}} पी

फिर हम अवलोकन को 1 या 0 के रूप में वर्गीकृत करने के लिए एक निश्चित संभाव्यता सीमा का उपयोग करते हैं।

उदाहरण के लिए, हम कह सकते हैं कि 0.5 से अधिक या उसके बराबर संभावना वाले अवलोकनों को “1” के रूप में वर्गीकृत किया जाएगा और अन्य सभी अवलोकनों को “0” के रूप में वर्गीकृत किया जाएगा।

यह ट्यूटोरियल आर में लॉजिस्टिक रिग्रेशन कैसे करें इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: आवश्यक पैकेज आयात करें

सबसे पहले, हम पायथन में लॉजिस्टिक रिग्रेशन करने के लिए आवश्यक पैकेज आयात करेंगे:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

चरण 2: डेटा लोड करें

इस उदाहरण के लिए, हम इंट्रोडक्शन टू स्टैटिस्टिकल लर्निंग पुस्तक से डिफ़ॉल्ट डेटासेट का उपयोग करेंगे। हम डेटासेट का सारांश लोड करने और प्रदर्शित करने के लिए निम्नलिखित कोड का उपयोग कर सकते हैं:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

इस डेटासेट में 10,000 व्यक्तियों के बारे में निम्नलिखित जानकारी शामिल है:

• डिफ़ॉल्ट: इंगित करता है कि किसी व्यक्ति ने डिफ़ॉल्ट किया है या नहीं।
• छात्र: इंगित करता है कि कोई व्यक्ति छात्र है या नहीं।
• शेष: किसी व्यक्ति द्वारा रखा गया औसत शेष।
• आय: व्यक्ति की आय.

हम एक लॉजिस्टिक रिग्रेशन मॉडल बनाने के लिए छात्र की स्थिति, बैंक बैलेंस और आय का उपयोग करेंगे जो इस संभावना की भविष्यवाणी करता है कि कोई व्यक्ति डिफ़ॉल्ट होगा।

चरण 3: प्रशिक्षण और परीक्षण नमूने बनाएं

इसके बाद, हम मॉडल को प्रशिक्षित करने के लिए डेटासेट को एक प्रशिक्षण सेट और मॉडल का परीक्षण करने के लिए एक परीक्षण सेट में विभाजित करेंगे।

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

चरण 4: लॉजिस्टिक रिग्रेशन मॉडल को फिट करें

इसके बाद, हम लॉजिस्टिक रिग्रेशन मॉडल को डेटासेट में फिट करने के लिए लॉजिस्टिक रिग्रेशन() फ़ंक्शन का उपयोग करेंगे:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

चरण 5: मॉडल डायग्नोस्टिक्स

एक बार जब हम प्रतिगमन मॉडल फिट कर लेते हैं, तो हम परीक्षण डेटासेट पर अपने मॉडल के प्रदर्शन का विश्लेषण कर सकते हैं।

सबसे पहले, हम मॉडल के लिए भ्रम मैट्रिक्स बनाएंगे :

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

भ्रम मैट्रिक्स से हम देख सकते हैं कि:

• #सच्ची सकारात्मक भविष्यवाणियाँ: 2886
• #सच्ची नकारात्मक भविष्यवाणियाँ: 0
• #झूठी सकारात्मक भविष्यवाणियाँ: 113
• #गलत नकारात्मक भविष्यवाणियाँ: 1

हम सटीकता मॉडल भी प्राप्त कर सकते हैं, जो हमें मॉडल द्वारा किए गए सुधार पूर्वानुमानों का प्रतिशत बताता है:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

यह हमें बताता है कि मॉडल ने इस बारे में सही भविष्यवाणी की है कि कोई व्यक्ति 96.2% समय डिफॉल्ट करेगा या नहीं।

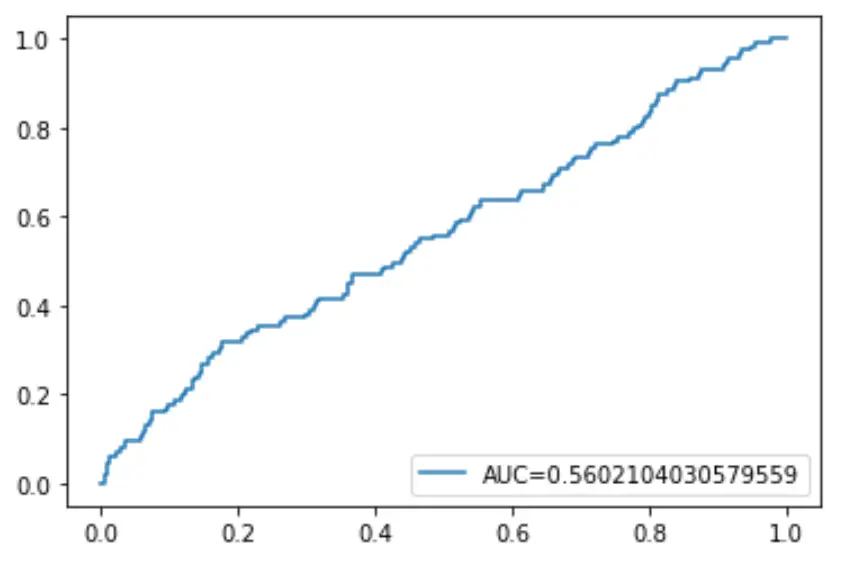
अंत में, हम रिसीवर ऑपरेटिंग कैरेक्टरिस्टिक (आरओसी) वक्र को प्लॉट कर सकते हैं जो मॉडल द्वारा अनुमानित वास्तविक सकारात्मकता का प्रतिशत प्रदर्शित करता है जब भविष्यवाणी संभावना सीमा 1 से 0 तक कम हो जाती है।

AUC (वक्र के नीचे का क्षेत्र) जितना अधिक होगा, हमारा मॉडल उतना ही सटीक रूप से परिणामों की भविष्यवाणी करने में सक्षम होगा:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()