वक्रीय प्रतिगमन क्या है? (परिभाषा एवं उदाहरण)

वक्ररेखीय प्रतिगमन किसी भी प्रतिगमन मॉडल को दिया गया नाम है जो एक सीधी रेखा के बजाय एक वक्र को फिट करने का प्रयास करता है।

वक्रीय प्रतिगमन मॉडल के सामान्य उदाहरणों में शामिल हैं:

द्विघात प्रतिगमन: इसका उपयोग तब किया जाता है जब एक पूर्वसूचक चर और एक प्रतिक्रिया चर के बीच एक द्विघात संबंध मौजूद होता है। जब रेखांकन किया जाता है, तो इस प्रकार का संबंध स्कैटरप्लॉट पर “यू” या उल्टे “यू” जैसा दिखता है:

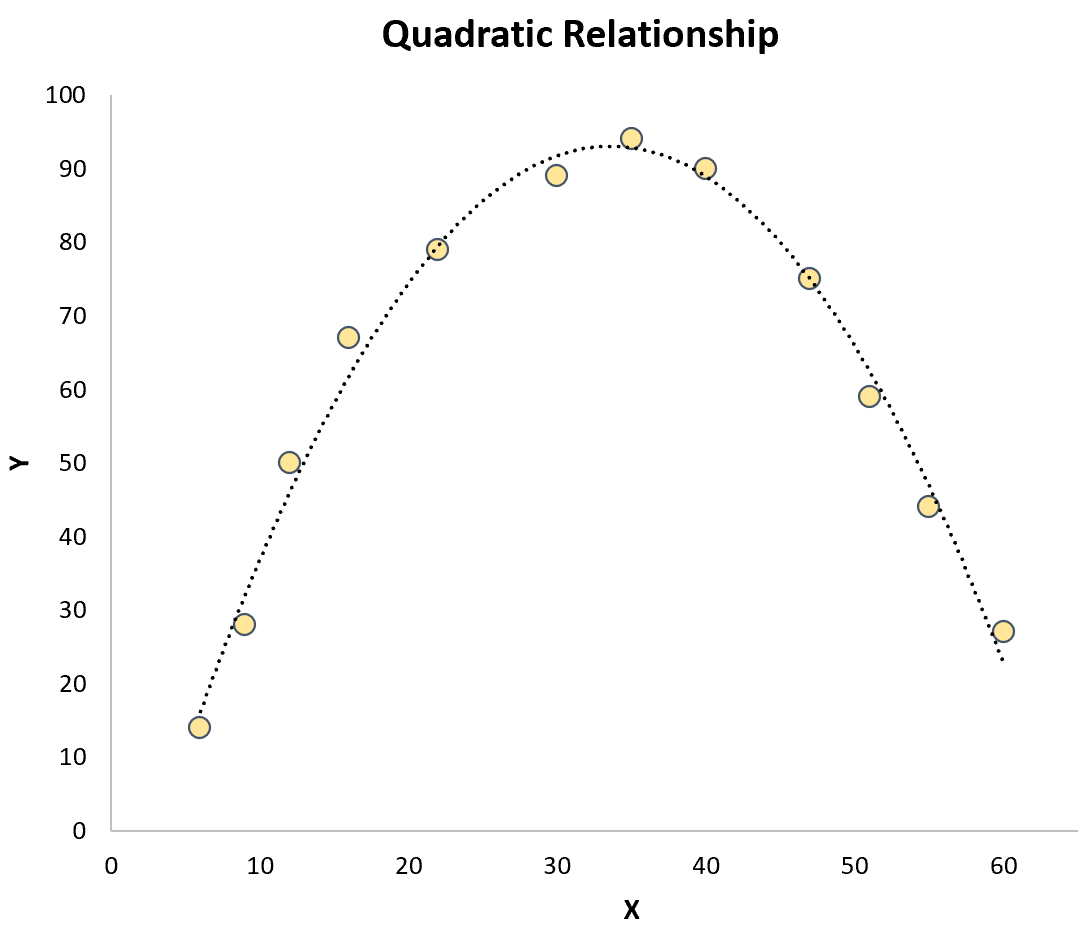
क्यूबिक रिग्रेशन: इसका उपयोग तब किया जाता है जब एक पूर्वानुमानक चर और एक प्रतिक्रिया चर के बीच एक घन संबंध मौजूद होता है। जब रेखांकन किया जाता है, तो इस प्रकार का संबंध स्कैटरप्लॉट पर दो अलग-अलग वक्र दिखाता है:

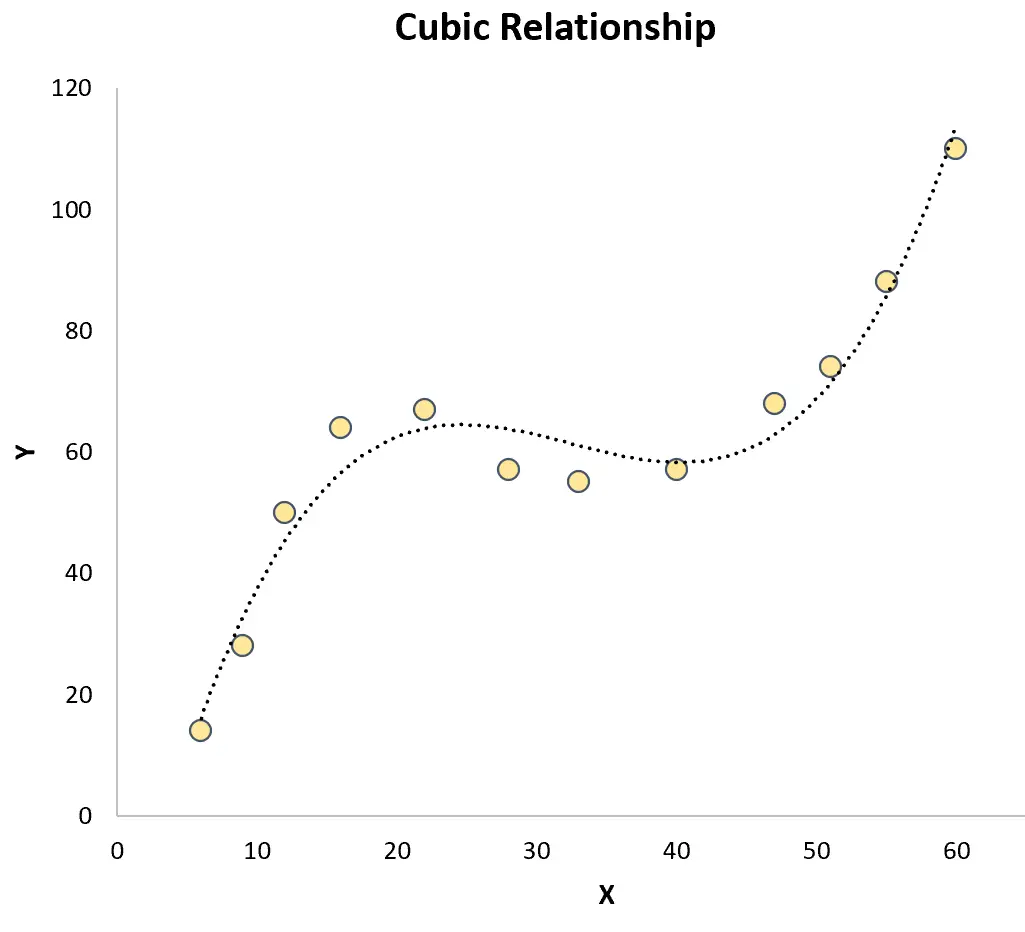
ये दोनों सरल रैखिक प्रतिगमन के विपरीत हैं जिसमें भविष्यवक्ता चर और प्रतिक्रिया चर के बीच संबंध रैखिक है:

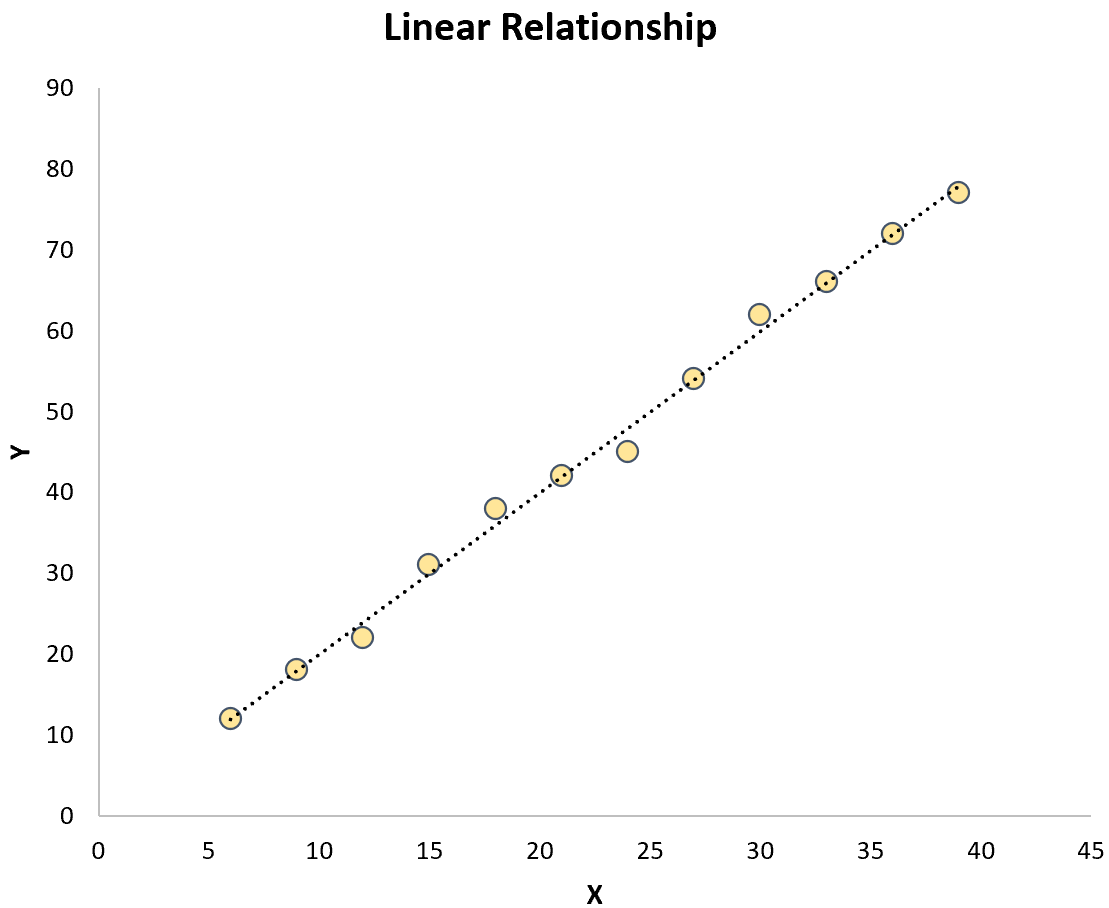
वक्ररेखीय प्रतिगमन मॉडल के लिए सूत्र

एक सरल रैखिक प्रतिगमन मॉडल निम्नलिखित सूत्र का उपयोग करके डेटा के एक सेट को फिट करने का प्रयास करता है:

ŷ = β ₀ + β ₁ एक्स

सोना:

• ŷ: प्रतिक्रिया चर
• β ₀ , β ₁ : प्रतिगमन गुणांक
• x: पूर्वानुमानित चर

इसके विपरीत, एक द्विघात प्रतिगमन मॉडल निम्नलिखित सूत्र का उपयोग करता है:

ŷ = β ₀ + β ₁ x + β ₂ x ²

और एक घन प्रतिगमन मॉडल निम्नलिखित सूत्र का उपयोग करता है:

ŷ = β ₀ + β ₁ x + β ₂ x ² + β ₃ x ³

प्रतिगमन मॉडल को दिया गया एक अधिक सामान्य नाम जिसमें घातांक शामिल हैं , बहुपद प्रतिगमन है, जो निम्नलिखित सूत्र लेता है:

ŷ = β ₀ + β ₁ x + β ₂ x ² + … + β _k x ^k

K का मान बहुपद की घात को दर्शाता है। हालाँकि डिग्री कोई भी सकारात्मक संख्या हो सकती है, व्यवहार में हम 3 या 4 से अधिक डिग्री वाले बहुपद प्रतिगमन मॉडल को शायद ही कभी फिट करते हैं।

प्रतिगमन मॉडल सूत्र में घातांक का उपयोग करके, बहुपद प्रतिगमन मॉडल सीधी रेखाओं के बजाय वक्रों को डेटा सेट में फिट करने में सक्षम होते हैं।

वक्रीय प्रतिगमन का उपयोग कब करें

यह जानने का सबसे आसान तरीका है कि आपको कर्विलीनियर रिग्रेशन का उपयोग करना चाहिए या नहीं, भविष्यवक्ता चर और प्रतिक्रिया चर का एक स्कैटरप्लॉट बनाना है।

यदि स्कैटरप्लॉट दो चर के बीच एक रैखिक संबंध दिखाता है, तो एक सरल रैखिक प्रतिगमन संभवतः उपयुक्त है।

हालाँकि, यदि स्कैटरप्लॉट भविष्यवक्ता और प्रतिक्रिया चर के बीच एक द्विघात, घन, या अन्य वक्रीय पैटर्न दिखाता है, तो वक्रीय प्रतिगमन संभवतः उपयोग करने के लिए अधिक उपयुक्त है।

आप एक साधारण रैखिक प्रतिगमन मॉडल और एक वक्ररेखीय प्रतिगमन मॉडल को भी फिट कर सकते हैं और यह निर्धारित करने के लिए प्रत्येक मॉडल के फिट किए गए आर-वर्ग मानों की तुलना कर सकते हैं कि कौन सा मॉडल डेटा के लिए सबसे अच्छा फिट प्रदान करता है।

समायोजित आर-वर्ग उपयोगी है क्योंकि यह आपको बताता है कि प्रतिक्रिया चर में कितना भिन्नता भविष्यवक्ता चर द्वारा समझाया जा सकता है, मॉडल में भविष्यवक्ता चर की संख्या के लिए समायोजित किया गया है।

सामान्य तौर पर, उच्चतम समायोजित आर-वर्ग मान वाला मॉडल डेटा सेट के लिए बेहतर फिट प्रदान करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर में बहुपद प्रतिगमन कैसे करें:

बहुपद प्रतिगमन का एक परिचय
एक्सेल में बहुपद प्रतिगमन कैसे करें
पायथन में बहुपद प्रतिगमन कैसे करें
आर में बहुपद प्रतिगमन कैसे करें