वर्णनात्मक या अनुमानात्मक आँकड़े: क्या अंतर है?

सांख्यिकी के क्षेत्र में दो मुख्य शाखाएँ हैं:

• वर्णनात्मक आँकड़े
• आनुमानिक आँकड़े

यह ट्यूटोरियल दोनों शाखाओं के बीच अंतर बताता है और प्रत्येक कुछ स्थितियों में उपयोगी क्यों है।

वर्णनात्मक आँकड़े

संक्षेप में, वर्णनात्मक आँकड़ों का उद्देश्य सारांश आँकड़ों, ग्राफ़ और तालिकाओं का उपयोग करके कच्चे डेटा के एक सेट का वर्णन करना है।

वर्णनात्मक आँकड़े उपयोगी होते हैं क्योंकि वे आपको कच्चे डेटा मानों की पंक्तियों और पंक्तियों को देखने की तुलना में डेटा के समूह को अधिक तेज़ी से और आसानी से समझने की अनुमति देते हैं।

उदाहरण के लिए, मान लें कि हमारे पास एक कच्चा डेटा सेट है जो किसी विशेष स्कूल में 1,000 छात्रों के परीक्षण स्कोर दिखा रहा है। हमें औसत परीक्षण स्कोर के साथ-साथ परीक्षण स्कोर के वितरण में भी रुचि हो सकती है।

वर्णनात्मक आँकड़ों का उपयोग करके, हम औसत स्कोर पा सकते हैं और एक ग्राफ़ बना सकते हैं जो हमें स्कोर के वितरण की कल्पना करने में मदद करता है।

यह हमें केवल कच्चे डेटा को देखने की तुलना में छात्र परीक्षण स्कोर को अधिक आसानी से समझने की अनुमति देता है।

वर्णनात्मक सांख्यिकी के सामान्य रूप

वर्णनात्मक सांख्यिकी के तीन सामान्य रूप हैं:

1. सारांश आँकड़े। ये वे आँकड़े हैं जो एक ही संख्या का उपयोग करके डेटा का सारांश प्रस्तुत करते हैं । सारांश सांख्यिकी के दो सामान्य प्रकार हैं:

• केंद्रीय प्रवृत्ति के माप : ये संख्याएँ बताती हैं कि डेटा सेट का केंद्र कहाँ है। उदाहरणों में औसत शामिल है   और मध्यिका .
• फैलाव माप: ये संख्याएँ डेटा सेट में मूल्यों के वितरण का वर्णन करती हैं। उदाहरणों में अंतराल , अंतरचतुर्थक सीमा , मानक विचलन और विचरण शामिल हैं।

2. ग्राफ़िक्स . चार्ट हमें डेटा को विज़ुअलाइज़ करने में मदद करते हैं। डेटा को विज़ुअलाइज़ करने के लिए उपयोग किए जाने वाले सामान्य प्रकार के चार्ट में बॉक्स प्लॉट , हिस्टोग्राम , स्टेम और लीफ प्लॉट और स्कैटर प्लॉट शामिल हैं।

3. टेबल्स . तालिकाएँ हमें यह समझने में मदद कर सकती हैं कि डेटा कैसे वितरित किया जाता है। तालिका का एक सामान्य प्रकार आवृत्ति तालिका है, जो हमें बताती है कि कितने डेटा मान निश्चित सीमाओं के भीतर आते हैं।

वर्णनात्मक आँकड़ों का उपयोग करने का उदाहरण

निम्नलिखित उदाहरण दर्शाता है कि हम वास्तविक दुनिया में वर्णनात्मक आँकड़ों का उपयोग कैसे कर सकते हैं।

मान लें कि एक निश्चित स्कूल में 1,000 छात्र सभी एक ही परीक्षा देते हैं। हम परीक्षण परिणामों के वितरण को समझना चाहते हैं, इसलिए हम निम्नलिखित वर्णनात्मक आंकड़ों का उपयोग करते हैं:

1. सारांश आँकड़े

औसत: 82.13 . यह हमें बताता है कि 1,000 छात्रों के बीच औसत परीक्षण स्कोर 82.13 है।

माध्यिका: 84. यह हमें बताता है कि सभी छात्रों में से आधे ने 84 से ऊपर अंक प्राप्त किए और दूसरे आधे ने 84 से नीचे अंक प्राप्त किए।

अधिकतम: 100. न्यूनतम: 45. यह हमें बताता है कि किसी भी छात्र द्वारा प्राप्त अधिकतम अंक 100 था और न्यूनतम अंक 45 था। सीमा – जो हमें अधिकतम और न्यूनतम के बीच का अंतर बताती है – 55 है।

2. ग्राफ़िक्स

परीक्षण परिणामों के वितरण की कल्पना करने के लिए, हम एक हिस्टोग्राम बना सकते हैं – एक प्रकार का चार्ट जो आवृत्तियों को दर्शाने के लिए आयताकार पट्टियों का उपयोग करता है।

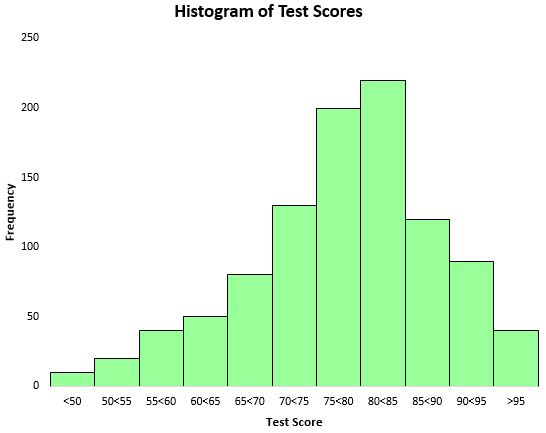
इस हिस्टोग्राम के आधार पर, हम देख सकते हैं कि परीक्षण अंकों का वितरण मोटे तौर पर घंटी के आकार का है। अधिकांश छात्रों ने 70 और 90 के बीच अंक प्राप्त किए, जबकि बहुत कम छात्रों ने 95 से अधिक अंक प्राप्त किए और बहुत कम छात्रों ने 50 से नीचे अंक प्राप्त किए।

3. टेबल्स

अंकों के वितरण को समझने का एक और आसान तरीका एक आवृत्ति तालिका बनाना है। उदाहरण के लिए, निम्नलिखित आवृत्ति तालिका विभिन्न श्रेणियों के बीच स्कोर करने वाले छात्रों का प्रतिशत दर्शाती है:

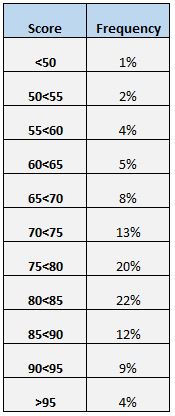
हम देख सकते हैं कि कुल छात्रों में से केवल 4% ने 95 से अधिक अंक प्राप्त किए। हम यह भी देख सकते हैं कि (12% + 9% + 4% = ) सभी छात्रों में से 25% ने 85 या उससे अधिक अंक प्राप्त किए।

एक आवृत्ति तालिका विशेष रूप से उपयोगी होती है यदि हम यह जानना चाहते हैं कि कितने प्रतिशत डेटा मान एक निश्चित मूल्य से ऊपर या नीचे हैं। उदाहरण के लिए, मान लीजिए कि स्कूल 75 से ऊपर के किसी भी स्कोर को “स्वीकार्य” टेस्ट स्कोर मानता है।

आवृत्ति तालिका को देखते हुए, हम आसानी से देख सकते हैं कि (20% + 22% + 12% + 9% + 4% = ) 67% छात्रों ने परीक्षण में स्वीकार्य अंक प्राप्त किया।

आनुमानिक आँकड़े

संक्षेप में, अनुमानित आँकड़े उस बड़ी आबादी के बारे में निष्कर्ष निकालने के लिए डेटा के एक छोटे नमूने का उपयोग करते हैं जहाँ से नमूना लिया जाता है।

उदाहरण के लिए, हम किसी देश के लाखों लोगों की राजनीतिक प्राथमिकताओं को समझना चाह सकते हैं।

हालाँकि, देश में प्रत्येक व्यक्ति का सर्वेक्षण करना बहुत समय लेने वाला और महंगा होगा। इसलिए, इसके बजाय हम 1,000 अमेरिकियों का एक छोटा सर्वेक्षण करेंगे, और समग्र रूप से जनसंख्या के बारे में निष्कर्ष निकालने के लिए सर्वेक्षण परिणामों का उपयोग करेंगे।

यह अनुमानित आँकड़ों का संपूर्ण आधार है: हम किसी जनसंख्या के बारे में एक प्रश्न का उत्तर देना चाहते हैं, इसलिए हम उस जनसंख्या के एक छोटे नमूने के लिए डेटा प्राप्त करते हैं और जनसंख्या के बारे में निष्कर्ष निकालने के लिए नमूना डेटा का उपयोग करते हैं।

प्रतिनिधि नमूने का महत्व

किसी जनसंख्या के बारे में निष्कर्ष निकालने के लिए एक नमूने का उपयोग करने की हमारी क्षमता में आश्वस्त होने के लिए, हमें यह सुनिश्चित करना चाहिए कि हमारे पास एक प्रतिनिधि नमूना है, अर्थात, एक ऐसा नमूना जिसमें जनसंख्या में व्यक्तियों की विशेषताएं नमूना से बारीकी से मेल खाती हैं। विशेषताएँ। कुल जनसंख्या का.

आदर्श रूप से, हम चाहते हैं कि हमारा नमूना हमारी जनसंख्या के “लघु संस्करण” जैसा दिखे। इस प्रकार, यदि हम 50% लड़कियों और 50% लड़कों से बनी छात्रों की आबादी के बारे में निष्कर्ष निकालना चाहते हैं, तो हमारा नमूना प्रतिनिधि नहीं होगा यदि इसमें 90% लड़के और केवल 10% लड़कियां शामिल हों।

यदि हमारा नमूना समग्र जनसंख्या के समान नहीं है, तो हम आत्मविश्वास से नमूने से समग्र जनसंख्या के परिणामों को सामान्यीकृत नहीं कर सकते।

प्रतिनिधि नमूना कैसे प्राप्त करें

प्रतिनिधि नमूना प्राप्त करने की संभावना को अधिकतम करने के लिए, आपको दो बातों पर ध्यान देना चाहिए:

1. सुनिश्चित करें कि आप यादृच्छिक नमूनाकरण विधि का उपयोग करें।

ऐसी कई यादृच्छिक नमूनाकरण विधियाँ हैं जिनका उपयोग आप कर सकते हैं जिनसे एक प्रतिनिधि नमूना तैयार होने की संभावना है, जिनमें शामिल हैं:

• एक साधारण यादृच्छिक नमूना
• एक व्यवस्थित यादृच्छिक नमूना
• एक क्लस्टर यादृच्छिक नमूना
• एक स्तरीकृत यादृच्छिक नमूना

यादृच्छिक नमूनाकरण विधियाँ प्रतिनिधि नमूने उत्पन्न करती हैं क्योंकि जनसंख्या के प्रत्येक सदस्य के पास नमूने में शामिल होने की समान संभावना होती है।

2. सुनिश्चित करें कि आपका नमूना आकार काफी बड़ा है ।

उपयुक्त नमूनाकरण पद्धति का उपयोग करने के अलावा, यह सुनिश्चित करना महत्वपूर्ण है कि नमूना इतना बड़ा हो कि आपके पास बड़ी आबादी के लिए सामान्यीकरण करने में सक्षम होने के लिए पर्याप्त डेटा हो।

अपना नमूना आकार निर्धारित करने के लिए, आपको उस जनसंख्या के आकार पर विचार करना होगा जिसका आप अध्ययन कर रहे हैं, जिस आत्मविश्वास का स्तर आप उपयोग करना चाहते हैं, और त्रुटि का मार्जिन जिसे आप स्वीकार्य मानते हैं।

सौभाग्य से, आप इन मानों को दर्ज करने के लिए ऑनलाइन कैलकुलेटर का उपयोग कर सकते हैं और देख सकते हैं कि आपका नमूना आकार क्या होना चाहिए।

अनुमानात्मक आँकड़ों के सामान्य रूप

अनुमानात्मक आँकड़ों के तीन सामान्य रूप हैं:

1. परिकल्पना परीक्षण.

हम अक्सर जनसंख्या के बारे में प्रश्नों का उत्तर देना चाहते हैं जैसे:

• क्या ओहायो में उम्मीदवार ए का समर्थन करने वाले लोगों का प्रतिशत 50% से अधिक है?
• क्या किसी पौधे की औसत ऊंचाई 14 इंच के बराबर होती है?
• क्या स्कूल A और स्कूल B में छात्रों की औसत ऊंचाई के बीच अंतर है?

इन सवालों का जवाब देने के लिए, हम परिकल्पना परीक्षण कर सकते हैं, जो हमें आबादी के बारे में निष्कर्ष निकालने के लिए नमूने से डेटा का उपयोग करने की अनुमति देता है।

2. आत्मविश्वास अंतराल .

कभी-कभी हम किसी जनसंख्या के लिए एक निश्चित मूल्य का अनुमान लगाना चाहते हैं। उदाहरण के लिए, हमें ऑस्ट्रेलिया में एक निश्चित पौधों की प्रजाति की औसत ऊंचाई में रुचि हो सकती है।

देश में चारों ओर घूमने और प्रत्येक पौधे को मापने के बजाय, हम पौधों का एक छोटा सा नमूना एकत्र कर सकते हैं और प्रत्येक को माप सकते हैं। फिर हम जनसंख्या की औसत ऊंचाई का अनुमान लगाने के लिए नमूने में पौधों की औसत ऊंचाई का उपयोग कर सकते हैं।

हालाँकि, हमारा नमूना पूर्ण जनसंख्या अनुमान प्रदान करने की संभावना नहीं है। सौभाग्य से, हम एक विश्वास अंतराल बनाकर इस अनिश्चितता का हिसाब लगा सकते हैं, जो मूल्यों की एक श्रृंखला प्रदान करता है जिसके भीतर हमें विश्वास है कि वास्तविक जनसंख्या पैरामीटर निहित है।

उदाहरण के लिए, हम [13.2, 14.8] का 95% विश्वास अंतराल उत्पन्न कर सकते हैं, जिसका अर्थ है कि हम 95% आश्वस्त हैं कि इस पौधे की प्रजाति की वास्तविक औसत ऊंचाई 13.2 इंच और 14.8 इंच के बीच है।

3. प्रतिगमन .

कभी-कभी हम किसी जनसंख्या में दो चरों के बीच संबंध को समझना चाहते हैं।

उदाहरण के लिए, मान लें कि हम जानना चाहते हैं कि प्रति सप्ताह अध्ययन में बिताए गए घंटे परीक्षण स्कोर से संबंधित हैं या नहीं। इस प्रश्न का उत्तर देने के लिए, हम प्रतिगमन विश्लेषण नामक एक तकनीक का प्रयोग कर सकते हैं।

इसलिए, हम 100 छात्रों के लिए अध्ययन किए गए घंटों की संख्या के साथ-साथ परीक्षण स्कोर को भी देख सकते हैं और यह देखने के लिए एक प्रतिगमन विश्लेषण कर सकते हैं कि क्या दोनों चर के बीच कोई महत्वपूर्ण संबंध है।

यदि प्रतिगमन का पी-मूल्य महत्वपूर्ण पाया जाता है , तो हम यह निष्कर्ष निकाल सकते हैं कि समग्र छात्र आबादी में इन दो चर के बीच एक महत्वपूर्ण संबंध है।

वर्णनात्मक और अनुमानात्मक आँकड़ों के बीच अंतर

संक्षेप में, वर्णनात्मक और अनुमानात्मक आँकड़ों के बीच अंतर को इस प्रकार वर्णित किया जा सकता है:

वर्णनात्मक आँकड़े डेटा के एक सेट का वर्णन करने के लिए सारांश आँकड़ों, ग्राफ़ और तालिकाओं का उपयोग करते हैं।

यह सभी व्यक्तिगत डेटा मानों पर गौर किए बिना डेटा के एक सेट को जल्दी और आसानी से समझने में हमारी मदद करने के लिए उपयोगी है।

अनुमानित आँकड़े बड़ी आबादी के बारे में निष्कर्ष निकालने के लिए नमूनों का उपयोग करते हैं।

आप किसी जनसंख्या के बारे में जिस प्रश्न का उत्तर देना चाहते हैं, उसके आधार पर आप निम्नलिखित विधियों में से एक या अधिक का उपयोग करने का निर्णय ले सकते हैं: परिकल्पना परीक्षण, आत्मविश्वास अंतराल और प्रतिगमन विश्लेषण।

यदि आप इनमें से किसी एक विधि का उपयोग करना चुनते हैं, तो ध्यान रखें कि आपका नमूना आपकी जनसंख्या का प्रतिनिधि होना चाहिए , अन्यथा आपके द्वारा निकाले गए निष्कर्ष विश्वसनीय नहीं होंगे।