सांख्यिकी में मोड क्यों महत्वपूर्ण है?

मोड उस मान का प्रतिनिधित्व करता है जो डेटा सेट में सबसे अधिक बार दिखाई देता है।

एक डेटा सेट में कोई मोड नहीं हो सकता है (यदि कोई मान दोहराता नहीं है), एक मोड, या एकाधिक मोड।

उदाहरण के लिए, निम्नलिखित डेटासेट में मोड 19 है:

डेटासेट: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

यह वह मान है जो सबसे अधिक बार प्रकट होता है.

सांख्यिकी में, मोड निम्नलिखित कारणों से महत्वपूर्ण है:

कारण 1 : इससे हमें पता चलता है कि डेटा सेट में कौन से मान सबसे आम हैं।

कारण 2 : जब माध्य और माध्यिका की गणना नहीं की जा सकती, तो यह श्रेणीबद्ध डेटा में सबसे लगातार मान खोजने के लिए उपयोगी है।

कारण 3 : यह हमें एक अंदाज़ा देता है कि डेटा सेट का “केंद्र” कहाँ है, भले ही माध्यिका और माध्य का अधिक सामान्यतः उपयोग किया जाता है (जैसा कि हम इस लेख में बाद में देखेंगे)।

निम्नलिखित उदाहरण व्यवहार में इनमें से प्रत्येक कारण को दर्शाते हैं।

कारण 1: मोड हमें बताता है कि कौन सा मान सबसे सामान्य है

मान लीजिए कि हमारे पास 100,000 पंक्तियों का एक डेटासेट है जिसमें संयुक्त राज्य अमेरिका में घरों की बिक्री कीमतें शामिल हैं:

मान लीजिए कि हम इस डेटासेट के मोड की गणना करने के लिए सांख्यिकीय सॉफ़्टवेयर (जैसे एक्सेल , आर , पायथन , आदि) का उपयोग करते हैं और पाते हैं कि तीन मोड हैं:

• $280,000
• $300,000
• $305,000

इससे हमें तुरंत डेटासेट में सबसे आम घर की कीमतों का अंदाजा हो जाता है।

मोड हज़ारों की गणना करना डेटा की पंक्तियों को देखने और यह पहचानने की कोशिश करने से भी अधिक तेज़ है कि किस घर की कीमतें सबसे अधिक बार होती हैं।

कारण 2: मोड श्रेणीबद्ध डेटा में सबसे सामान्य मान की खोज करता है

मान लीजिए कि हमारे पास 1,000 पंक्तियों का एक डेटासेट है जो हमें एक निश्चित पड़ोस में व्यक्तियों के स्वामित्व वाली कार का रंग बताता है:

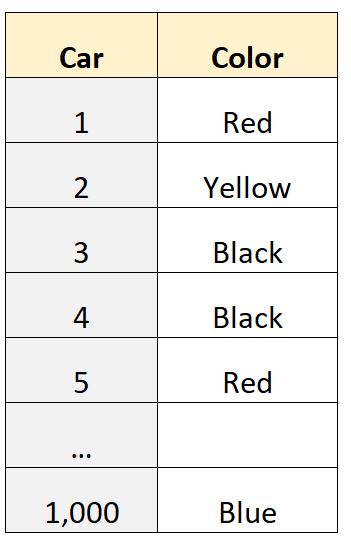
परिवर्तनीय “रंग” एक श्रेणीगत चर है, जिसका अर्थ है कि मान श्रेणियों (“लाल”, “पीला”, “काला”, आदि) से संबंधित हैं और इसलिए हम औसत या माध्य जैसे मात्रात्मक मान की गणना नहीं कर सकते हैं .

हालाँकि, हम मोड की गणना कर सकते हैं क्योंकि यह केवल डेटा सेट में सबसे सामान्य मान का प्रतिनिधित्व करता है।

उदाहरण के लिए, हम यह निर्धारित करने के लिए सांख्यिकीय सॉफ़्टवेयर का उपयोग कर सकते हैं कि इस डेटासेट का मोड “काला” है, जो हमें बताता है कि इस डेटासेट में सबसे आम कार का रंग काला है।

कारण 3: मोड हमें यह अंदाज़ा देता है कि डेटा सेट का केंद्र कहाँ है

मोड को केंद्रीय प्रवृत्ति का माप भी माना जाता है, जिसका अर्थ है कि यह हमें यह अंदाजा दे सकता है कि डेटा सेट का “केंद्र” कहां है।

उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित डेटासेट है जो एक कक्षा में 20 विभिन्न छात्रों के परीक्षा स्कोर दिखाता है:

मोड 82 निकला – यह सबसे सामान्य परीक्षा स्कोर है। यह इस बात का भी एक अच्छा संकेत है कि इस डेटासेट में “मुख्य” समीक्षा स्कोर मान कहाँ निहित है।

हालाँकि, मान लीजिए कि इसके बजाय हमारे पास परीक्षा परिणामों के निम्नलिखित डेटासेट हैं:

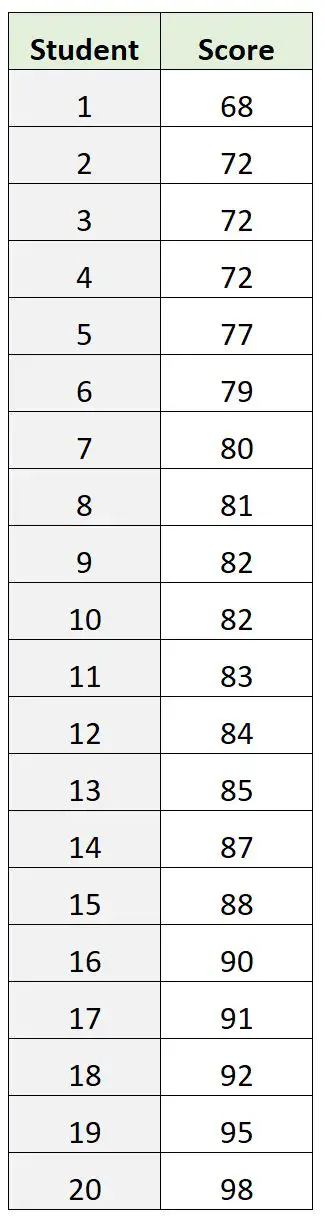
इस डेटासेट में, 72 फैशन परीक्षा स्कोर है। हालाँकि, यह इस बात का ख़राब संकेत है कि परीक्षा का “मुख्य” स्कोर कहाँ है।

औसत परीक्षा स्कोर 82.9 है और औसत परीक्षा स्कोर 82.5 है, ये दोनों हमें एक बेहतर विचार देते हैं कि फैशन के संबंध में “केंद्रीय” मूल्य कहां है।

सारांश

इस आलेख में शामिल मुख्य बिंदुओं का संक्षिप्त सारांश यहां दिया गया है:

• मोड उन मानों का प्रतिनिधित्व करता है जो डेटा सेट में सबसे अधिक बार दिखाई देते हैं।
• जब माध्य और माध्यिका का उपयोग नहीं किया जा सकता है तो मोड हमें श्रेणीबद्ध डेटा में सबसे सामान्य मान बताता है।
• मोड हमें यह अंदाज़ा देता है कि डेटा सेट का “केंद्र” कहाँ है, लेकिन माध्य या माध्यिका से तुलना करने पर यह भ्रामक हो सकता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सांख्यिकी में माध्य, माध्यिका और मोड के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सांख्यिकी में औसत क्यों महत्वपूर्ण है?
सांख्यिकी में माध्यिका क्यों महत्वपूर्ण है?
ठोस उदाहरण: माध्य, माध्यिका और बहुलक का उपयोग करना
माध्य बनाम का उपयोग कब करें माध्यिका: उदाहरण सहित