सांख्यिकी में विषमता की व्याख्या कैसे करें: उदाहरणों के साथ

आंकड़ों में, हम वितरण की समरूपता का वर्णन करने के लिए तिरछापन का उपयोग करते हैं।

हम कहते हैं कि डेटा मानों का वितरण विषम है यदि वितरण के बाईं ओर “पूंछ” है:

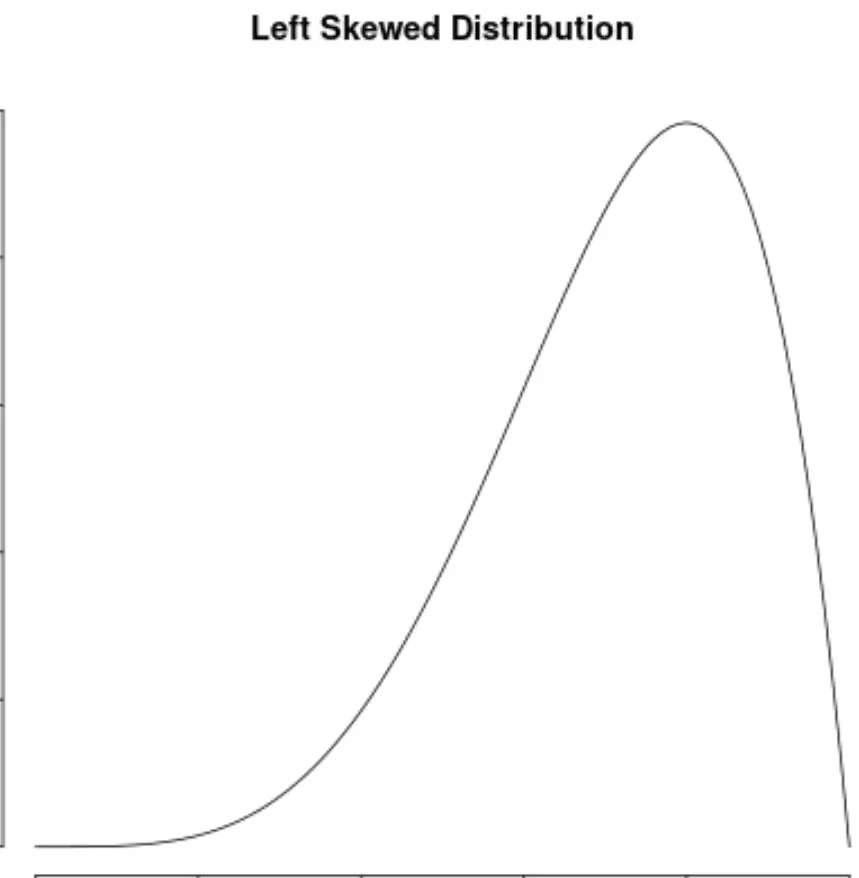
एक वितरण को दाहिना तिरछा तब कहा जाता है जब वितरण के दाहिनी ओर “पूंछ” हो:

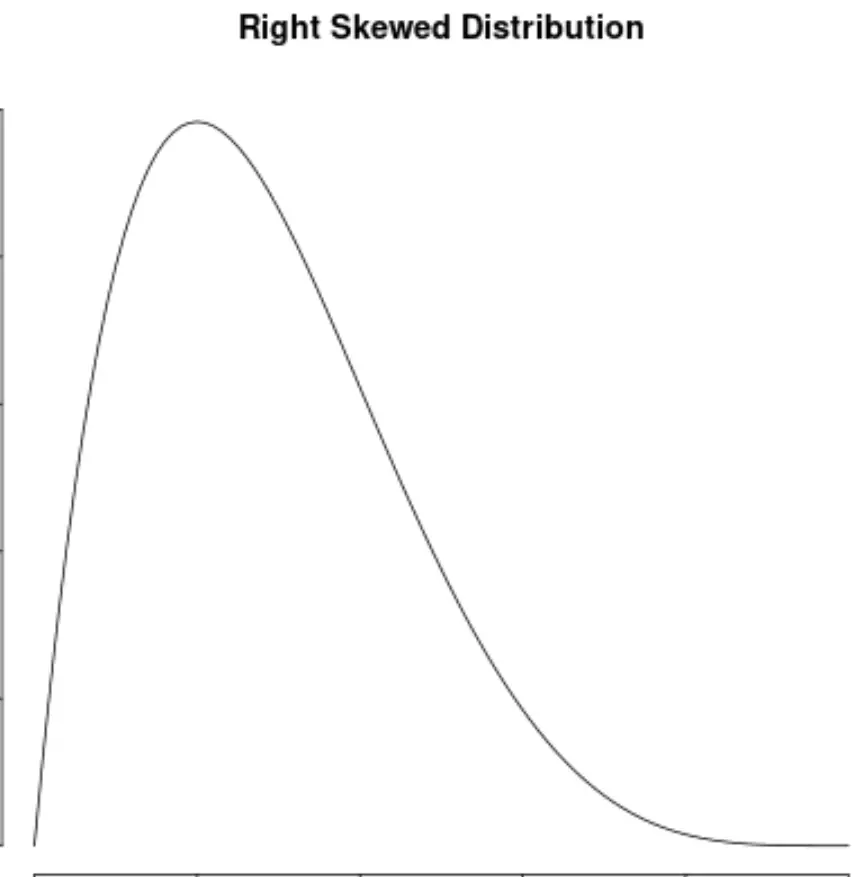
और हम कहते हैं कि किसी वितरण में कोई विषमता नहीं है यदि वह दोनों तरफ सममित है:

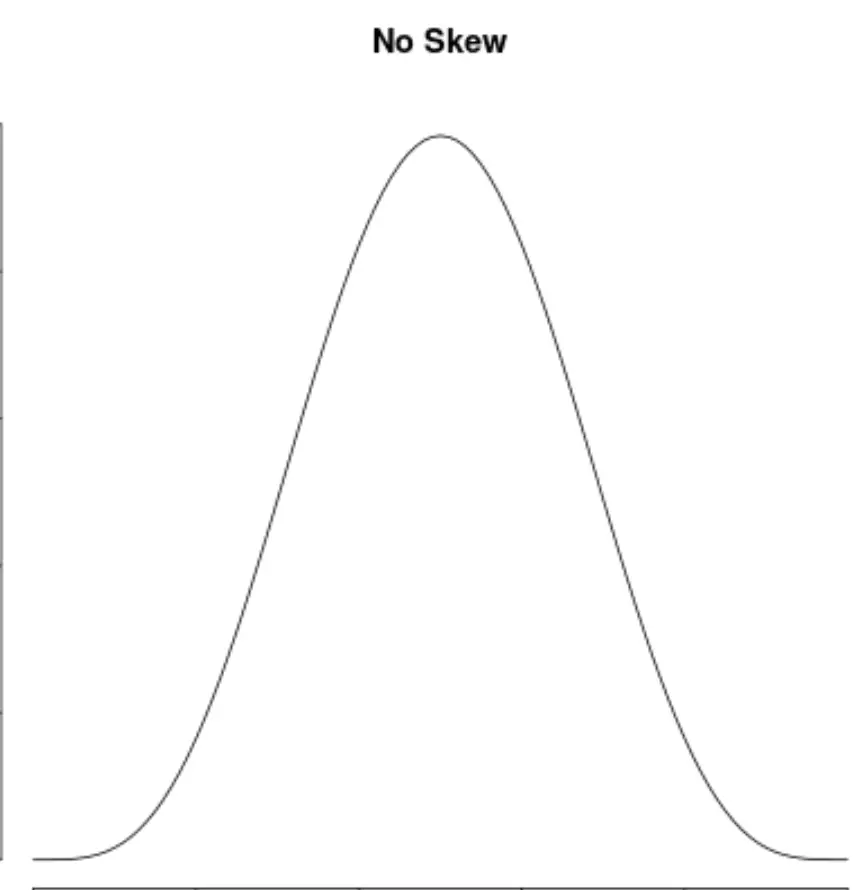
विषमता की व्याख्या कैसे करें

विषमता का मान ऋणात्मक अनंत से लेकर सकारात्मक अनंत तक हो सकता है।

यहां विषमता मूल्यों की व्याख्या करने का तरीका बताया गया है:

• तिरछापन के लिए एक नकारात्मक मान इंगित करता है कि पूंछ वितरण के बाईं ओर है, जो अधिक नकारात्मक मूल्यों की ओर बढ़ती है।
• तिरछापन के लिए एक सकारात्मक मूल्य इंगित करता है कि पूंछ वितरण के दाईं ओर है, जो अधिक सकारात्मक मूल्यों की ओर बढ़ती है।
• शून्य का मान इंगित करता है कि वितरण में कोई विषमता नहीं है, जिसका अर्थ है कि वितरण पूरी तरह से सममित है।

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में विषमता मूल्यों की व्याख्या कैसे करें।

उदाहरण 1: बाएँ-तिरछा वितरण

अधिकांश आबादी में मृत्यु का आयु वितरण बाईं ओर झुका हुआ है। अधिकांश लोग 70 से 80 वर्ष की आयु के बीच रहते हैं, और इस आयु से कम ही लोग जीवित रहते हैं।

यदि हमने मृत्यु की आयु के मूल्यों के वितरण की कल्पना करने के लिए एक घनत्व प्लॉट बनाया, तो यह इस तरह दिख सकता है:

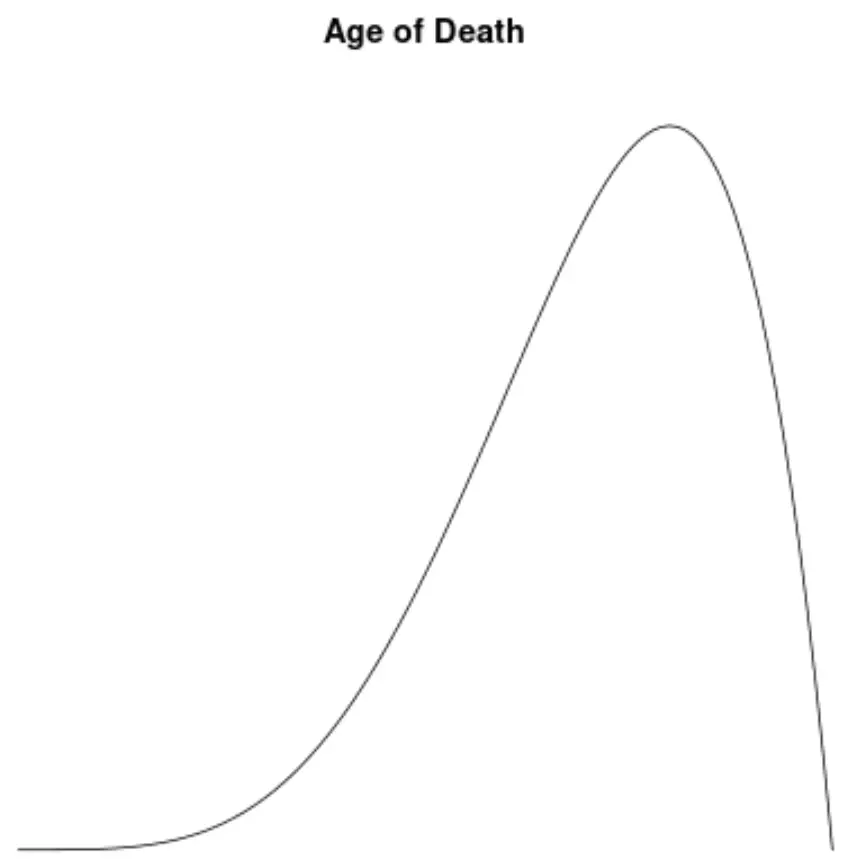
मान लीजिए हम इस वितरण की विषमता की गणना करते हैं और पाते हैं कि यह -1.3225 है।

चूँकि यह मान ऋणात्मक है, इसलिए हम इसकी व्याख्या इस अर्थ में करते हैं कि वितरण बाएँ-तिरछा है, जिसका अर्थ है कि पूंछ वितरण के बाईं ओर फैली हुई है।

उदाहरण 2: दाएँ-तिरछा वितरण

संयुक्त राज्य अमेरिका में घरेलू आय का वितरण दाहिनी ओर झुका हुआ है, अधिकांश परिवार प्रति वर्ष $30,000 और $70,000 के बीच कमाते हैं, लेकिन परिवारों की दाहिनी ओर लंबी आय कहीं अधिक है।

यदि हम घरेलू आय मूल्यों के वितरण की कल्पना करने के लिए एक घनत्व प्लॉट बनाते हैं, तो यह इस तरह दिख सकता है:

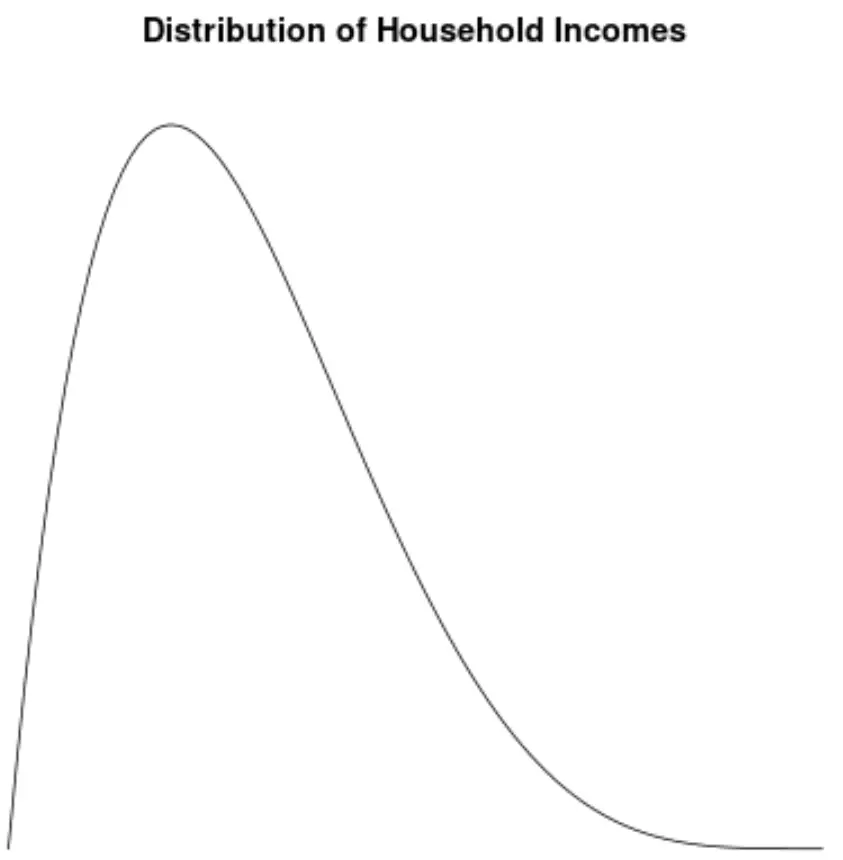
मान लीजिए हम इस वितरण की विषमता की गणना करते हैं और पाते हैं कि यह 2.0043 है।

चूँकि यह मान सकारात्मक है, हम इसकी व्याख्या इस अर्थ में करते हैं कि वितरण दाईं ओर तिरछा है, जिसका अर्थ है कि पूंछ वितरण के दाईं ओर फैली हुई है।

उदाहरण 3: कोई पूर्वाग्रह नहीं

नर का आकार लगभग सामान्य रूप से वितरित होता है और कोई विषमता नहीं दिखाता है। उदाहरण के लिए, संयुक्त राज्य अमेरिका में एक आदमी की औसत ऊंचाई लगभग 69.1 इंच है। ऊंचाई का वितरण लगभग सममित है, कुछ छोटे और कुछ लम्बे हैं।

यदि हमने संयुक्त राज्य अमेरिका में पुरुष ऊंचाई के वितरण की कल्पना करने के लिए एक घनत्व चार्ट बनाया, तो यह इस तरह दिख सकता है:

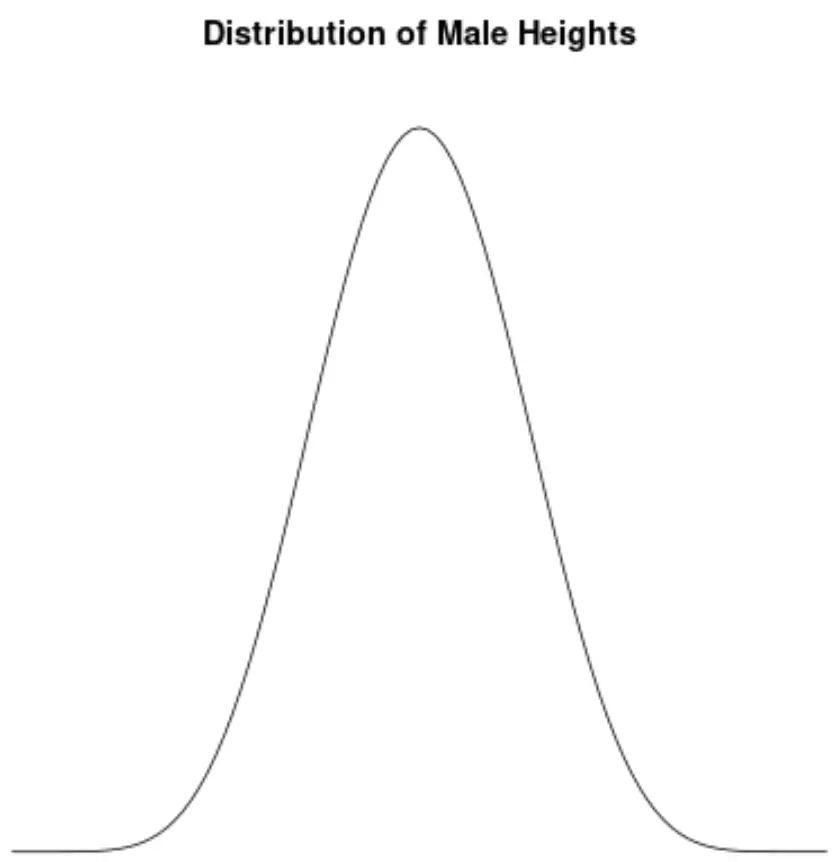
मान लीजिए हम इस वितरण की विषमता की गणना करते हैं और पाते हैं कि यह 0.0013 है।

चूँकि यह मान शून्य के करीब है, हम इसकी व्याख्या इस तरह करते हैं कि वितरण में वस्तुतः कोई तिरछापन नहीं है, जिसका अर्थ है कि वितरण के दोनों ओर के अंत लगभग बराबर हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल विषम आँकड़ों के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सकारात्मक रूप से विषम वितरण के 5 उदाहरण
नकारात्मक रूप से विषम वितरण के 5 उदाहरण
एक्सेल में तिरछापन की गणना कैसे करें
बॉक्स प्लॉट्स में विषमता की पहचान कैसे करें