विषमता के प्रकार

इस लेख में आप जानेंगे कि सांख्यिकी में कितने प्रकार की विषमताएँ मौजूद हैं। इस प्रकार, प्रत्येक प्रकार की विषमता को उदाहरणों के साथ समझाया गया है और इसके अलावा, आप यह देख पाएंगे कि वितरण की विषमता की गणना कैसे की जाती है।

विषमता के प्रकार क्या हैं?

सांख्यिकी में, विषमता तीन प्रकार की होती है:

• सकारात्मक विषमता : वितरण में बाईं ओर की तुलना में माध्य के दाईं ओर अधिक भिन्न मान होते हैं।
• नकारात्मक तिरछापन : वितरण में माध्य के दाईं ओर की तुलना में बाईं ओर अधिक भिन्न मान होते हैं।
• समरूपता : वितरण में माध्य के बाएँ और दाएँ मानों की संख्या समान होती है।

प्रत्येक प्रकार की विषमता को नीचे अधिक विस्तार से समझाया गया है।

सकारात्मक विषमता

जब किसी वितरण में सकारात्मक तिरछापन होता है, तो इसका मतलब है कि उसके ग्राफ में दाहिनी पूंछ बाईं पूंछ से अधिक लंबी है। अर्थात्, वितरण में माध्य के दाईं ओर अधिक भिन्न मान होते हैं।

पिछले उदाहरण में वक्र सकारात्मक रूप से असममित है क्योंकि माध्य के दाईं ओर बाईं ओर की तुलना में कई अधिक मान हैं। जैसा कि आप चार्ट से देख सकते हैं, हरे रंग में दिखाई गई पट्टी नारंगी पट्टी से बहुत बड़ी है।

नकारात्मक विषमता

आँकड़ों में, किसी वितरण को ऋणात्मक विषमता तब कहा जाता है जब उसके ग्राफ में बायाँ पूँछ दाएँ पूँछ से अधिक लंबा होता है। अर्थात्, एक नकारात्मक रूप से विषम वितरण का अर्थ है कि इसमें माध्य के बाईं ओर अधिक भिन्न मान हैं।

यदि आप पिछले ग्राफ़ को देखें, तो माध्य के बाईं ओर दाईं ओर की तुलना में अधिक मान हैं, इसलिए वक्र नकारात्मक रूप से तिरछा है।

समरूपता

एक वितरण सममित होता है जब माध्य के बाईं ओर के मानों की संख्या माध्य के दाईं ओर के मानों की संख्या के बराबर होती है। इसलिए औसत समरूपता की धुरी के रूप में कार्य करता है।

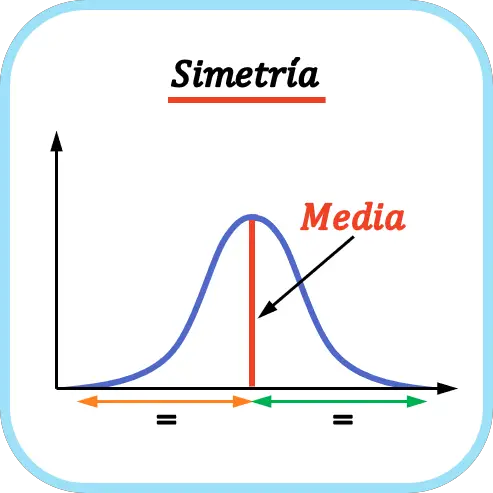
जैसा कि ऊपर दिए गए उदाहरण में दिखाया गया है, प्रस्तुत संभाव्यता वितरण के माध्य के बाईं ओर के मानों की संख्या माध्य के दाईं ओर के मानों की संख्या से मेल खाती है, इसलिए यह एक सममित वितरण है।

विषमता के प्रकार का निर्धारण कैसे करें

अब जब हम जानते हैं कि आंकड़ों में विषमता के विभिन्न प्रकार क्या हैं, तो आइए देखें कि यह कैसे जाना जाए कि संभाव्यता वितरण किस प्रकार की विषमता से मेल खाता है।

परंपरागत रूप से, यह समझाया जाता है कि हम किसी वितरण की विषमता के प्रकार को उसके माध्य और माध्यिका (चाहे वह बड़ा, समतुल्य या छोटा हो) के बीच संबंध के आधार पर जान सकते हैं। हालाँकि, यह संपत्ति हमेशा संतुष्ट नहीं होती है। इस प्रकार, किसी वितरण की विषमता निर्धारित करने के लिए, फिशर की विषमता गुणांक की गणना की जानी चाहिए।

फिशर असममिति गुणांक की गणना निम्न सूत्र का उपयोग करके की जाती है:

या उसके बराबर:

सोना

गणितीय अपेक्षा है,

अंकगणित माध्य और

मानक विचलन .

और एक बार फिशर गुणांक की गणना हो जाने के बाद, इसका संकेत यह निर्धारित करना संभव बनाता है कि वितरण किस प्रकार की विषमता प्रस्तुत करता है:

• यदि फिशर का विषमता गुणांक सकारात्मक है, तो वितरण सकारात्मक रूप से विषम है।
• यदि फिशर का विषमता गुणांक ऋणात्मक है, तो वितरण ऋणात्मक रूप से विषम है।
• यदि वितरण सममित है, तो फिशर का तिरछापन गुणांक शून्य के बराबर है (विपरीत हमेशा सत्य नहीं होता है)।