वेइबुल वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि वेइबुल वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसके अतिरिक्त, आप वेइबुल वितरण का ग्राफिकल प्रतिनिधित्व देख पाएंगे और इस प्रकार की संभाव्यता वितरण के गुण क्या हैं।

वेइबुल वितरण क्या है?

वेइबुल वितरण एक सतत संभाव्यता वितरण है जो दो विशिष्ट मापदंडों द्वारा परिभाषित है: आकार पैरामीटर α और स्केल पैरामीटर λ।

आंकड़ों में, वेइबुल वितरण का उपयोग मुख्य रूप से उत्तरजीविता विश्लेषण के लिए किया जाता है। इसी तरह, वेइबुल वितरण के विभिन्न क्षेत्रों में कई अनुप्रयोग हैं। हम नीचे वेइबुल वितरण का उपयोग करने के बारे में विस्तार से जानेंगे।

$X\sim\text{Weibull}(\alpha,\lambda)$

लेखकों के अनुसार, वेइबुल वितरण को तीन मापदंडों के साथ भी मानकीकृत किया जा सकता है। फिर, थ्रेशोल्ड वैल्यू नामक एक तीसरा पैरामीटर जोड़ा जाता है, जो एब्सिस्सा को इंगित करता है जिस पर वितरण ग्राफ शुरू होता है।

वेइबुल वितरण का नाम स्वेड वालोडी वेइबुल के नाम पर रखा गया है, जिन्होंने 1951 में इसका विस्तार से वर्णन किया था। हालांकि, वेइबुल वितरण की खोज 1927 में मौरिस फ्रैचेट द्वारा की गई थी और पहली बार 1933 में रोसिन और रैमलर द्वारा लागू किया गया था।

वेइबुल वितरण को प्लॉट करना

एक बार जब हमने वेइबुल वितरण की परिभाषा देख ली, तो हम देखेंगे कि इसके मापदंडों के मूल्यों के आधार पर इसका ग्राफिकल प्रतिनिधित्व कैसे भिन्न होता है।

नीचे आप कई उदाहरण देख सकते हैं कि वेइबुल वितरण का घनत्व फ़ंक्शन ग्राफ़ आकार पैरामीटर और स्केल पैरामीटर के मान के आधार पर कैसे भिन्न होता है।

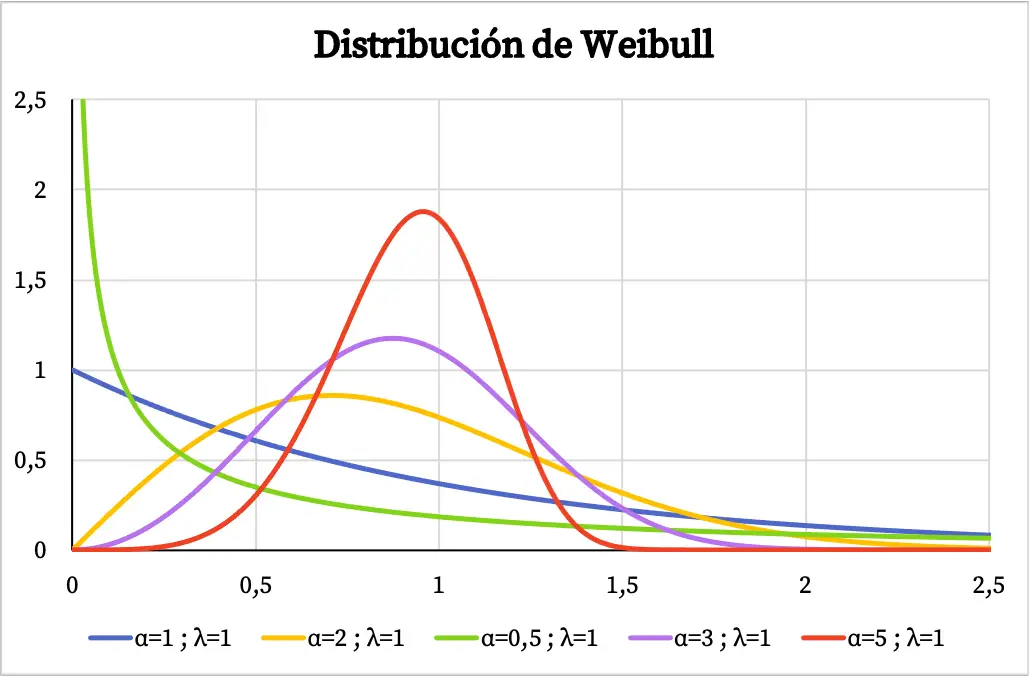
जब वेइबुल वितरण का उपयोग समय के एक फ़ंक्शन के रूप में किसी सिस्टम की विफलता दर को मॉडल करने के लिए किया जाता है, तो आकार पैरामीटर α का मान निम्नलिखित का मतलब है:

α<1: समय के साथ विफलता दर कम हो जाती है।
α=1: विफलता दर समय के साथ स्थिर रहती है।
α>1: समय के साथ विफलता दर बढ़ती है।

दूसरी ओर, निम्नलिखित ग्राफ़ में आप इसके विशिष्ट मूल्यों के आधार पर प्लॉट किए गए वेइबुल वितरण के संचयी संभाव्यता फ़ंक्शन को देख सकते हैं।

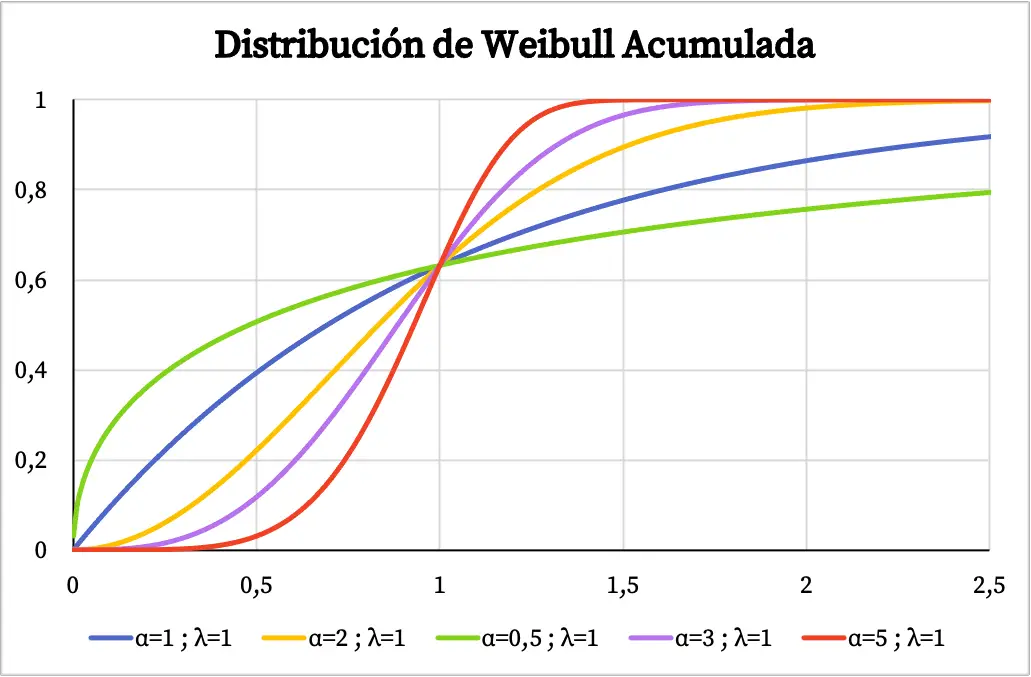
वेइबुल वितरण की विशेषताएँ

वेइबुल वितरण में निम्नलिखित विशेषताएं हैं:

वेइबुल वितरण में दो विशिष्ट पैरामीटर हैं जो इसके ग्राफ को परिभाषित करते हैं: आकार पैरामीटर α और स्केल पैरामीटर λ। दोनों पैरामीटर सकारात्मक वास्तविक संख्याएँ हैं।

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul> <li> वेइबुल वितरण केवल सकारात्मक एब्सिस्सा मान स्वीकार करता है।</li> </ul> <p class=$ $x\in (0,+\infty)$

वेइबुल वितरण के माध्य की गणना निम्नलिखित सूत्र से की जाती है:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

दूसरी ओर, वेइबुल वितरण का विचरण ज्ञात करने का सूत्र है:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

एक यादृच्छिक चर का मोड जो α>1 के साथ वेइबुल वितरण का अनुसरण करता है, निम्नलिखित अभिव्यक्ति द्वारा निर्धारित किया जा सकता है:

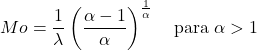
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul> <li> वेइबुल वितरण के घनत्व फलन का सूत्र है:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

इसी प्रकार, वेइबुल वितरण के संचयी संभाव्यता फ़ंक्शन का सूत्र है:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

वेइबुल वितरण के विषमता गुणांक की गणना निम्नलिखित सूत्र को लागू करके की जाती है:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

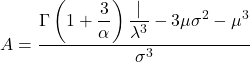
अंत में, वह सूत्र जो वेइबुल वितरण के कर्टोसिस गुणांक को निर्धारित करना संभव बनाता है वह निम्नलिखित है:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

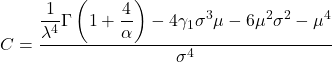
सोना

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

वेइबुल वितरण के अनुप्रयोग

वेइबुल वितरण में कई अनुप्रयोग हैं, जिनमें शामिल हैं:

व्यावहारिक आँकड़ों में, वेइबुल वितरण का उपयोग उत्तरजीविता विश्लेषण में किया जाता है।
इंजीनियरिंग में, वेइबुल वितरण का उपयोग विनिर्माण समय से संबंधित कार्यों को मॉडल करने के लिए किया जाता है।
रडार प्रणालियों में, प्राप्त सिग्नल के फैलाव का अनुकरण करने के लिए।
बीमा क्षेत्र में, दावों की सीमा का मॉडल तैयार करना।
उदाहरण के लिए, मौसम विज्ञान में, विभिन्न हवा की गति की आवृत्ति को मॉडल करना।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने