यह कैसे निर्धारित करें कि संभाव्यता वितरण वैध है या नहीं

संभाव्यता वितरण हमें संभाव्यता बताता है कि एक यादृच्छिक चर कुछ निश्चित मान लेता है।

संभाव्यता वितरण के वैध होने के लिए, इसे दो आवश्यकताओं को पूरा करना होगा:

1. प्रत्येक संभावना 0 और 1 के बीच होनी चाहिए।

2. संभावनाओं का योग 1 होना चाहिए।

यदि ये दो शर्तें पूरी होती हैं, तो संभाव्यता वितरण वैध है।

निम्नलिखित उदाहरण दिखाते हैं कि कैसे जांचें कि विभिन्न संभाव्यता वितरण वैध हैं या नहीं।

उदाहरण 1: फुटबॉल मैच में गोल किये गये

निम्नलिखित संभाव्यता वितरण इस संभावना को दर्शाता है कि एक निश्चित फुटबॉल टीम एक मैच में एक निश्चित संख्या में गोल करेगी:

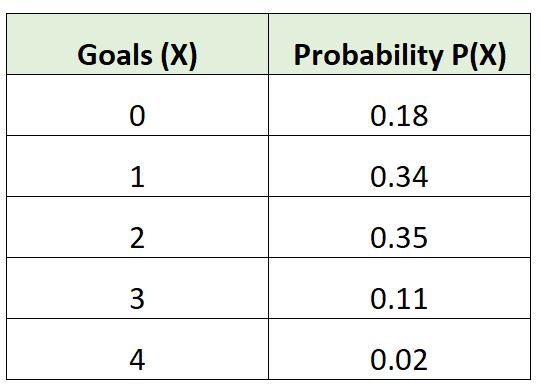
आइए देखें कि क्या यह संभाव्यता वितरण वैध होने के लिए दोनों आवश्यकताओं को पूरा करता है:

1. प्रत्येक संभावना 0 और 1 के बीच होनी चाहिए।

हम देख सकते हैं कि प्रत्येक व्यक्तिगत संभावना 0 और 1 के बीच है।

2. संभावनाओं का योग 1 होना चाहिए।

हम देख सकते हैं कि संभावनाओं का योग 1 तक पहुंचता है:

योग = 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1

दोनों शर्तें पूरी होती हैं, इसलिए यह संभाव्यता वितरण मान्य है।

उदाहरण 2: एक महीने में की गई बिक्री

निम्नलिखित संभाव्यता वितरण इस संभावना को दर्शाता है कि कोई दिया गया विक्रेता आने वाले महीने में एक निश्चित संख्या में बिक्री करेगा:

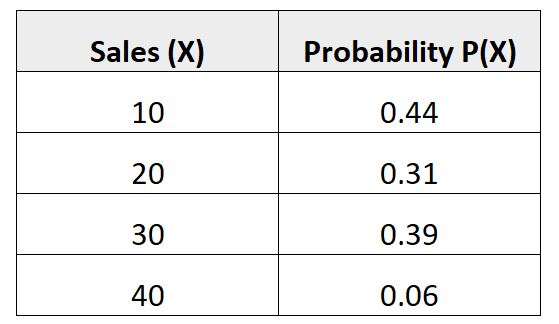
आइए देखें कि क्या यह संभाव्यता वितरण वैध होने के लिए दोनों आवश्यकताओं को पूरा करता है:

1. प्रत्येक संभावना 0 और 1 के बीच होनी चाहिए।

हम देख सकते हैं कि प्रत्येक व्यक्तिगत संभावना 0 और 1 के बीच है।

2. संभावनाओं का योग 1 होना चाहिए।

हम देखते हैं कि संभावनाओं का योग 1 तक नहीं जुड़ता:

योग = 0.44 + 0.31 + 0.39 + 0.06 = 1.2

दोनों शर्तें पूरी नहीं हुई हैं और इसलिए यह संभाव्यता वितरण अमान्य है।

उदाहरण 3: बैटरी विफलताओं की संख्या

निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि किसी दिए गए वाहन को 10 साल की अवधि में एक निश्चित संख्या में बैटरी विफलताओं का अनुभव होगा:

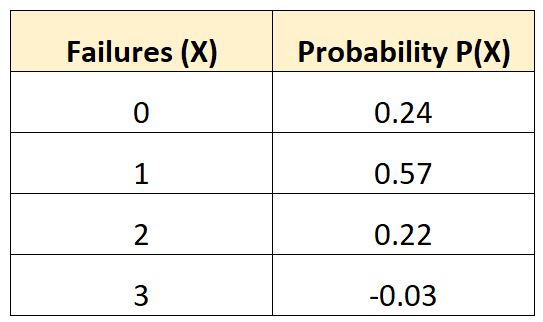
आइए देखें कि क्या यह संभाव्यता वितरण वैध होने के लिए दोनों आवश्यकताओं को पूरा करता है:

1. प्रत्येक संभावना 0 और 1 के बीच होनी चाहिए।

हम देख सकते हैं कि प्रत्येक व्यक्तिगत संभावना 0 और 1 के बीच नहीं है।

तालिका में अंतिम संभावना एक ऋणात्मक मान है।

2. संभावनाओं का योग 1 होना चाहिए।

हम देख सकते हैं कि संभावनाओं का योग 1 तक पहुंचता है:

योग = 0.24 + 0.57 + 0.22 – 0.03 = 1

दोनों शर्तें पूरी नहीं हुई हैं और इसलिए यह संभाव्यता वितरण अमान्य है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल संभाव्यता वितरण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

संभाव्यता वितरण का माध्य कैसे ज्ञात करें
संभाव्यता वितरण का प्रसरण कैसे ज्ञात करें
संभाव्यता वितरण का मानक विचलन कैसे ज्ञात करें