शिक्षा में सांख्यिकी का महत्व (उदाहरण सहित)

सांख्यिकी का क्षेत्र डेटा के संग्रह, विश्लेषण, व्याख्या और प्रस्तुति से संबंधित है।

शैक्षिक संदर्भ में, सांख्यिकी निम्नलिखित कारणों से महत्वपूर्ण हैं:

कारण 1 : सांख्यिकी शिक्षकों को वर्णनात्मक सांख्यिकी का उपयोग करके छात्रों के प्रदर्शन को समझने की अनुमति देती है।

कारण 2 : सांख्यिकी शिक्षकों को डेटा विज़ुअलाइज़ेशन का उपयोग करके छात्रों के प्रदर्शन में रुझान देखने की अनुमति देती है।

कारण 3 : सांख्यिकी शिक्षकों को परिकल्पना परीक्षण का उपयोग करके विभिन्न शिक्षण विधियों की तुलना करने की अनुमति देती है।

इस लेख के शेष भाग में, हम इनमें से प्रत्येक कारण का विकास करेंगे।

कारण 1: वर्णनात्मक आँकड़ों का उपयोग करके छात्र के प्रदर्शन को समझें

डेटा का वर्णन करने के लिए वर्णनात्मक सांख्यिकी का उपयोग किया जाता है।

शैक्षिक संदर्भ में, एक शिक्षक अपनी कक्षा में छात्रों के लिए निम्नलिखित वर्णनात्मक आंकड़ों की गणना कर सकता है:

• किसी दी गई परीक्षा में औसत अंक.
• किसी निश्चित परीक्षा में प्राप्तांकों का मानक विचलन।
• किसी दी गई परीक्षा में प्राप्तांकों की सीमा.
• एक निश्चित परीक्षा उत्तीर्ण करने वाले विद्यार्थियों का प्रतिशत.
• किसी दी गई परीक्षा के परिणाम का 90वां प्रतिशत।

इन मापों के लिए धन्यवाद, शिक्षक किसी दी गई परीक्षा में अपनी कक्षा के छात्रों के परिणामों को बेहतर ढंग से समझ सकता है।

फिर वह निर्णय ले सकती है कि यदि बहुत कम छात्र परीक्षा उत्तीर्ण करते हैं तो अपनी शिक्षण पद्धति को बदलना है या संभवतः खराब परीक्षा परिणाम वाले छात्रों को अतिरिक्त शिक्षण के अवसर प्रदान करना है, आदि।

नोट : इस प्रकार के वर्णनात्मक सांख्यिकी का उपयोग शिक्षा के सभी स्तरों पर किया जाता है। उदाहरण के लिए, एक प्रिंसिपल पूरे स्कूल में छात्रों के टेस्ट स्कोर की निगरानी के लिए वर्णनात्मक आंकड़ों का उपयोग कर सकता है। राज्य का शिक्षा विभाग पूरे राज्य में छात्रों के परीक्षण स्कोर की निगरानी के लिए वर्णनात्मक आंकड़ों का भी उपयोग कर सकता है।

कारण 2: डेटा विज़ुअलाइज़ेशन का उपयोग करके रुझानों का पता लगाएं

शिक्षा में सांख्यिकी का उपयोग करने का एक अन्य सामान्य तरीका लाइन ग्राफ़, हिस्टोग्राम, बॉक्सप्लॉट, पाई चार्ट और अन्य ग्राफ़ जैसे डेटा की कल्पना करना है।

इस प्रकार के चार्ट का उपयोग अक्सर शिक्षकों को कक्षा के प्रदर्शन और व्यक्तिगत छात्र प्रदर्शन में रुझान जानने में मदद करने के लिए किया जाता है।

उदाहरण के लिए, मान लीजिए कि एक शिक्षक पूरे वर्ष के औसत परीक्षा स्कोर को देखने के लिए निम्नलिखित बार चार्ट बनाता है:

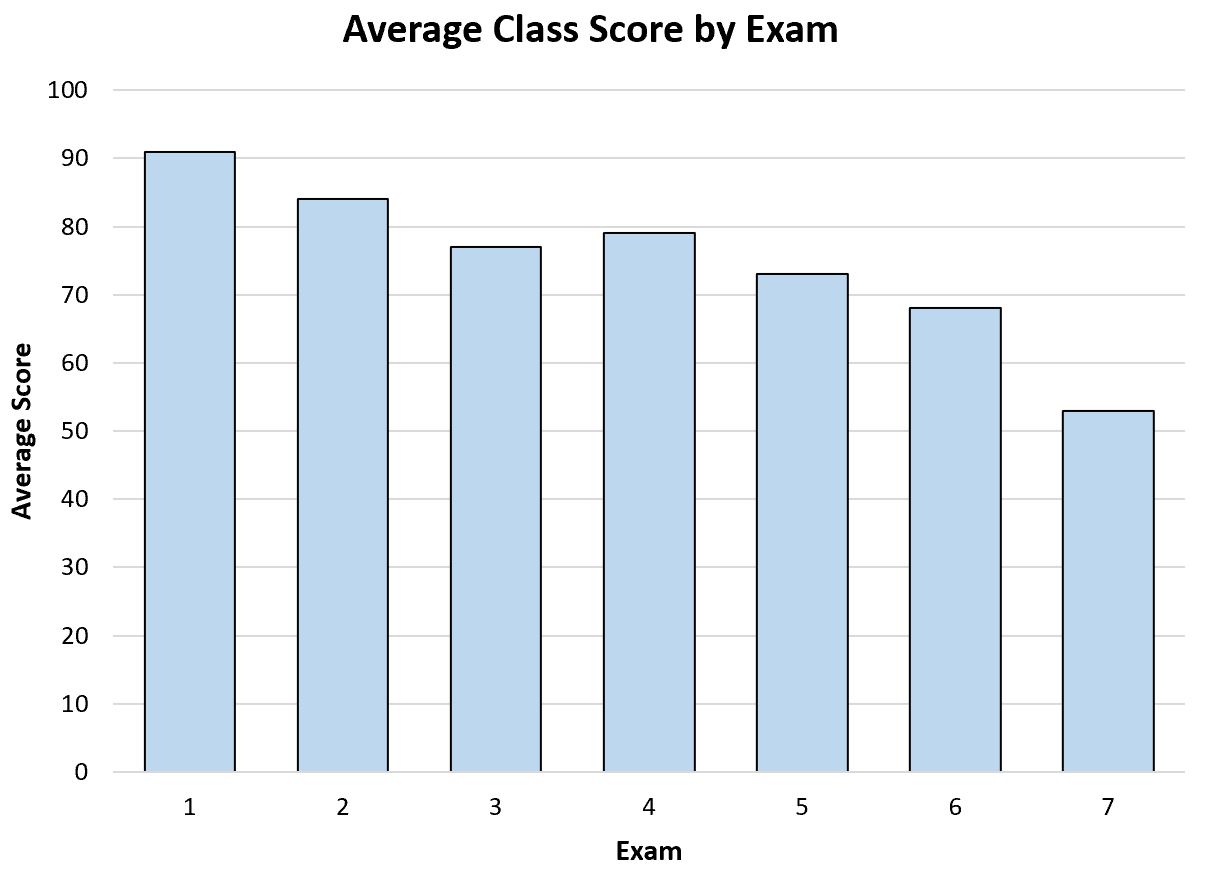
इस बार ग्राफ को देखकर ही शिक्षक यह देख पाएंगे कि उनकी कक्षा में छात्रों का औसत टेस्ट स्कोर साल भर में धीरे-धीरे कम हो रहा है।

इससे शिक्षक को अपनी शिक्षण विधियों में सुधार करने की अनुमति मिल सकती है या शायद वह अपने छात्रों को उनकी शिक्षण विधियों आदि पर उनकी राय पूछने के लिए एक सर्वेक्षण दे सकता है।

कारण 3: परिकल्पना परीक्षण का उपयोग करके शिक्षण विधियों की तुलना करें

सांख्यिकी का प्रयोग शिक्षा में परिकल्पना परीक्षण के रूप में भी किया जाता है।

ये ऐसे परीक्षण हैं जिनका उपयोग शिक्षक यह निर्धारित करने के लिए कर सकते हैं कि विभिन्न शिक्षण विधियों के बीच सांख्यिकीय महत्व है या नहीं।

उदाहरण के लिए, मान लीजिए कि एक शिक्षक यह निर्धारित करना चाहता है कि क्या एक निश्चित पाठ्यक्रम परीक्षण स्कोर को प्रभावित करता है। इसका परीक्षण करने के लिए, वह प्री-टेस्ट लेने के लिए यादृच्छिक रूप से 15 छात्रों का चयन करता है । फिर वह प्रत्येक छात्र से एक महीने के लिए पाठ्यक्रम का उपयोग करवाता है और उसके बाद समान कठिनाई का परीक्षण कराता है।

15 छात्रों में से प्रत्येक के परीक्षा परिणाम नीचे दिखाए गए हैं:

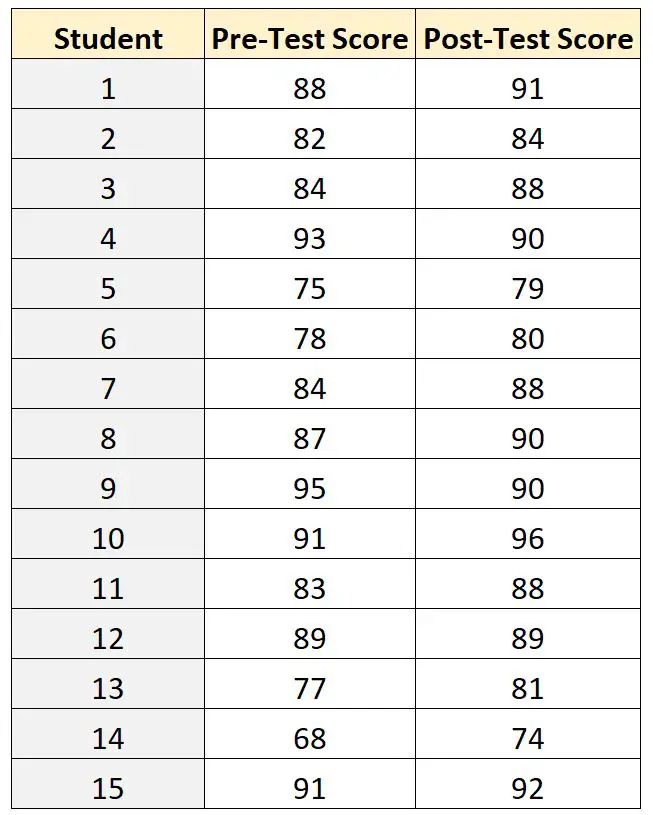
प्री-टेस्ट और पोस्ट-टेस्ट माध्य स्कोर के बीच अंतर की तुलना करने के लिए, शिक्षक युग्मित टी-टेस्ट नमूनों का उपयोग कर सकते हैं क्योंकि प्रत्येक छात्र के लिए, उनके प्री-टेस्ट स्कोर को उनके पोस्ट-टेस्ट स्कोर के साथ जोड़ा जा सकता है।

मान लीजिए कि प्रोफेसर इस युग्मित-नमूने टी-परीक्षण को करने के लिए सांख्यिकीय सॉफ़्टवेयर का उपयोग करता है और निम्नलिखित परिणाम प्राप्त करता है:

• टी-परीक्षण आँकड़ा: -2.97
• पी-वैल्यू: 0.0101

इस उदाहरण में, युग्मित नमूने टी-परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करते हैं:

• एच ₀ : औसत परीक्षण-पूर्व और परीक्षण-पश्चात अंक बराबर हैं
• एच _ए : परीक्षण-पूर्व और परीक्षण-पश्चात् औसत अंक समान नहीं हैं

चूँकि पी-मान ( 0.0101 ) 0.05 से कम है, हम शून्य परिकल्पना को अस्वीकार करते हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि अध्ययन कार्यक्रम में भाग लेने से पहले और बाद में छात्रों के लिए औसत परीक्षण स्कोर अलग-अलग है।

नोट : यह शिक्षा में प्रयुक्त परिकल्पना परीक्षण का सिर्फ एक उदाहरण है। अन्य सामान्य परीक्षणों में एक-नमूना टी-परीक्षण , दो-नमूना टी-परीक्षण , एक-तरफ़ा एनोवा और दो-तरफ़ा एनोवा शामिल हैं।

अतिरिक्त संसाधन

निम्नलिखित लेख अन्य क्षेत्रों में सांख्यिकी के महत्व को समझाते हैं:

व्यवसायों में सांख्यिकी का महत्व
अर्थशास्त्र में सांख्यिकी का महत्व
स्वास्थ्य देखभाल में सांख्यिकी का महत्व