संतुलित सटीकता क्या है? (परिभाषा & #038; उदाहरण)

संतुलित सटीकता एक मीट्रिक है जिसका उपयोग हम वर्गीकरण मॉडल के प्रदर्शन का मूल्यांकन करने के लिए कर सकते हैं।

इसकी गणना इस प्रकार की जाती है:

संतुलित सटीकता = (संवेदनशीलता + विशिष्टता) / 2

सोना:

• संवेदनशीलता : “सच्ची सकारात्मक दर” – सकारात्मक मामलों का प्रतिशत जो मॉडल पता लगाने में सक्षम है।
• विशिष्टता : “सच्ची नकारात्मक दर” – नकारात्मक मामलों का प्रतिशत जो मॉडल पता लगाने में सक्षम है।

यह मीट्रिक विशेष रूप से तब उपयोगी होती है जब दो वर्ग असंतुलित होते हैं, अर्थात, एक वर्ग दूसरे की तुलना में बहुत अधिक दिखाई देता है।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में संतुलित सटीकता की गणना कैसे की जाती है और यह दर्शाता है कि यह इतनी उपयोगी मीट्रिक क्यों है।

उदाहरण: संतुलित परिशुद्धता की गणना

मान लीजिए कि एक खेल विश्लेषक यह अनुमान लगाने के लिए एक लॉजिस्टिक रिग्रेशन मॉडल का उपयोग करता है कि 400 अलग-अलग कॉलेज बास्केटबॉल खिलाड़ियों को एनबीए में शामिल किया जाएगा या नहीं।

निम्नलिखित भ्रम मैट्रिक्स मॉडल द्वारा की गई भविष्यवाणियों का सारांश प्रस्तुत करता है:

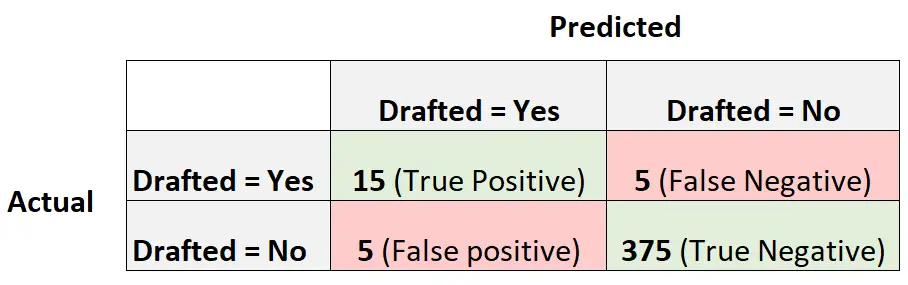
मॉडल की संतुलित सटीकता की गणना करने के लिए, हम पहले संवेदनशीलता और विशिष्टता की गणना करेंगे:

• संवेदनशीलता : “सच्ची सकारात्मक दर” = 15 / (15 + 5) = 0.75
• विशिष्टता : “सच्ची नकारात्मक दर” = 375 / (375 + 5) = 0.9868

फिर हम संतुलित परिशुद्धता की गणना इस प्रकार कर सकते हैं:

• संतुलित सटीकता = (संवेदनशीलता + विशिष्टता) / 2
• संतुलित सटीकता = (0.75 + 9868)/2
• संतुलित सटीकता = 0.8684

मॉडल की संतुलित सटीकता 0.8684 निकली।

ध्यान दें कि संतुलित परिशुद्धता 1 के जितनी करीब होगी, मॉडल उतना ही अधिक अवलोकनों को सही ढंग से वर्गीकृत करने में सक्षम होगा।

इस उदाहरण में, संतुलित सटीकता काफी अधिक है, जो हमें बताती है कि लॉजिस्टिक रिग्रेशन मॉडल यह भविष्यवाणी करने का बहुत अच्छा काम कर रहा है कि कॉलेज के खिलाड़ियों को एनबीए में शामिल किया जाएगा या नहीं।

इस परिदृश्य में, चूंकि कक्षाएं बहुत असंतुलित हैं (20 खिलाड़ियों को ड्राफ्ट किया गया था और 380 खिलाड़ियों को नहीं चुना गया था), संतुलित सटीकता हमें समग्र सटीकता माप की तुलना में मॉडल प्रदर्शन की अधिक यथार्थवादी तस्वीर देती है।

उदाहरण के लिए, हम मॉडल सटीकता की गणना इस प्रकार करेंगे:

• सटीकता = (टीपी + टीएन) / (टीपी + टीएन + एफपी + एफएन)
• सटीकता = (15 + 375) / (15 + 375 + 5 + 5)
• सटीकता = 0.975

मॉडल की सटीकता 0.975 है, जो बहुत अधिक लगती है।

हालाँकि, एक ऐसे मॉडल पर विचार करें जो केवल यह भविष्यवाणी करता है कि प्रत्येक खिलाड़ी बिना ड्राफ्ट के चुना जाएगा। इसकी सटीकता 380/400 = 0.95 होगी। यह हमारे मॉडल की सटीकता से थोड़ा ही कम है।

0.8684 का संतुलित सटीकता स्कोर हमें दोनों वर्गों की भविष्यवाणी करने की मॉडल की क्षमता का बेहतर विचार देता है।

दूसरे शब्दों में, यह हमें मॉडल की भविष्यवाणी करने की क्षमता का बेहतर विचार देता है कि कौन से खिलाड़ी बिना ड्राफ्ट के जाएंगे और कौन से।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर में भ्रम मैट्रिक्स कैसे बनाया जाए:

एक्सेल में कन्फ्यूजन मैट्रिक्स कैसे बनाएं
आर में कन्फ्यूजन मैट्रिक्स कैसे बनाएं
पायथन में कन्फ्यूजन मैट्रिक्स कैसे बनाएं