संबंधी मानक विचलन
यह आलेख बताता है कि सापेक्ष मानक विचलन की गणना कैसे करें। आपको पता चलेगा कि सापेक्ष मानक विचलन क्या है, इसका सूत्र क्या है, साथ ही चरण दर चरण हल किया गया अभ्यास भी।
सापेक्ष मानक विचलन क्या है?
सापेक्ष मानक विचलन एक सांख्यिकीय माप है जो किसी डेटा सेट के माध्य के सापेक्ष फैलाव को इंगित करता है। सापेक्ष मानक विचलन की गणना डेटा के मानक विचलन को उसके माध्य से विभाजित करके की जाती है।
सापेक्ष मानक विचलन को प्रतिशत के रूप में व्यक्त किया जाता है और इसका मान हमेशा सकारात्मक रहेगा।
सापेक्ष मानक विचलन की व्याख्या का उपयोग डेटा नमूने के फैलाव को दिखाने के लिए किया जाता है। सापेक्ष मानक विचलन का मान जितना बड़ा होगा, डेटा उतना ही अधिक बिखरा हुआ होगा। और सापेक्ष मानक विचलन जितना छोटा होगा, डेटा अपने माध्य के उतना ही करीब होगा।
आम तौर पर, संक्षिप्त नाम आरएसडी का उपयोग सापेक्ष मानक विचलन के प्रतीक के रूप में किया जाता है।
सापेक्ष मानक विचलन सूत्र
सापेक्ष मानक विचलन मानक विचलन को 100 से गुणा किए गए माध्य से विभाजित करने के बराबर है। इसलिए, सापेक्ष मानक विचलन की गणना करने के लिए, आपको पहले मानक विचलन और अंकगणितीय माध्य निर्धारित करना होगा, फिर दो सांख्यिकीय मापों को विभाजित करना होगा और अंत में 100 से गुणा करना होगा।
दूसरे शब्दों में, सापेक्ष मानक विचलन का सूत्र है:
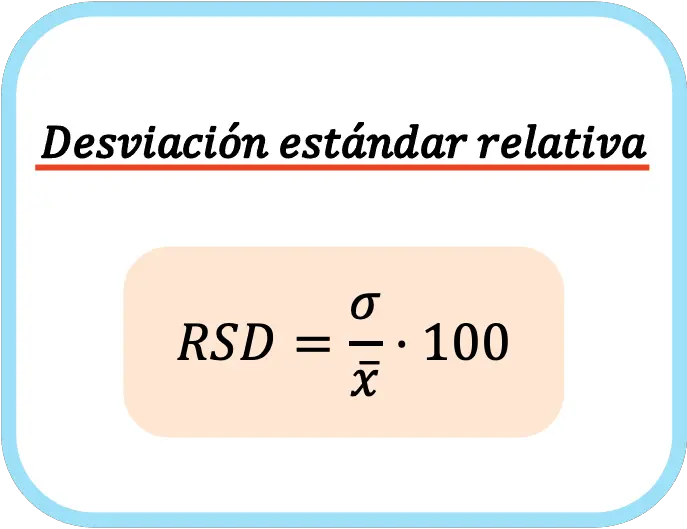
सापेक्ष मानक विचलन की गणना करते समय, मान को प्रतिशत के रूप में व्यक्त करने के लिए इसे एक सौ से गुणा किया जाता है।
सापेक्ष मानक विचलन की गणना का उदाहरण
सापेक्ष मानक विचलन की परिभाषा और उसके सूत्र की समीक्षा करने के बाद, आप नीचे एक ठोस उदाहरण देख सकते हैं कि सापेक्ष मानक विचलन की गणना कैसे की जाती है।
- निम्नलिखित सांख्यिकीय डेटा सेट के सापेक्ष मानक विचलन की गणना करें:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
सबसे पहले, हमें डेटा का मानक विचलन ज्ञात करना होगा:
![]()
दूसरा, हम डेटा के अंकगणितीय माध्य की गणना करते हैं:
![]()
एक बार जब हम डेटा श्रृंखला के मानक विचलन और अंकगणितीय माध्य को जान लेते हैं, तो हम सापेक्ष मानक विचलन सूत्र का उपयोग करते हैं।
![]()
और अंत में, हम परिकलित मानों को सूत्र में प्रतिस्थापित करते हैं और सापेक्ष मानक विचलन की गणना करते हैं:
![]()