संभाव्यता वितरण का माध्य कैसे ज्ञात करें: उदाहरणों के साथ

संभाव्यता वितरण हमें संभाव्यता बताता है कि एक यादृच्छिक चर कुछ निश्चित मान लेता है।

उदाहरण के लिए, निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि एक निश्चित फुटबॉल टीम किसी दिए गए मैच में एक निश्चित संख्या में गोल करेगी:

ध्यान दें: वैध संभाव्यता वितरण में संभावनाओं का योग हमेशा 1 होगा। हम पुष्टि कर सकते हैं कि यह संभाव्यता वितरण वैध है: 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1।

संभाव्यता वितरण का माध्य (जिसे कभी-कभी “अपेक्षित मान” भी कहा जाता है) खोजने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

 Mean (Or "Expected Value") of a Probability Distribution:

μ = Σx * P(x)

where:
•x: Data value
    •P(x): Probability of value

उदाहरण के लिए, फुटबॉल टीम के लिए हमारे संभाव्यता वितरण पर विचार करें:

फ़ुटबॉल टीम के गोलों की औसत संख्या की गणना इस प्रकार की जाएगी:

μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 गोल।

निम्नलिखित उदाहरण दिखाते हैं कि कुछ अन्य परिदृश्यों में संभाव्यता वितरण के औसत की गणना कैसे करें।

उदाहरण 1: वाहन खराब होने की औसत संख्या

निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि किसी दिए गए वाहन को 10 साल की अवधि में एक निश्चित संख्या में बैटरी विफलताओं का अनुभव होगा:

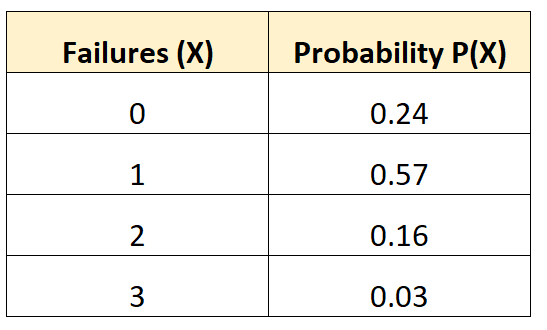
प्रश्न: इस वाहन के लिए अपेक्षित ब्रेकडाउन की औसत संख्या क्या है?

समाधान: अपेक्षित विफलताओं की औसत संख्या की गणना निम्नानुसार की जाती है:

μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98 विफलताएँ।

उदाहरण 2: जीत की औसत संख्या

निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि एक दी गई बास्केटबॉल टीम एक टूर्नामेंट में एक निश्चित संख्या में गेम जीतेगी:

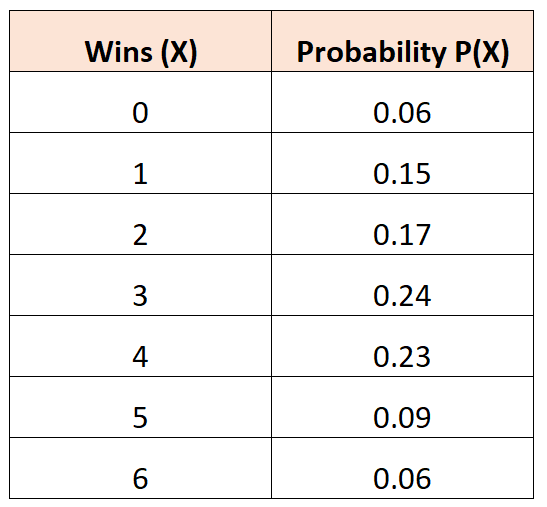
प्रश्न: इस टीम के लिए अपेक्षित जीत की औसत संख्या क्या है?

समाधान: अपेक्षित जीत की औसत संख्या की गणना निम्नानुसार की जाती है:

μ = 0*0.06 + 1*0.15 + 2*0.17 + 3*0.24 + 4*0.23 + 5*0.09 + 6*0.06 = 2.94 जीत।

उदाहरण 3: बिक्री की औसत संख्या

निम्नलिखित संभाव्यता वितरण हमें यह संभाव्यता बताता है कि कोई विक्रेता आने वाले महीने में एक निश्चित संख्या में बिक्री करेगा:

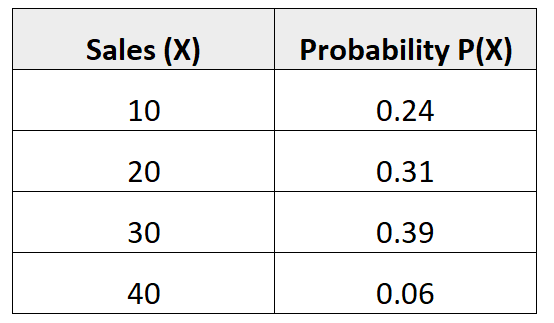
प्रश्न: आने वाले महीने में इस विक्रेता के लिए अपेक्षित बिक्री की औसत संख्या क्या है?

समाधान: अपेक्षित बिक्री की औसत संख्या की गणना निम्नानुसार की जाती है:

μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7 गंदा।

बोनस: संभाव्यता वितरण कैलकुलेटर

आप किसी भी संभाव्यता वितरण के माध्य की स्वचालित रूप से गणना करने के लिए इस कैलकुलेटर का उपयोग कर सकते हैं।