संभाव्यता वितरण के विचरण की गणना कैसे करें

संभाव्यता वितरण हमें संभाव्यता बताता है कि एक यादृच्छिक चर कुछ निश्चित मान लेता है।

उदाहरण के लिए, निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि एक निश्चित फुटबॉल टीम किसी दिए गए मैच में एक निश्चित संख्या में गोल करेगी:

संभाव्यता वितरण का प्रसरण ज्ञात करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

σ ² = Σ(x _i -μ) ² * P(x _i )

सोना:

• x _i : ^ith मान
• μ: वितरण का माध्य
• P(x _i ): ^iवें मान की प्रायिकता

उदाहरण के लिए, फुटबॉल टीम के लिए हमारे संभाव्यता वितरण पर विचार करें:

फ़ुटबॉल टीम के गोलों की औसत संख्या की गणना इस प्रकार की जाएगी:

μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 गोल।

फिर हम विचरण की गणना इस प्रकार कर सकते हैं:

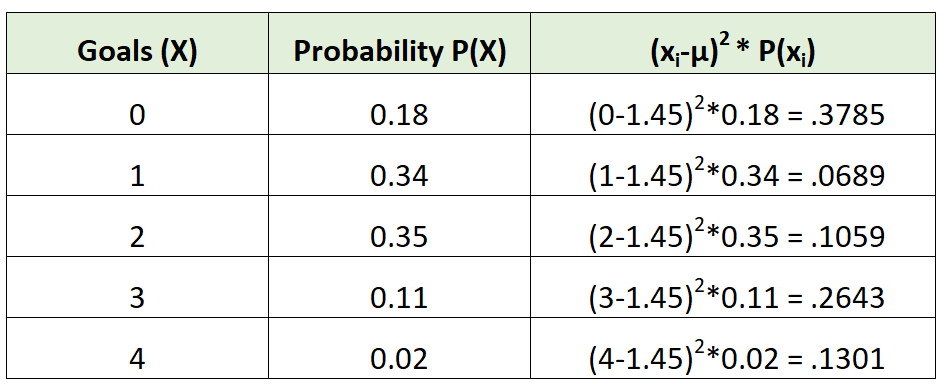
भिन्नता केवल तीसरे कॉलम में मानों का योग है। तो, हम इसकी गणना इस प्रकार करेंगे:

^σ2 = 0.3785 + 0.0689 + 0.1059 + 0.2643 + 0.1301 = 0.9475

निम्नलिखित उदाहरण दिखाते हैं कि कुछ अन्य परिदृश्यों में संभाव्यता वितरण के विचरण की गणना कैसे करें।

उदाहरण 1: वाहन खराब होने में भिन्नता

निम्नलिखित संभाव्यता वितरण हमें इस संभावना को बताता है कि किसी दिए गए वाहन को 10 साल की अवधि में एक निश्चित संख्या में बैटरी विफलताओं का अनुभव होगा:

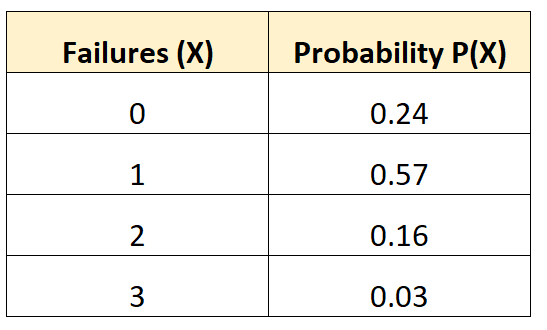
इस संभाव्यता वितरण के विचरण को खोजने के लिए, हमें पहले अपेक्षित विफलताओं की औसत संख्या की गणना करने की आवश्यकता है:

μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98 विफलताएँ।

फिर हम विचरण की गणना इस प्रकार कर सकते हैं:

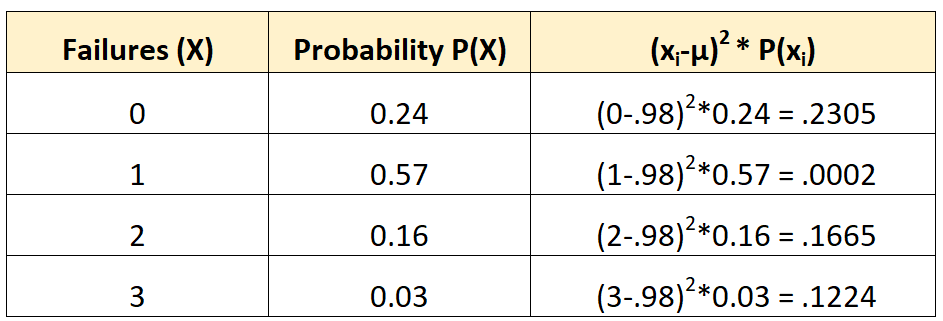
प्रसरण तीसरे स्तंभ में मानों का योग है। तो, हम इसकी गणना इस प्रकार करेंगे:

^σ2 = 0.2305 + 0.0002 + 0.1665 + 0.1224 = 0.5196

उदाहरण 2: बिक्री भिन्नता

निम्नलिखित संभाव्यता वितरण हमें यह संभाव्यता बताता है कि कोई विक्रेता आने वाले महीने में एक निश्चित संख्या में बिक्री करेगा:

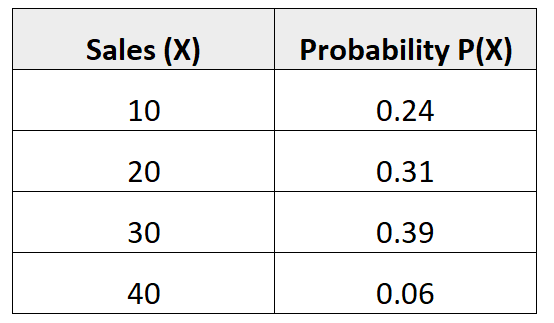
इस संभाव्यता वितरण के विचरण को खोजने के लिए, हमें पहले अपेक्षित बिक्री की औसत संख्या की गणना करने की आवश्यकता है:

μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7 गंदा।

फिर हम विचरण की गणना इस प्रकार कर सकते हैं:

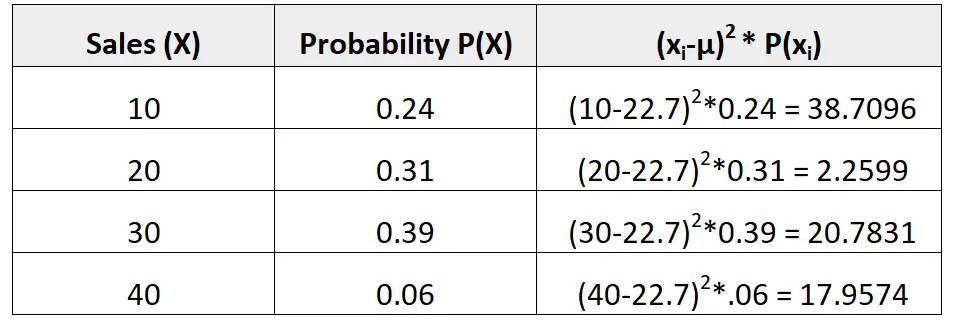
प्रसरण तीसरे स्तंभ में मानों का योग है। तो, हम इसकी गणना इस प्रकार करेंगे:

^σ2 = 38.7096 + 2.2599 + 20.7831 + 17.9574 = 79.71

ध्यान दें कि हम इस वितरण के विचरण की स्वचालित रूप से गणना करने के लिए संभाव्यता वितरण कैलकुलेटर का भी उपयोग कर सकते हैं:

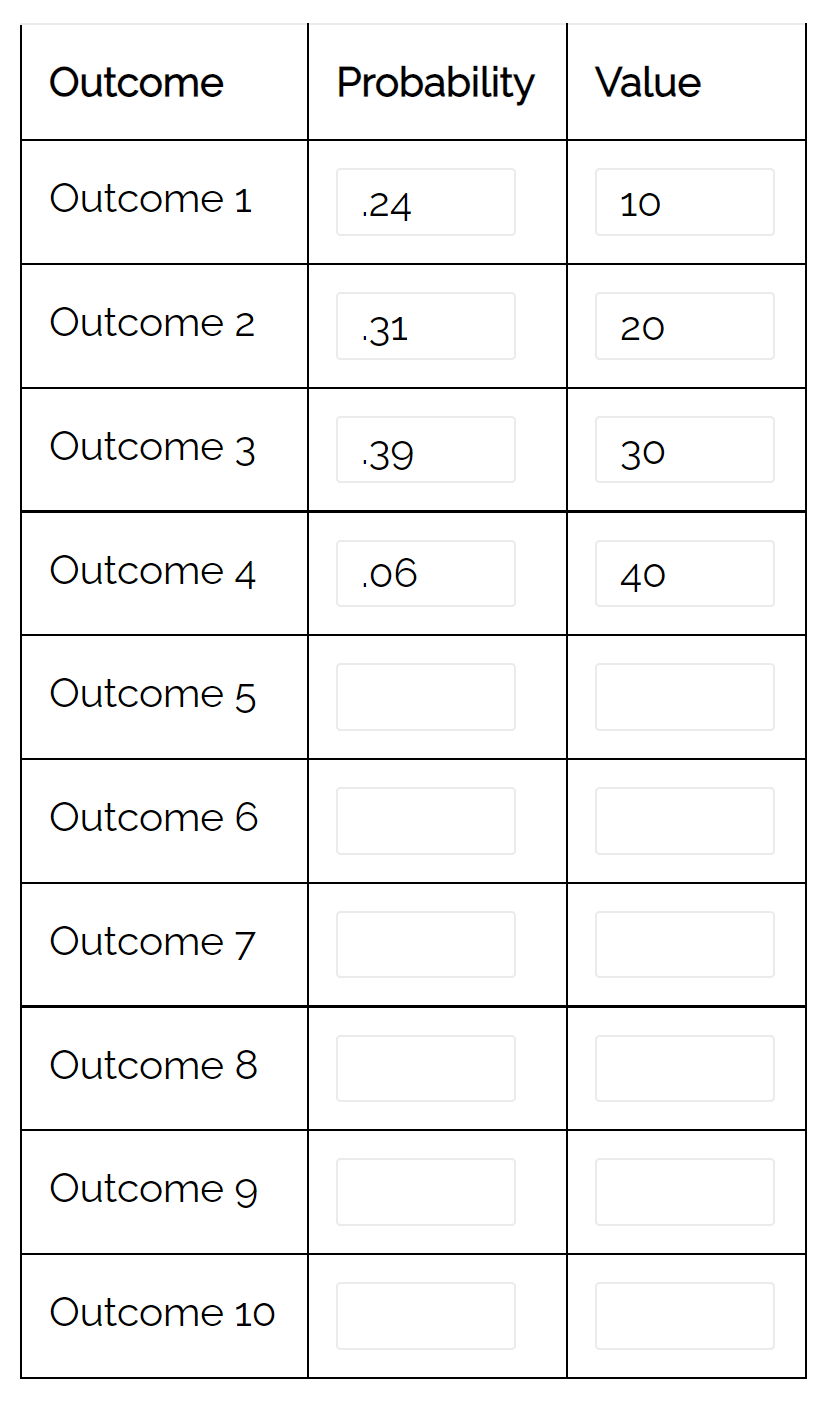
अंतर 79.71 है. यह उस मान से मेल खाता है जिसकी हमने मैन्युअल रूप से गणना की थी।