संभाव्यता फलन

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि संभाव्यता फलन क्या हैं। इस प्रकार, आपको संभाव्यता फलन का अर्थ, उसके गुण और संभाव्यता फलन की गणना का एक ठोस उदाहरण मिलेगा। इसके अतिरिक्त, संभाव्यता फ़ंक्शन और अन्य प्रकार के संभाव्य कार्यों के बीच अंतर प्रस्तुत किए जाते हैं।

संभाव्यता फलन क्या है?

संभाव्यता फ़ंक्शन , जिसे संभाव्यता द्रव्यमान फ़ंक्शन भी कहा जाता है, एक गणितीय फ़ंक्शन है जो इस संभावना का वर्णन करता है कि एक अलग यादृच्छिक चर एक निश्चित मान लेता है।

अर्थात्, एक संभाव्यता फ़ंक्शन किसी असतत चर से जुड़ी संभाव्यता को किसी मान के बिल्कुल बराबर होने की संभावना लौटाता है।

$f(x)=P[X=x]$

उदाहरण के लिए, पासे को घुमाने पर किसी भी संख्या के लुढ़कने की संभावना 1/6 है (एक पासे की छह भुजाएँ होती हैं), इसलिए इस नमूना स्थान से जुड़ा संभाव्यता फ़ंक्शन n के लिए 1/6 के बराबर होगा, चाहे कोई भी मूल्य हो।

संभाव्यता फलन के गुण

संभाव्यता कार्यों में निम्नलिखित गुण होते हैं:

संभाव्यताएँ ऋणात्मक नहीं हो सकतीं, इसलिए x के किसी भी मान के लिए संभाव्यता फलन शून्य या धनात्मक है।

$f(x)\geq 0$

इसी तरह, अधिकतम संभावना एकता है, जिसका अर्थ है कि घटना हमेशा घटित होगी। इसलिए, संभाव्यता फ़ंक्शन का अधिकतम मान 1 के बराबर है।

$f(x)\leq 1$

अंत में, संभाव्यता फ़ंक्शन के सभी मानों का योग 1 देता है, क्योंकि यह नमूना स्थान में सभी संभावनाओं का योग है।

$\displaystyle \sum_{i=1}^{+\infty}f(x_i)=\sum_{i=1}^{+\infty}p_i=1$

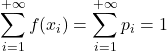
संभाव्यता फलन उदाहरण

अब जब हम संभाव्यता फ़ंक्शन की परिभाषा और विशेषताओं को जानते हैं, तो आइए इस प्रकार के संभाव्य फ़ंक्शन का एक उदाहरण देखें।

चार स्वतंत्र सिक्के उछालकर 0, 1, 2, 3 और 4 बार शीर्ष प्राप्त करने की संभावनाओं की गणना करें। इसके बाद, पाए गए संभाव्यता फ़ंक्शन का ग्राफ़ बनाएं।

सबसे पहले, हमें चित आने की संभावनाओं की गणना करनी चाहिए, ऐसा करने के लिए, हमें संभावित मामलों को कुल मामलों की संख्या से विभाजित करना होगा। आप सभी संभावनाओं की गणना निम्न तालिका में देख सकते हैं:

और एक बार जब हमने सभी संभावनाओं की गणना कर ली है, तो हम एक ग्राफ पर संभाव्यता फ़ंक्शन के मूल्यों का प्रतिनिधित्व कर सकते हैं:

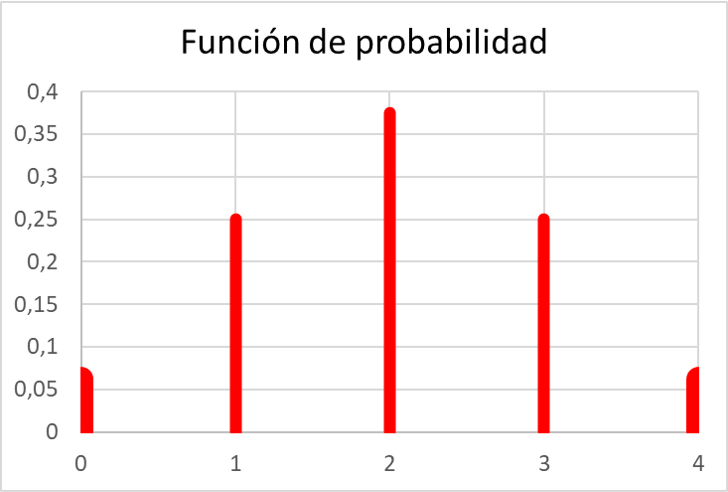
जैसा कि आप देख सकते हैं, अभ्यास में संभाव्य फ़ंक्शन संभाव्यता फ़ंक्शन के सभी गुणों को पूरा करता है, क्योंकि इसके सभी मान 0 और 1 के बीच हैं और, इसके अलावा, इसके सभी मानों का योग 1 के बराबर है।

संभाव्यता फलन और घनत्व फलन

इस खंड में हम संभाव्यता फ़ंक्शन और घनत्व फ़ंक्शन के बीच अंतर देखेंगे, क्योंकि वे दो प्रकार के संभाव्य फ़ंक्शन हैं जिनका उद्देश्य एक ही है लेकिन विभिन्न मामलों में उपयोग किया जाता है।

संभाव्यता फ़ंक्शन और घनत्व फ़ंक्शन के बीच का अंतर चर का प्रकार है जिसके लिए संभावनाएं वर्णित हैं। संभाव्यता फ़ंक्शन का उपयोग असतत चर की संभावनाओं को परिभाषित करने के लिए किया जाता है, जबकि घनत्व फ़ंक्शन का उपयोग निरंतर चर की संभावनाओं को परिभाषित करने के लिए किया जाता है।

इसलिए, चर के आधार पर, एक संभाव्यता फ़ंक्शन या घनत्व फ़ंक्शन का उपयोग किया जाता है।

घनत्व फ़ंक्शन के बारे में अधिक जानने के लिए, निम्नलिखित लिंक पर क्लिक करें:

➤ देखें: संभाव्यता घनत्व फ़ंक्शन

संभाव्यता फलन और वितरण फलन

संभाव्यता फलन और वितरण फलन के बीच का अंतर संभाव्यता का प्रकार है जिसे वे परिभाषित करते हैं। संभाव्यता फ़ंक्शन इस संभावना को इंगित करता है कि चर एक निश्चित मान लेता है, जबकि वितरण फ़ंक्शन चर की संचयी संभावना का वर्णन करता है।

इसलिए, वितरण फ़ंक्शन की गणना संभाव्यता फ़ंक्शन से की जाती है।

उदाहरण के तौर पर, निम्नलिखित लिंक में आप उपरोक्त अभ्यास में पाए गए संभाव्यता फ़ंक्शन के आधार पर, चार सिक्के उछालने से हेड प्राप्त करने के लिए वितरण फ़ंक्शन की गणना देख सकते हैं।

➤ देखें: वितरण फ़ंक्शन उदाहरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने