संयुक्त संभाव्यता वितरण क्या है?

दो-तरफा आवृत्ति तालिका एक तालिका है जो दो श्रेणीबद्ध चर के लिए आवृत्तियों (या “गणना”) को प्रदर्शित करती है।

उदाहरण के लिए, निम्नलिखित दो-तरफ़ा तालिका एक सर्वेक्षण के परिणाम दिखाती है जिसमें 100 लोगों से पूछा गया कि उन्हें कौन सा खेल पसंद है: बेसबॉल, बास्केटबॉल, या फ़ुटबॉल।

पंक्तियाँ उत्तरदाता का लिंग प्रदर्शित करती हैं और कॉलम उनके द्वारा चुने गए खेल को दर्शाते हैं:

इस उदाहरण में, दो चर हैं: खेल और लिंग।

एक संयुक्त संभाव्यता वितरण केवल उस संभाव्यता का वर्णन करता है कि कोई दिया गया व्यक्ति चर के लिए दो विशिष्ट मान लेता है।

शब्द “संयुक्त” इस तथ्य से आया है कि हम एक ही समय में दो चीजों के घटित होने की संभावना में रुचि रखते हैं।

उदाहरण के लिए, कुल 100 व्यक्तियों में से 13 पुरुष थे और उन्होंने बेसबॉल को अपने पसंदीदा खेल के रूप में चुना।

तो, हम कहेंगे कि संयुक्त संभावना कि कोई व्यक्ति पुरुष है और बेसबॉल को अपने पसंदीदा खेल के रूप में चुनता है 13/100 = 0.13 या 13% है।

गणितीय संकेतन में लिखा गया:

पी(लिंग = पुरुष, खेल = बेसबॉल) = 13/100 = 0.13 ।

हम संपूर्ण संयुक्त संभाव्यता वितरण की गणना के लिए इस प्रक्रिया का उपयोग कर सकते हैं:

• पी (लिंग = पुरुष, खेल = बेसबॉल) = 13/100 = 0.13
• पी (लिंग = पुरुष, खेल = बास्केटबॉल) = 15/100 = 0.15
• पी (लिंग = पुरुष, खेल = फुटबॉल) = 20/100 = 0.20
• पी (लिंग = महिला, खेल = बेसबॉल) = 23/100 = 0.23
• पी (लिंग = महिला, खेल = बास्केटबॉल) = 16/100 = 0.16
• पी(लिंग = महिला, खेल = फुटबॉल) = 13/100 = 0.13

ध्यान दें कि संभावनाओं का योग 1 या 100% के बराबर है।

संयुक्त संभाव्यता वितरण का उपयोग क्यों करें?

संयुक्त संभाव्यता वितरण उपयोगी हैं क्योंकि हम अक्सर दो चर (जैसे खेल और लिंग) के लिए डेटा एकत्र करते हैं और दोनों चर से संबंधित प्रश्नों का उत्तर देना चाहते हैं।

उदाहरण के लिए, हम इस संभावना को समझना चाह सकते हैं कि किसी आबादी में कोई व्यक्ति पुरुष है और बेसबॉल को अपने पसंदीदा खेल के रूप में पसंद करता है।

या हमें इस संभावना को समझने में रुचि हो सकती है कि कोई व्यक्ति महिला है और फुटबॉल को अपने पसंदीदा खेल के रूप में पसंद करता है।

एक संयुक्त संभाव्यता वितरण हमें इन प्रश्नों का उत्तर देने में मदद कर सकता है।

संयुक्त संभाव्यता वितरण को बेहतर ढंग से समझने के लिए अभ्यास के रूप में निम्नलिखित उदाहरणों का उपयोग करें।

उदाहरण 1

निम्नलिखित दो-तरफा तालिका एक सर्वेक्षण के परिणाम प्रस्तुत करती है जिसमें 238 लोगों से पूछा गया कि उन्हें किस प्रकार की फिल्म पसंद है:

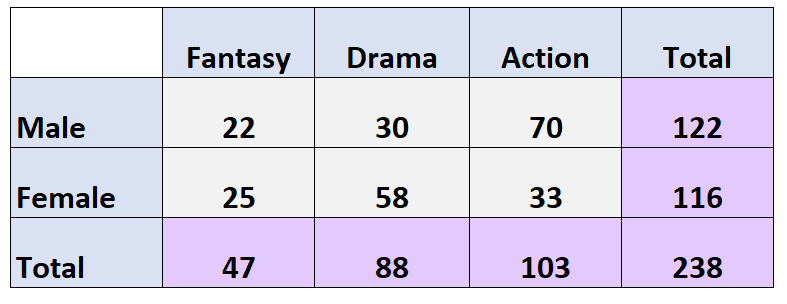
प्रश्न: इसकी क्या संभावना है कि कोई व्यक्ति महिला है और नाटक को अपनी पसंदीदा फिल्म शैली के रूप में पसंद करता है?

उत्तर: पी (लिंग = महिला, लिंग = नाटक) = 58/238 = 0.244 = 24.4%

उदाहरण 2

निम्नलिखित दो-तरफा तालिका एक कक्षा में 64 छात्रों के अध्ययन के घंटों की संख्या के आधार पर उनके परीक्षा स्कोर को दर्शाती है:

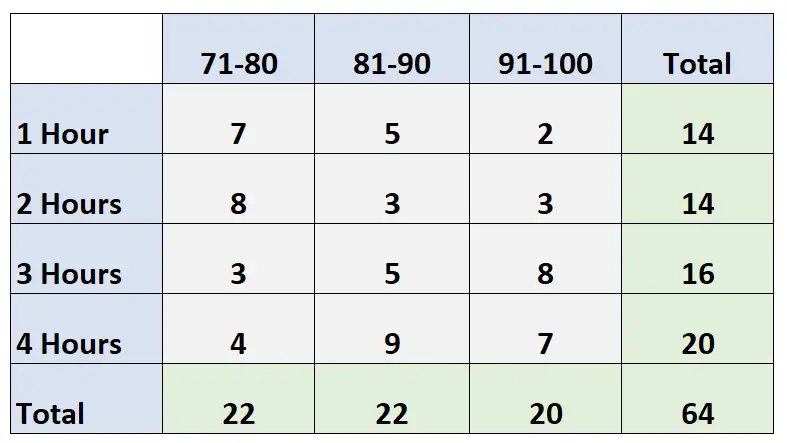
प्रश्न: इसकी क्या प्रायिकता है कि कोई व्यक्ति 2 घंटे पढ़ाई करता है और 91 और 100 के बीच ग्रेड प्राप्त करता है?

उत्तर: पी (अध्ययन = 2 घंटे, स्कोर = 91-100) = 3/64 = 0.047 = 4.7%

अतिरिक्त संसाधन

सीमांत वितरण क्या है?
दोहरी प्रविष्टि तालिका में सशर्त सापेक्ष आवृत्ति कैसे ज्ञात करें