समानांतर रूपों की विश्वसनीयता क्या है? (परिभाषा & #038; उदाहरण)

आंकड़ों में, समानांतर रूप विश्वसनीयता एक परीक्षण के दो समकक्ष रूपों के बीच सहसंबंध को मापती है।

समानांतर रूपों की विश्वसनीयता की गणना करने की प्रक्रिया इस प्रकार है:

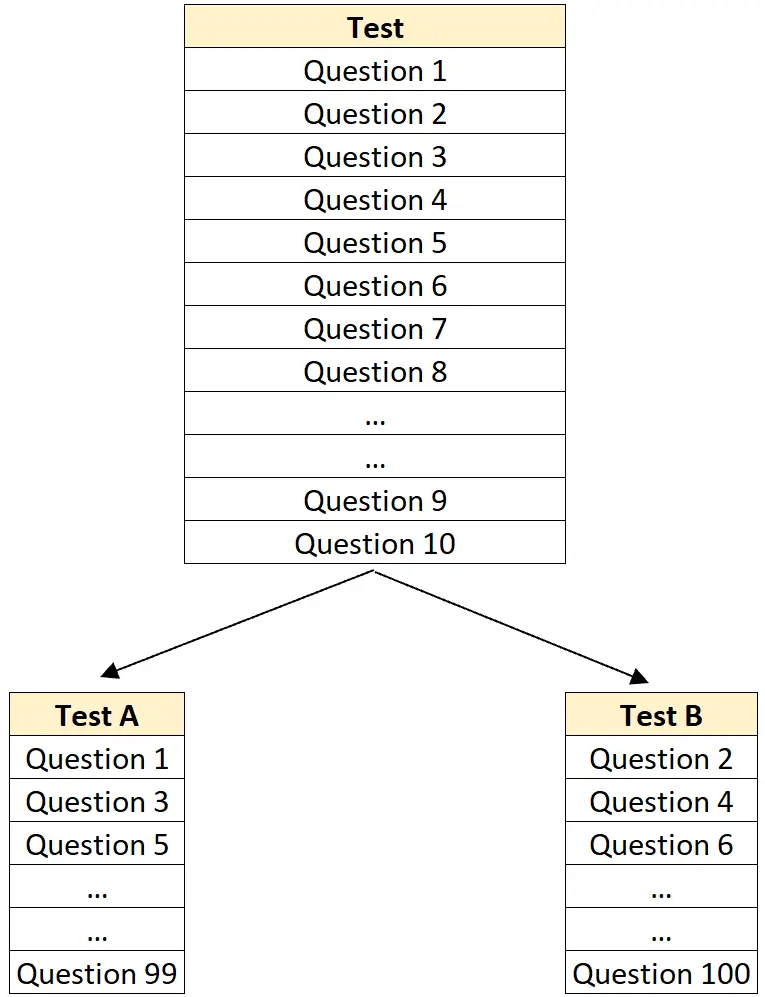
चरण 1: एक परीक्षण को आधे में विभाजित करें।

उदाहरण के लिए, 100-प्रश्न वाले परीक्षण को बेतरतीब ढंग से एक परीक्षण ए में विभाजित करें जिसमें 50 प्रश्न हों और एक परीक्षण बी में भी 50 प्रश्न हों।

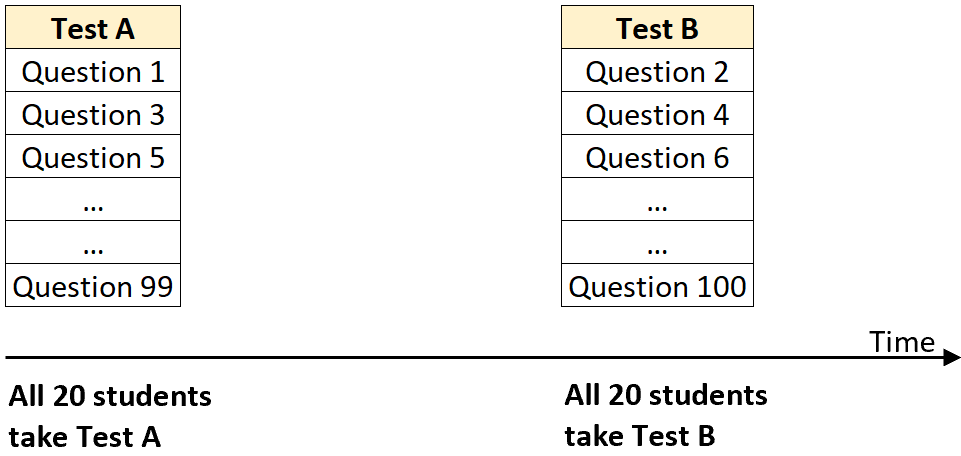
चरण 2: पहले भाग को सभी विद्यार्थियों को प्रशासित करें, फिर दूसरे भाग को सभी विद्यार्थियों को प्रशासित करें।

उदाहरण के लिए, एक निश्चित कक्षा के सभी 20 छात्रों को टेस्ट ए दें और उनके अंक रिकॉर्ड करें। फिर, शायद एक महीने बाद, उन्हीं 20 छात्रों को टेस्ट बी दें और उस टेस्ट में उनके अंक भी दर्ज करें।

चरण 3: दो परीक्षणों के परीक्षण अंकों के बीच सहसंबंध की गणना करें।

दोनों परीक्षणों के अंकों के बीच सहसंबंध की गणना करें। यदि अंकों के बीच सह-संबंध अधिक है तो एक परीक्षण को समानांतर रूप की विश्वसनीयता कहा जाता है।

समानांतर रूपों की विश्वसनीयता का उपयोग कब करें

समानांतर रूप विश्वसनीयता का उपयोग अक्सर अकादमिक सेटिंग्स में किया जाता है जब कोई प्रोफेसर नहीं चाहता कि छात्रों को पहले से ही परीक्षण प्रश्नों तक पहुंच प्राप्त हो।

उदाहरण के लिए, यदि प्रोफेसर सेमेस्टर की शुरुआत में सभी छात्रों को टेस्ट ए वितरित करता है, और फिर सेमेस्टर के अंत में उसी टेस्ट ए को वितरित करता है, तो छात्र पहले टेस्ट के प्रश्नों और उत्तरों को आसानी से याद कर सकते हैं।

हालाँकि, सेमेस्टर के अंत में एक अलग बी परीक्षा देकर (और उम्मीद है कि समान कठिनाई होगी), प्रोफेसर यह सुनिश्चित करते हुए छात्रों के ज्ञान का आकलन करने में सक्षम है कि छात्रों ने पहले प्रश्न नहीं देखे हैं।

समानांतर प्रपत्र विश्वसनीयता के संभावित नुकसान

समानांतर रूपों की विश्वसनीयता के दो संभावित नुकसान हैं:

1. इसमें बहुत सारे प्रश्नों की आवश्यकता होती है।

समानांतर रूपों की विश्वसनीयता बड़ी संख्या में प्रश्नों (उदाहरण के लिए 100 प्रश्न) वाले परीक्षणों के लिए सबसे अच्छा काम करती है, क्योंकि सहसंबंध के लिए हम जिस संख्या की गणना करेंगे वह अधिक विश्वसनीय होगी।

2. इस बात की कोई गारंटी नहीं है कि दोनों हिस्से वास्तव में समानांतर हैं।

जब हम किसी परीक्षण को बेतरतीब ढंग से दो हिस्सों में विभाजित करते हैं, तो इस बात की कोई गारंटी नहीं है कि कठिनाई में दोनों हिस्से वास्तव में समानांतर या “बराबर” होंगे। इसका मतलब यह है कि दो परीक्षणों के बीच स्कोर केवल इसलिए भिन्न हो सकते हैं क्योंकि एक आधा दूसरे की तुलना में अधिक कठिन साबित होता है।

समानांतर रूप विश्वसनीयता और विभाजित-आधा विश्वसनीयता

समानांतर रूपों की विश्वसनीयता आधी विश्वसनीयता के समान है, लेकिन इसमें थोड़ा अंतर है:

विश्वसनीयता दो भागों में विभाजित:

इसमें एक परीक्षा को दो हिस्सों में विभाजित करना और प्रत्येक आधे को छात्रों के एक ही समूह को प्रशासित करना शामिल है। छात्र किस क्रम में परीक्षा देते हैं, इससे कोई फर्क नहीं पड़ता।

इस पद्धति का लाभ आंतरिक स्थिरता को मापना है। आदर्श रूप से, हम चाहेंगे कि हिस्सों के बीच सहसंबंध उच्च हो, क्योंकि यह इंगित करता है कि परीक्षण के सभी हिस्से जो मापा जा रहा है उसमें समान रूप से योगदान करते हैं।

समानांतर रूपों की विश्वसनीयता:

इसमें एक परीक्षा को दो हिस्सों में विभाजित करना – उन्हें “ए” और “बी” कहना – और प्रत्येक आधे को छात्रों के एक ही समूह को प्रशासित करना शामिल है।

हालाँकि, यह महत्वपूर्ण है कि सभी छात्र पहले “ए” परीक्षा दें, फिर “बी” परीक्षा दें, ताकि “ए” परीक्षा के उत्तर जानने से बाद में “ए” परीक्षा देने वाले छात्रों को कोई लाभ न मिले। बी”।

अतिरिक्त संसाधन

विश्वसनीयता विश्लेषण का एक त्वरित परिचय
विश्वसनीयता को आधे में विभाजित करना क्या है?
परीक्षण-पुनः परीक्षण विश्वसनीयता क्या है?
अंतर-रेटर विश्वसनीयता क्या है?