समूहीकृत डेटा के लिए चतुर्थक की गणना कैसे करें
चतुर्थक वे मान हैं जो डेटा सेट को चार बराबर भागों में विभाजित करते हैं।
समूहीकृत डेटा के लिए चतुर्थक की गणना करने के लिए आप निम्न सूत्र का उपयोग कर सकते हैं:
क्यू आई = एल + (सी/एफ) * (आईएन/4 – एम)
सोना:
- एल : अंतराल की निचली सीमा जिसमें i वें चतुर्थक शामिल है
- सी : कक्षा की चौड़ाई
- एफ : अंतराल की आवृत्ति जिसमें i वें चतुर्थक शामिल है
- एन : कुल आवृत्ति
- एम : उस अंतराल की ओर ले जाने वाली संचयी आवृत्ति जिसमें i वें चतुर्थक शामिल है
निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें।
उदाहरण: समूहीकृत डेटा के लिए चतुर्थक की गणना करें
मान लीजिए हमारे पास निम्नलिखित आवृत्ति वितरण है:
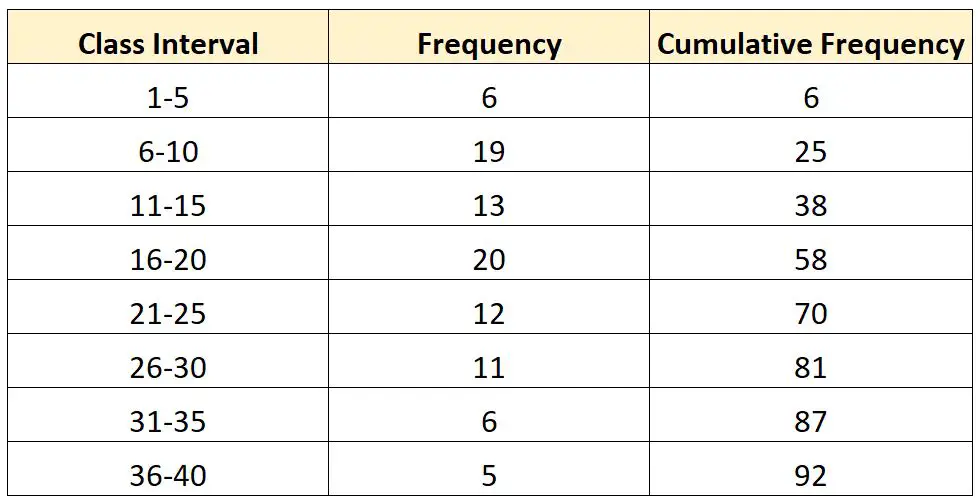
अब मान लीजिए कि हम इस वितरण के तीसरे चतुर्थक (क्यू 3 ) पर मूल्य की गणना करना चाहते हैं।
तीसरे चतुर्थक का मान वितरण में स्थिति (iN/4) पर स्थित होगा।
तो, (iN/4) = (3*92/4) = 69.
जिस अंतराल में तीसरा चतुर्थक शामिल है वह अंतराल 21-25 होगा क्योंकि 69, 58 और 70 की संचयी आवृत्तियों के बीच स्थित है।
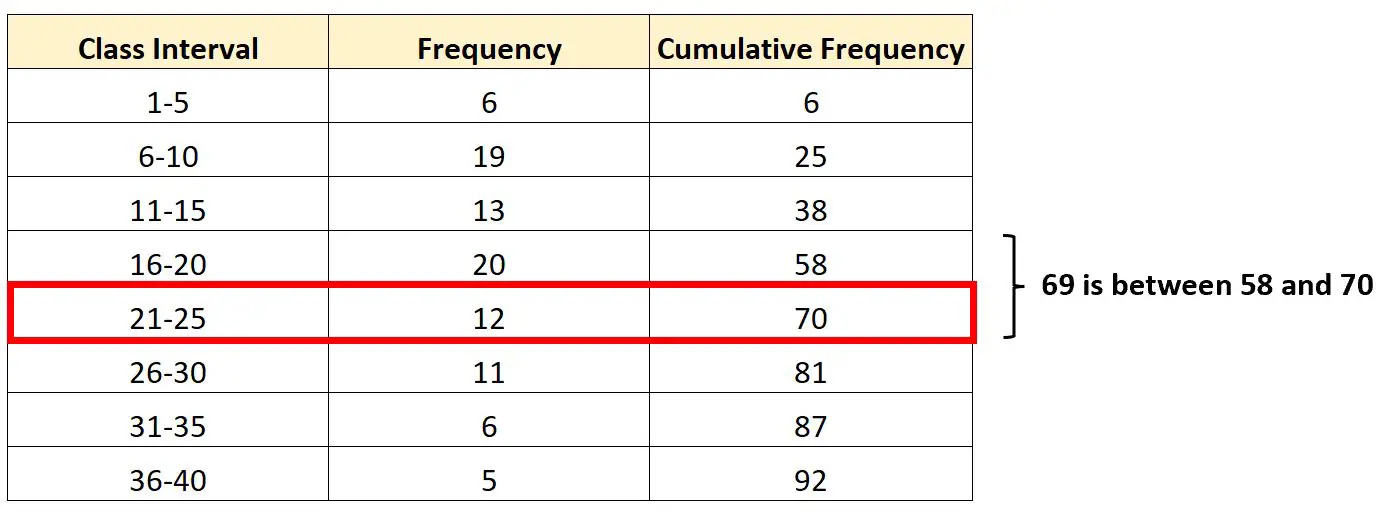
यह जानकर, हम अपने सूत्र में प्लग करने के लिए प्रत्येक आवश्यक मान पा सकते हैं:
एल : अंतराल की निचली सीमा जिसमें i वें चतुर्थक शामिल है
- अंतराल की निचली सीमा 21 है।
सी : कक्षा की चौड़ाई
- वर्ग की चौड़ाई की गणना इस प्रकार की जाती है: 25 – 21 = 4 ।
एफ : अंतराल की आवृत्ति जिसमें i वें चतुर्थक शामिल है
- कक्षा 21-25 की आवृत्ति 12 है
एन : कुल आवृत्ति
- तालिका में कुल संचयी आवृत्ति 92 है।
एम : उस अंतराल की ओर ले जाने वाली संचयी आवृत्ति जिसमें i वें चतुर्थक शामिल है
- कक्षा 21-25 तक संचयी आवृत्ति 58 है।
फिर हम तीसरे चतुर्थक पर मान ज्ञात करने के लिए इन सभी मानों को पिछले सूत्र में प्लग कर सकते हैं:
- क्यू आई = एल + (सी/एफ) * (आईएन/4 – एम)
- क्यू 3 = 21 + (4/12) * ((3)(92)/4 – 58)
- Q3 = 24.67
तीसरे चतुर्थक का मान 24.67 है।
आप पहले और दूसरे चतुर्थक मानों की गणना के लिए एक समान दृष्टिकोण का उपयोग कर सकते हैं।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल समूहीकृत डेटा के साथ काम करने के बारे में अतिरिक्त जानकारी प्रदान करते हैं:
समूहीकृत डेटा का माध्य और मानक विचलन कैसे ज्ञात करें
समूहीकृत डेटा मोड कैसे खोजें
समूहीकृत डेटा का माध्यिका कैसे ज्ञात करें
समूहीकृत या असमूहीकृत आवृत्ति वितरण