सरल रेखीय प्रतिगमन

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 2, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में सरल रैखिक प्रतिगमन क्या है और यह कैसे किया जाता है। इसी तरह, आपको एक सरल रैखिक प्रतिगमन अभ्यास हल किया हुआ मिलेगा और, इसके अलावा, एक सरल रैखिक प्रतिगमन कैलकुलेटर भी ऑनलाइन मिलेगा।

सरल रेखीय प्रतिगमन क्या है?

सरल रेखीय प्रतिगमन एक सांख्यिकीय मॉडल है जिसका उपयोग एक स्वतंत्र चर से संबंधित करने के लिए किया जाता है और हम दो चर के बीच क्या संबंध है, इसका अनुमान लगाने का प्रयास करते हैं।

इसलिए, सरल रैखिक प्रतिगमन का उपयोग ऐसे समीकरण को खोजने के लिए किया जाता है जो दो चर को रैखिक रूप से जोड़ता है। तार्किक रूप से, दो चर के बीच संबंध रैखिक होना चाहिए, अन्यथा किसी अन्य प्रकार के प्रतिगमन मॉडल का उपयोग किया जाना चाहिए।

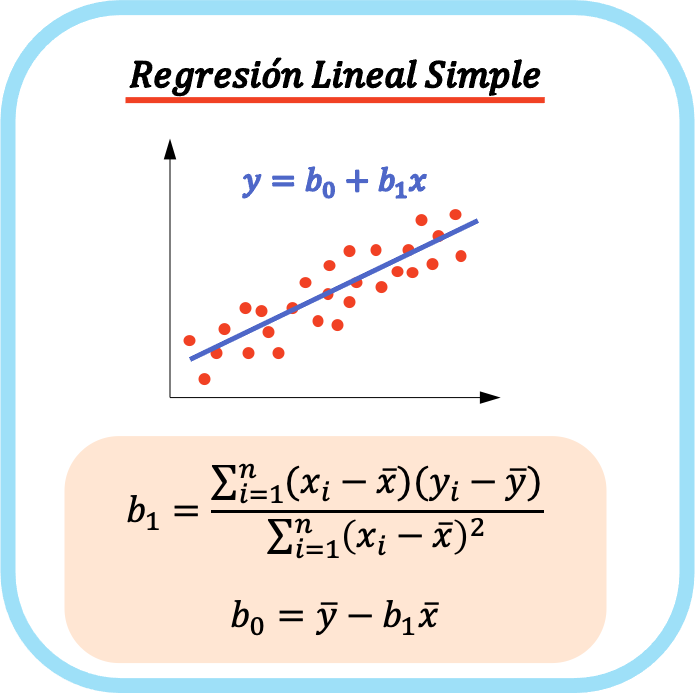
एक सरल रेखीय प्रतिगमन मॉडल का समीकरण दो गुणांकों से बना है: समीकरण का स्थिरांक (बी ₀ ) और दो चर के बीच सहसंबंध गुणांक (बी ₁ )। इसलिए, एक सरल रैखिक प्रतिगमन मॉडल के लिए समीकरण y=b ₀ +b ₁ x है।

$y=b_0+b_1x$

एक साधारण रेखीय प्रतिगमन के समीकरण को एक सीधी रेखा के रूप में रेखांकन किया जाता है, इसलिए गुणांक b ₀ अंतःखंड है और गुणांक b ₁ रेखा का ढलान है।

सरल रैखिक प्रतिगमन सूत्र

सरल रेखीय प्रतिगमन के गुणांकों की गणना के सूत्र इस प्रकार हैं:

👉 आप किसी भी डेटा सेट के लिए सरल रैखिक प्रतिगमन के गुणांक की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

जाहिर है, सरल रैखिक प्रतिगमन मॉडल से उत्पन्न समीकरण सभी अवलोकनों के सटीक मूल्य का अनुमान लगाने में सक्षम नहीं होगा, क्योंकि यह मॉडल केवल एक समीकरण खोजने का प्रयास करता है जो दो चर के बीच संबंध का अनुमान लगाता है। इस प्रकार, अवशिष्ट को वास्तविक मूल्य और रैखिक प्रतिगमन मॉडल द्वारा अनुमानित मूल्य के बीच अंतर के रूप में परिभाषित किया गया है।

$e_i=y_i-\widehat{y}_i$

ध्यान दें कि एक सरल रैखिक प्रतिगमन मॉडल का लक्ष्य अवशेषों के वर्गों को न्यूनतम करना है, अर्थात, सरल रैखिक प्रतिगमन न्यूनतम वर्ग मानदंड पर आधारित है।

एक सरल रेखीय प्रतिगमन का ठोस उदाहरण

सरल रैखिक प्रतिगमन विधि को समझने के लिए, यहां एक व्यावहारिक चरण-दर-चरण उदाहरण दिया गया है जिसमें एक सरल रैखिक प्रतिगमन मॉडल के समीकरण की गणना सांख्यिकीय डेटा के एक सेट से की जाती है।

सांख्यिकी परीक्षा देने के बाद, पांच छात्रों से पूछा गया कि उन्होंने परीक्षा के लिए कितने घंटे का अध्ययन समर्पित किया है। डेटा नीचे दी गई तालिका में प्रस्तुत किया गया है। अध्ययन के घंटों को प्राप्त ग्रेड से रैखिक रूप से जोड़ने के लिए एकत्रित सांख्यिकीय डेटा का एक सरल रैखिक प्रतिगमन मॉडल निष्पादित करें।

एक सरल रेखीय प्रतिगमन मॉडल को पूरा करने के लिए हमें समीकरण के गुणांक बी ₀ और बी ₁ निर्धारित करना होगा और इसके लिए, हमें उपरोक्त अनुभाग में देखे गए सूत्रों का उपयोग करना होगा।

हालाँकि, सरल रैखिक प्रतिगमन सूत्रों को लागू करने के लिए, हमें पहले स्वतंत्र चर के माध्य और आश्रित चर के माध्य की गणना करनी होगी:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

अब जब हम चरों के माध्य जानते हैं, तो हम मॉडल के गुणांक b ₁ की गणना उसके संगत सूत्र का उपयोग करके करते हैं:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

अंत में, हम संबंधित सूत्र का उपयोग करके मॉडल के गुणांक b ₀ की गणना करते हैं:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

संक्षेप में, समस्या के सरल रैखिक प्रतिगमन मॉडल के लिए समीकरण है:

$y=2,0294+0,4412x$

नीचे आप नमूना डेटा के चित्रमय प्रतिनिधित्व के साथ-साथ सरल रैखिक प्रतिगमन मॉडल की सीधी रेखा देख सकते हैं:

अंत में, एक बार जब हमने सरल रैखिक प्रतिगमन मॉडल के समीकरण की गणना कर ली है, तो जो कुछ बचा है वह प्राप्त परिणाम की व्याख्या करना है। इसके लिए, प्रतिगमन मॉडल के निर्धारण के गुणांक की गणना करना आवश्यक है, आप हमारी वेबसाइट पर संबंधित लेख की खोज करके देख सकते हैं कि यह कैसे किया जाता है।

सरल रेखीय प्रतिगमन धारणाएँ

एक सरल रेखीय प्रतिगमन करने के लिए, निम्नलिखित मान्यताओं को पूरा किया जाना चाहिए:

स्वतंत्रता : देखे गए अवशेष एक दूसरे से स्वतंत्र होने चाहिए। मॉडल की स्वतंत्रता सुनिश्चित करने का एक सामान्य तरीका नमूनाकरण प्रक्रिया में यादृच्छिकता जोड़ना है।
समरूपता : अवशेषों की भिन्नता में एकरूपता होनी चाहिए, अर्थात अवशेषों की परिवर्तनशीलता स्थिर होनी चाहिए।
सामान्यता : अवशेषों को सामान्य रूप से वितरित किया जाना चाहिए, या दूसरे शब्दों में, उन्हें माध्य 0 के साथ सामान्य वितरण का पालन करना चाहिए।
रैखिकता – स्वतंत्र चर और आश्रित चर के बीच संबंध रैखिक होना चाहिए।

सरल रेखीय प्रतिगमन कैलक्यूलेटर

दो चरों के बीच एक सरल रैखिक प्रतिगमन मॉडल फिट करने के लिए नीचे दिए गए कैलकुलेटर में एक नमूना डेटा प्लग करें। आपको डेटा जोड़े को अलग करने की आवश्यकता है, ताकि पहले बॉक्स में केवल स्वतंत्र चर X के मान हों और दूसरे बॉक्स में केवल आश्रित चर Y के मान हों।

डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

सरल और एकाधिक रैखिक प्रतिगमन

अंत में, हम देखेंगे कि सरल रैखिक प्रतिगमन और एकाधिक रैखिक प्रतिगमन के बीच क्या अंतर है, क्योंकि वे दो प्रकार के रैखिक प्रतिगमन हैं जो अक्सर आंकड़ों में उपयोग किए जाते हैं।

एकाधिक रेखीय प्रतिगमन गणितीय रूप से दो या दो से अधिक व्याख्यात्मक चर को एक प्रतिक्रिया चर से जोड़ना संभव बनाता है। अर्थात्, एकाधिक रेखीय प्रतिगमन में, एक मॉडल बनाया जाता है जिसमें कम से कम दो स्वतंत्र चर होते हैं।

इसलिए, सरल रैखिक प्रतिगमन और एकाधिक रैखिक प्रतिगमन के बीच का अंतर स्वतंत्र चर की संख्या है। सरल रैखिक प्रतिगमन में, केवल एक स्वतंत्र चर होता है, जबकि एकाधिक रैखिक प्रतिगमन में, दो या अधिक स्वतंत्र चर होते हैं।

➤ देखें: एकाधिक रैखिक प्रतिगमन

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने