आपको सहसंबंध का उपयोग कब करना चाहिए? (स्पष्टीकरण एवं उदाहरण)

सहसंबंध का उपयोग दो चरों के बीच रैखिक संबंध को मापने के लिए किया जाता है।

सहसंबंध गुणांक हमेशा -1 और 1 के बीच मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

छात्र अक्सर एक प्रश्न पूछते हैं: मुझे सहसंबंध का उपयोग कब करना चाहिए?

संक्षिप्त उत्तर: जब आप दो चरों के बीच रैखिक संबंध को मापना चाहते हैं तो सहसंबंध का उपयोग करें और कोई भी चर किसी प्रतिक्रिया या “परिणाम” चर का प्रतिनिधित्व नहीं करता है।

निम्नलिखित उदाहरण बताते हैं कि आपको व्यवहार में सहसंबंध का उपयोग कब करना चाहिए और कब नहीं करना चाहिए।

उदाहरण 1: सहसंबंध का उपयोग कब करें

मान लीजिए कि एक प्रोफेसर अपनी कक्षा में छात्रों के गणित परीक्षण के अंकों और विज्ञान परीक्षण के अंकों के बीच रैखिक संबंध को समझना चाहता है।

उदाहरण के लिए, क्या गणित की परीक्षा में अच्छा प्रदर्शन करने वाले छात्र विज्ञान की परीक्षा में भी अच्छा प्रदर्शन करते हैं? या क्या जो छात्र गणित में उच्च अंक प्राप्त करते हैं, वे विज्ञान में कम अंक प्राप्त करते हैं?

इस परिदृश्य में, वह गणित परीक्षा के अंकों और विज्ञान परीक्षा के अंकों के बीच सहसंबंध की गणना कर सकता है क्योंकि वह केवल दो चर के बीच रैखिक संबंध को समझना चाहता है और किसी भी चर को प्रतिक्रिया चर नहीं माना जा सकता है।

मान लीजिए कि वह पियर्सन सहसंबंध गुणांक की गणना करता है और पाता है कि यह r = 0.78 है। यह एक मजबूत सकारात्मक सहसंबंध है, जिसका अर्थ है कि जो छात्र गणित में अच्छा प्रदर्शन करते हैं वे विज्ञान में भी अच्छा प्रदर्शन करते हैं।

उदाहरण 2: सहसंबंध का उपयोग कब नहीं करना चाहिए

मान लीजिए कि किसी कंपनी का विपणन विभाग कुल राजस्व पर विज्ञापन खर्च के प्रभाव की मात्रा निर्धारित करना चाहता है।

उदाहरण के लिए, विज्ञापन पर खर्च किए गए प्रत्येक अतिरिक्त डॉलर के लिए, कंपनी कितना अतिरिक्त राजस्व अर्जित करने की उम्मीद कर सकती है?

इस परिदृश्य में, विभाग को विज्ञापन खर्च और कुल राजस्व के बीच संबंध को मापने के लिए एक रैखिक प्रतिगमन मॉडल का उपयोग करना चाहिए, क्योंकि “राजस्व” चर प्रतिक्रिया चर है।

मान लीजिए कि विभाग एक सरल रेखीय प्रतिगमन मॉडल लागू करता है और पाता है कि निम्नलिखित समीकरण विज्ञापन खर्च और कुल राजस्व के बीच संबंध का सबसे अच्छा वर्णन करता है:

कुल राजस्व = 145.4 + 0.34*(विज्ञापन व्यय)

हम इसका मतलब यह निकालेंगे कि विज्ञापन पर खर्च किए गए प्रत्येक अतिरिक्त डॉलर के परिणामस्वरूप कुल राजस्व में औसतन $0.34 की वृद्धि होती है।

सहसंबंध का उपयोग करने के लिए सावधानियां

यह ध्यान रखना महत्वपूर्ण है कि सहसंबंध का उपयोग केवल दो चर के बीच रैखिक संबंध को मापने के लिए किया जा सकता है।

हालाँकि, कुछ परिस्थितियों में, एक सहसंबंध गुणांक एक गैर-रेखीय संबंध साझा करने वाले दो चर के बीच संबंध को प्रभावी ढंग से पकड़ने में सक्षम नहीं होगा।

उदाहरण के लिए, मान लीजिए कि हम दो चरों के बीच संबंध को देखने के लिए निम्नलिखित स्कैटरप्लॉट बनाते हैं:

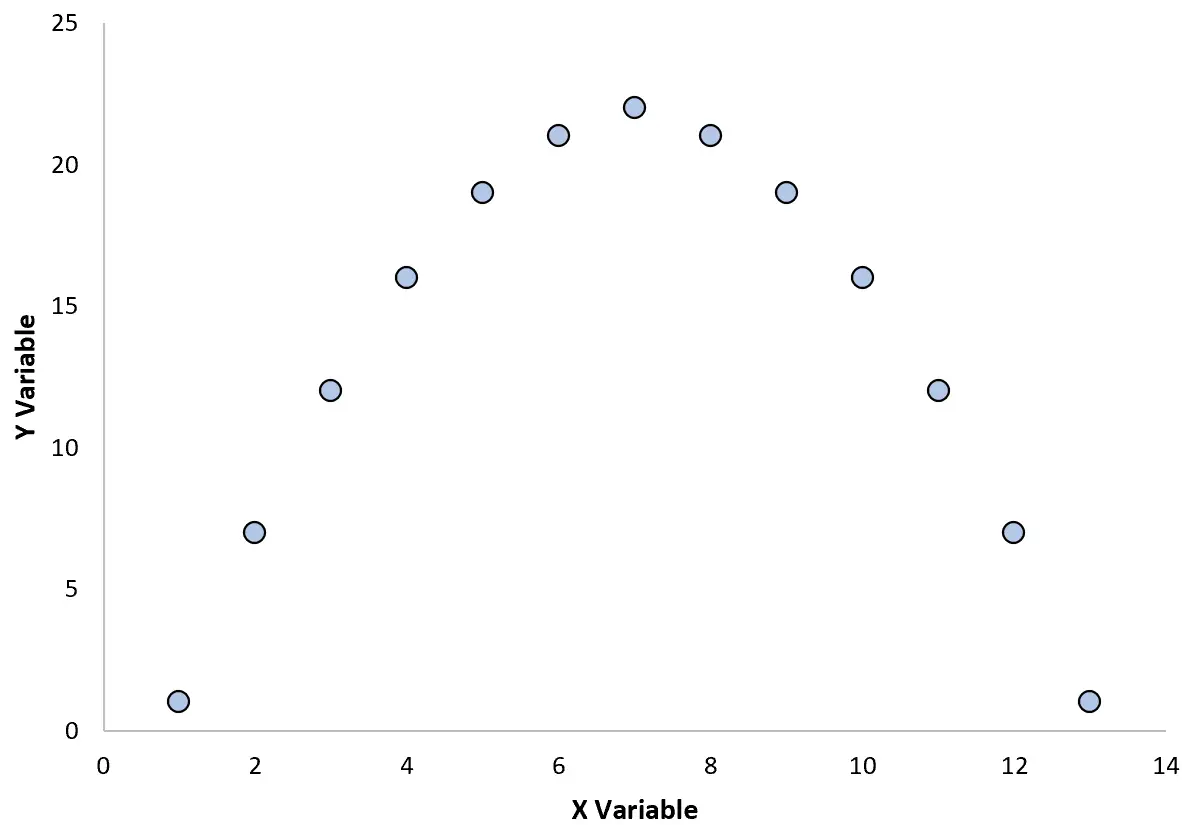
यदि हम इन दो चरों के बीच सहसंबंध गुणांक की गणना करते हैं, तो यह r = 0 निकलता है। इसका मतलब है कि दोनों चरों के बीच कोई रैखिक संबंध नहीं है।

हालाँकि, ग्राफ़ से हम देख सकते हैं कि दोनों चरों में वास्तव में एक संबंध है – यह एक रैखिक संबंध के बजाय बस एक द्विघात संबंध है।

इसलिए, दो चरों के बीच सहसंबंध की गणना करते समय, ध्यान रखें कि चरों के बीच संबंध की कल्पना करने के लिए एक स्कैटरप्लॉट बनाना भी उपयोगी हो सकता है।

भले ही दो चरों में एक रैखिक संबंध न हो, यह संभव है कि उनमें एक गैर-रेखीय संबंध हो जो एक स्कैटरप्लॉट में प्रकट होगा।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल अधिक विस्तार से बताते हैं कि विभिन्न परिस्थितियों में सहसंबंध का उपयोग कैसे किया जाता है:

सहसंबंध के 6 वास्तविक जीवन के उदाहरण
“मजबूत” सहसंबंध क्या माना जाता है?
सहसंबंध बनाम एसोसिएशन: क्या अंतर है?
सहसंबंध बनाम प्रतिगमन: क्या अंतर है?