सहसंबंध बनाम प्रतिगमन: क्या अंतर है?

सहसंबंध और प्रतिगमन दो संबंधित, लेकिन पूरी तरह से समान नहीं, सांख्यिकीय शब्द हैं।

इस ट्यूटोरियल में, हम दोनों शब्दों का संक्षिप्त विवरण प्रदान करेंगे और बताएंगे कि वे कैसे समान और भिन्न हैं।

सहसंबंध क्या है?

सहसंबंध दो चर, x और y के बीच रैखिक संबंध को मापता है। इसका मान -1 और 1 के बीच है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित डेटा सेट है जिसमें दो चर हैं: (1) अध्ययन के घंटे और (2) 20 अलग-अलग छात्रों के लिए प्राप्त परीक्षा अंक:

यदि हमने अध्ययन किए गए घंटों बनाम परीक्षा परिणामों का एक स्कैटरप्लॉट बनाया, तो यह इस तरह दिखेगा:

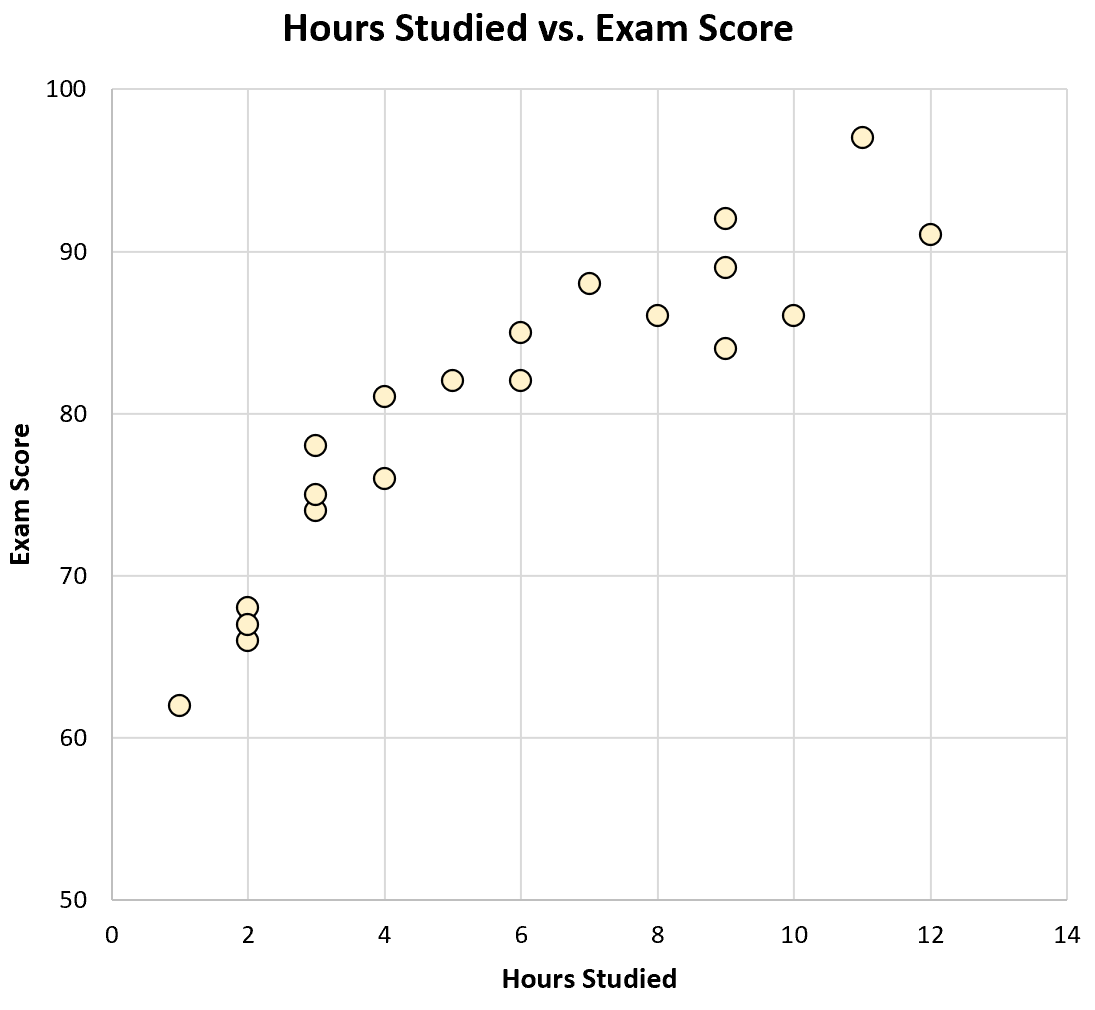
ग्राफ़ को देखकर ही हम देख सकते हैं कि जो छात्र अधिक पढ़ाई करते हैं वे परीक्षा में बेहतर प्रदर्शन करते हैं। दूसरे शब्दों में, हम स्पष्ट रूप से देख सकते हैं कि दोनों चरों के बीच एक सकारात्मक सहसंबंध है।

कैलकुलेटर का उपयोग करके, हम देख सकते हैं कि इन दो चरों के बीच सहसंबंध r = 0.915 है। यह मान 1 के करीब है, यह पुष्टि करता है कि दो चर के बीच एक मजबूत सकारात्मक सहसंबंध है।

प्रतिगमन क्या है?

प्रतिगमन एक ऐसी विधि है जिसका उपयोग हम यह समझने के लिए कर सकते हैं कि वेरिएबल x के मानों को बदलने से वेरिएबल y के मानों पर क्या प्रभाव पड़ता है।

एक प्रतिगमन मॉडल एक चर, x को भविष्यवक्ता चर के रूप में और दूसरे चर, y , को प्रतिक्रिया चर के रूप में उपयोग करता है। इसके बाद यह निम्नलिखित रूप का एक समीकरण ढूंढता है जो दो चरों के बीच संबंध का सबसे अच्छा वर्णन करता है:

ŷ = बी ₀ + बी ₁ एक्स

सोना:

• ŷ: प्रतिक्रिया चर का अनुमानित मूल्य
• b ₀ : मूल बिंदु पर कोटि (y का मान जब x शून्य के बराबर हो)
• बी ₁ : प्रतिगमन गुणांक (x में एक इकाई वृद्धि के लिए y में औसत वृद्धि)
• x: पूर्वानुमानित चर का मान

उदाहरण के लिए, हमारे पिछले डेटासेट पर विचार करें:

एक रेखीय प्रतिगमन कैलकुलेटर का उपयोग करके, हम पाते हैं कि निम्नलिखित समीकरण इन दो चर के बीच संबंध का सबसे अच्छा वर्णन करता है:

अनुमानित परीक्षा स्कोर = 65.47 + 2.58*(अध्ययन के घंटे)

इस समीकरण की व्याख्या करने का तरीका यह है:

• शून्य घंटे पढ़ने वाले छात्र के लिए अनुमानित परीक्षा स्कोर 65.47 है।
• अध्ययन के एक अतिरिक्त घंटे से जुड़ी औसत परीक्षा स्कोर वृद्धि 2.58 है।

हम इस समीकरण का उपयोग यह अनुमान लगाने के लिए भी कर सकते हैं कि अध्ययन किए गए घंटों की संख्या के आधार पर एक छात्र को कितना स्कोर मिलेगा।

उदाहरण के लिए, एक छात्र जो 6 घंटे पढ़ाई करता है उसे 80.95 का ग्रेड प्राप्त होना चाहिए:

अनुमानित परीक्षा स्कोर = 65.47 + 2.58*(6) = 80.95 ।

हम इस समीकरण को स्कैटर प्लॉट पर एक रेखा के रूप में भी प्लॉट कर सकते हैं:

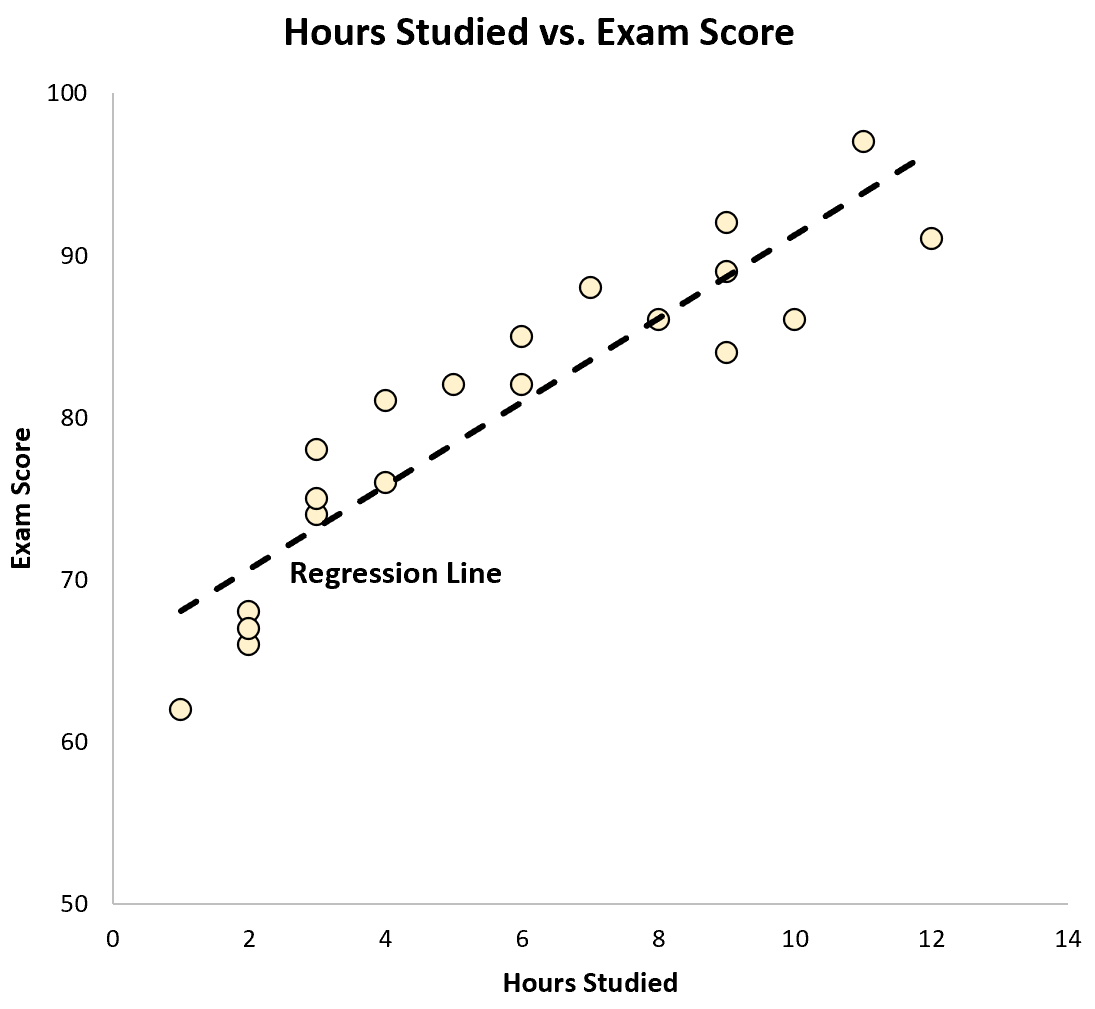
हम देख सकते हैं कि प्रतिगमन रेखा डेटा को काफी अच्छी तरह से “फिट” करती है।

पहले याद करें कि इन दोनों चरों के बीच सहसंबंध r = 0.915 था। यह पता चला है कि हम इस मान का वर्ग कर सकते हैं और “आर वर्ग” नामक एक संख्या प्राप्त कर सकते हैं जो प्रतिक्रिया चर में भिन्नता के कुल अनुपात का वर्णन करता है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

इस उदाहरण में, r ² = 0.915 ² = 0.837 । इसका मतलब यह है कि परीक्षा के अंकों में 83.7% भिन्नता को अध्ययन किए गए घंटों की संख्या से समझाया जा सकता है।

सहसंबंध बनाम प्रतिगमन: समानताएं और अंतर

यहां सहसंबंध और प्रतिगमन के बीच समानताएं और अंतर का सारांश दिया गया है:

समानताएँ:

• दोनों दो चरों के बीच संबंध की दिशा निर्धारित करते हैं।
• दोनों दो चरों के बीच संबंध की ताकत को मापते हैं।

मतभेद:

• प्रतिगमन दो चरों के बीच कारण और प्रभाव संबंध दिखाने में सक्षम है। सहसंबंध ऐसा नहीं करता.
• प्रतिगमन एक समीकरण का उपयोग करके दूसरे चर के मूल्य के आधार पर एक चर के मूल्य की भविष्यवाणी करने में सक्षम है। सहसंबंध ऐसा नहीं करता.
• प्रतिगमन दो चरों के बीच संबंध को मापने के लिए एक समीकरण का उपयोग करता है। सहसंबंध एकल संख्या का उपयोग करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल इस आलेख में शामिल विषयों की अधिक गहन व्याख्या प्रदान करते हैं।

पियर्सन सहसंबंध गुणांक का एक परिचय
सरल रेखीय प्रतिगमन का एक परिचय
सरल रेखीय प्रतिगमन कैलक्यूलेटर
एक अच्छा आर-वर्ग मान क्या है?