एसओसीएस: वितरण का वर्णन करने के लिए एक उपयोगी संक्षिप्त शब्द

आंकड़ों में, हम अक्सर यह समझना चाहते हैं कि डेटा का एक सेट कैसे वितरित किया जाता है। विशेष रूप से, चार चीजें हैं जो वितरण के बारे में जानने के लिए उपयोगी हैं:

1 . आकार

• क्या वितरण सममित है या एक तरफ झुका हुआ है?
• क्या वितरण एक-मोडल (एक शिखर) या द्वि-मोडल (दो शिखर) है?

2. आउटलाइर्स

• क्या वितरण में कोई आउटलेयर मौजूद हैं?

3. केंद्र

• माध्य, मध्यिका और वितरण का तरीका क्या है?

4.प्रसार

• वितरण की सीमा, अंतरचतुर्थक सीमा, मानक विचलन और विचरण क्या हैं?

एसओसीएस एक उपयोगी संक्षिप्त नाम है जिसका उपयोग हम इन चार चीजों को याद रखने के लिए कर सकते हैं। इसका अर्थ है “आकार, बाहरी हिस्से, केंद्र, फैलाव”।

आइए वितरण का वर्णन करने के लिए एसओसीएस का उपयोग कैसे करें इसका एक सरल उदाहरण देखें।

उदाहरण: वितरण का वर्णन करने के लिए एसओसीएस का उपयोग कैसे करें

मान लीजिए कि हमारे पास निम्नलिखित डेटा सेट है जो 20 विभिन्न पौधों के नमूने की ऊंचाई दर्शाता है।

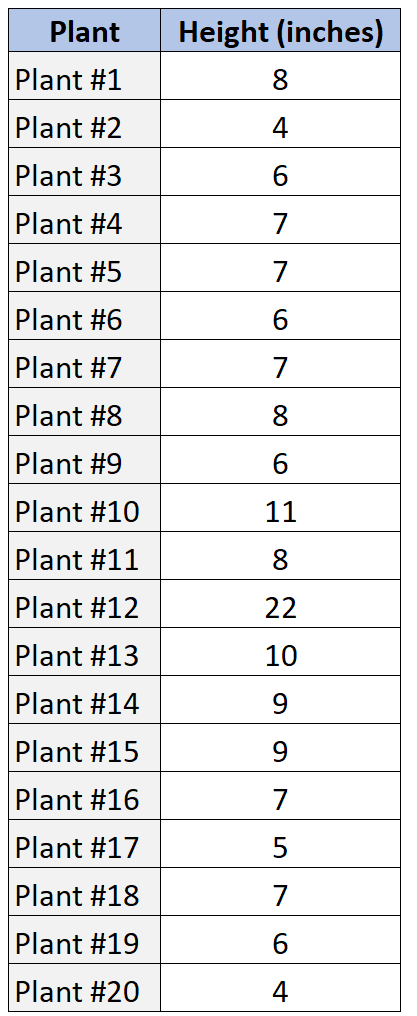
यहां बताया गया है कि हम डेटा मानों के इस वितरण का वर्णन करने के लिए एसओसीएस का उपयोग कैसे कर सकते हैं।

आकार

सबसे पहले, हम वितरण के आकार का वर्णन करना चाहते हैं।

वितरण के आकार की कल्पना करने का एक उपयोगी तरीका एक हिस्टोग्राम बनाना है, जो डेटा सेट में प्रत्येक मान की आवृत्तियों को प्रदर्शित करता है:

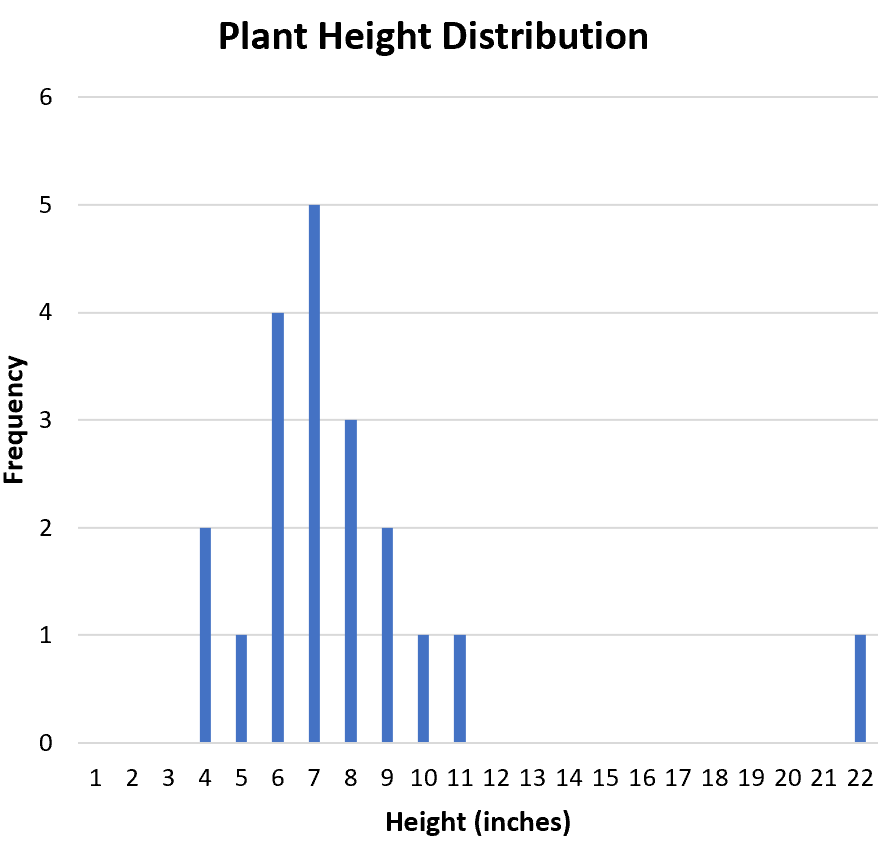
क्या वितरण सममित है या एक तरफ झुका हुआ है?   हिस्टोग्राम से हम देख सकते हैं कि वितरण लगभग सममित है। दूसरे शब्दों में, मूल्य एक या दूसरे तरीके से पक्षपाती नहीं हैं।

क्या वितरण एक-मोडल (एक शिखर) या द्वि-मोडल (दो शिखर) है? वितरण एकरूप है। इसका चरम मान “7” है।

बाहरी कारकों के कारण

इसके बाद, हम यह निर्धारित करना चाहते हैं कि डेटासेट में कोई आउटलेयर हैं या नहीं। हिस्टोग्राम से हम वितरण का निरीक्षण कर सकते हैं और देख सकते हैं कि 22 संभावित रूप से एक बाहरी है:

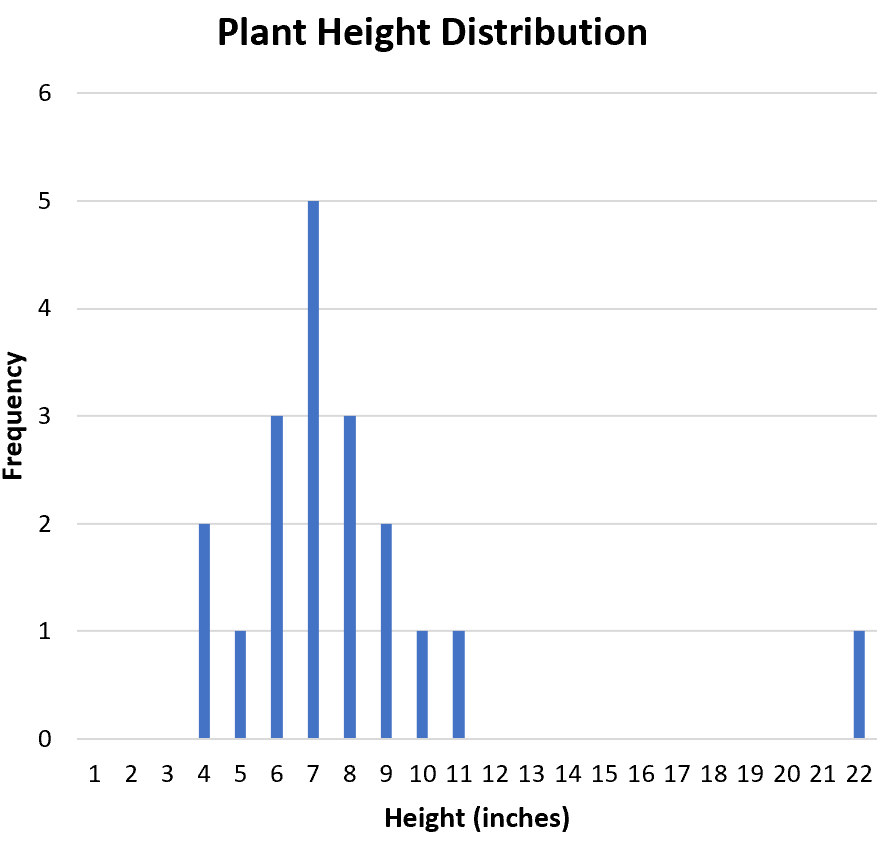
बाह्य को औपचारिक रूप से परिभाषित करने का एक सामान्य तरीका कोई भी मान है जो तीसरे चतुर्थक के ऊपर या पहले चतुर्थक के नीचे अंतरचतुर्थक सीमा का 1.5 गुना है।

इंटरक्वार्टाइल रेंज कैलकुलेटर का उपयोग करके, हम 20 कच्चे डेटा मान दर्ज कर सकते हैं और देख सकते हैं कि तीसरा चतुर्थक 9 है, इंटरक्वेर्टाइल रेंज 3 है, और इसलिए 9 + (1.5*3) = 13.5 से अधिक कोई भी मान एक बाहरी है, परिभाषा के अनुसार.

चूँकि 22, 13.5 से बड़ा है, हम 22 को बाह्य मान घोषित कर सकते हैं।

केंद्र

फिर हम यह वर्णन करना चाहते हैं कि वितरण का केंद्र कहाँ स्थित है। केंद्रीय प्रवृत्ति के तीन सामान्य माप जिनका हम उपयोग कर सकते हैं वे हैं माध्य, माध्यिका और बहुलक।

माध्य: यह वितरण का औसत मूल्य है। हम इसे सभी व्यक्तिगत मूल्यों को जोड़कर और फिर मूल्यों की कुल संख्या से विभाजित करके पाते हैं:

औसत = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85

माध्यिका: यह वितरण का “औसत” मान है। हम इसे सभी मानों को सबसे छोटे से सबसे बड़े तक क्रमबद्ध करके और फिर माध्य मान की पहचान करके पाते हैं। यह 7 निकला।

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

मोड: यह वह मान है जो सबसे अधिक बार दिखाई देता है। यह 7 निकला।

फैलाना

आगे, हम वितरण में मूल्यों के वितरण का वर्णन करना चाहते हैं। फैलाव के चार सामान्य उपाय जिनका हम उपयोग कर सकते हैं वे हैं रेंज, इंटरक्वेराइल रेंज, मानक विचलन और विचरण।

रेंज: यह डेटा सेट में सबसे बड़े और सबसे छोटे मान के बीच का अंतर है। यह 22 – 4 = 18 निकला।

इंटरक्वेर्टाइल रेंज: डेटा मानों के मध्य 50% की चौड़ाई को मापता है। इंटरक्वेर्टाइल रेंज कैलकुलेटर में 20 कच्चे डेटा मान दर्ज करके, हम देख सकते हैं कि यह 3 के बराबर है।

मानक विचलन: यह डेटा मानों के औसत वितरण का एक माप है। विचरण और मानक विचलन कैलकुलेटर में 20 कच्चे डेटा मान दर्ज करके, हम देख सकते हैं कि मानक विचलन 3.69 के बराबर है।

प्रसरण: यह केवल मानक विचलन है, वर्ग। यह 3.69 ² = 13.63 के बराबर है।

निष्कर्ष

एक गाइड के रूप में एसओसीएस का उपयोग करते हुए, हम पौधे की ऊंचाई वितरण का वर्णन इस प्रकार करने में सक्षम थे:

• वितरण एकरूप और सममित था, जिसका अर्थ है कि इसका केवल एक शिखर था और यह एक तरफ या दूसरे तरफ झुका हुआ नहीं था।
• वितरण में एक बाहरी हिस्सा था: 22।
• वितरण का माध्य 7.85, माध्यिका 7 और बहुलक 7 था।
• वितरण की सीमा 18, अंतरचतुर्थक सीमा 3, मानक विचलन 3.69 और विचरण 13.63 था।

ध्यान दें कि हम किसी भी वितरण का वर्णन करने के लिए एसओसीएस का उपयोग कर सकते हैं, जो हमारे लिए वितरण के आकार को पूरी तरह से समझने का एक उपयोगी तरीका है, चाहे इसमें आउटलेयर हों, लगभग केंद्र कहां है, और डेटा मानों को कैसे वितरित किया जाए। हैं।