आवृत्ति (सांख्यिकीय)

यह आलेख बताता है कि सांख्यिकी में आवृत्ति की अवधारणा क्या है। इस प्रकार, आप आँकड़ों में आवृत्ति की परिभाषा, मौजूद विभिन्न प्रकार की आवृत्तियाँ और अंत में, आवृत्ति तालिका कैसे बनाएं, पाएंगे।

सांख्यिकी में आवृत्ति क्या है?

आँकड़ों में, आवृत्ति किसी डेटा सेट में कोई मान प्रकट होने की संख्या है। सीधे शब्दों में कहें तो, आवृत्ति एक सांख्यिकीय नमूने में किसी मान को दोहराए जाने की संख्या है।

उदाहरण के लिए, यदि एक सर्वेक्षण में पांच लोगों ने उत्तर दिया कि उनका पसंदीदा रंग नीला है, तो नीले रंग की आवृत्ति 5 के बराबर है।

आम तौर पर, आंकड़ों में, सूचकांक i के साथ अक्षर f का उपयोग मान i की आवृत्ति को दर्शाने के लिए किया जाता है, इसलिए आवृत्ति का प्रतीक _fi है।

सभी आवृत्तियों का योग नमूने में डेटा की कुल संख्या देता है। इसलिए, किसी भी सांख्यिकीय अध्ययन के लिए निम्नलिखित सूत्र हमेशा मान्य होता है:

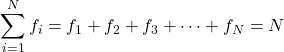
सोना

मान की आवृत्ति है

और

प्रेक्षणों की कुल संख्या है.

सांख्यिकी में आवृत्तियों के प्रकार

सांख्यिकी में, विभिन्न प्रकार की आवृत्तियाँ इस प्रकार हैं:

• पूर्ण आवृत्ति : सांख्यिकीय नमूने में कोई मान कितनी बार प्रकट होता है, उससे मेल खाती है।
• संचयी निरपेक्ष आवृत्ति : मान की पूर्ण आवृत्ति और सभी छोटे मानों की पूर्ण आवृत्तियों को जोड़कर गणना की जाती है।
• सापेक्ष आवृत्ति : यह डेटा की कुल संख्या से विभाजित पूर्ण आवृत्ति है।
• संचयी सापेक्ष आवृत्ति : मान की सापेक्ष आवृत्ति और सभी निचले मानों की सापेक्ष आवृत्तियों के योग के बराबर होती है।

नीचे दिए गए अनुभाग में आप देख सकते हैं कि प्रत्येक आवृत्ति प्रकार की गणना कैसे की जाती है।

आवृत्ति तालिका

आमतौर पर आंकड़ों में, डेटा के नमूने की आवृत्तियों की गणना को आवृत्ति तालिका में संक्षेपित किया जाता है। नीचे एक चरण-दर-चरण उदाहरण दिया गया है ताकि आप देख सकें कि यह कैसे करना है।

• 30 छात्रों की एक कक्षा में सांख्यिकी विषय में प्राप्त ग्रेड इस प्रकार हैं। डेटासेट की एक आवृत्ति तालिका बनाएं।

चूँकि सभी संख्याएँ केवल पूर्णांक हो सकती हैं, यह एक असतत चर है। इसलिए डेटा को अंतरालों में समूहित करना आवश्यक नहीं है।

इसलिए हमें एक तालिका बनाने की आवश्यकता है जिसमें प्रत्येक भिन्न मान एक पंक्ति होगी। इसके अलावा, हमें प्रत्येक मान की पूर्ण आवृत्ति ज्ञात करने की आवश्यकता है, ऐसा करने के लिए, बस डेटा नमूने में मान प्रकट होने की संख्या की गणना करें।

ध्यान दें कि सभी निरपेक्ष आवृत्तियों का योग डेटा की कुल संख्या के बराबर है। यदि इस नियम का सम्मान नहीं किया जाता है, तो इसका मतलब है कि आप कुछ जानकारी प्रदान करना भूल गए हैं।

अब जब हम निरपेक्ष आवृत्ति जानते हैं, तो हमें संचयी निरपेक्ष आवृत्ति ज्ञात करने की आवश्यकता है। इस गणना के लिए हमारे पास दो विकल्प हैं: या तो हम मूल्य की पूर्ण आवृत्ति और सबसे छोटे मूल्यों की सभी पूर्ण आवृत्तियों को जोड़ दें, या इसके विपरीत, हम मूल्य की पूर्ण आवृत्ति और पिछले मूल्य की संचयी पूर्ण आवृत्ति को जोड़ दें।

अंतिम मान की संचयी निरपेक्ष आवृत्ति हमेशा डेटा की कुल संख्या से मेल खाती है, आप यह सत्यापित करने के लिए इस ट्रिक का उपयोग कर सकते हैं कि गणना सही है।

इसके बाद, हमें सापेक्ष आवृत्ति निर्धारित करने की आवश्यकता है, जिसकी गणना पूर्ण आवृत्ति को डेटा बिंदुओं की कुल संख्या (30) से विभाजित करके की जाती है:

ध्यान रखें कि सभी सापेक्ष आवृत्तियों का योग हमेशा 1 के बराबर होता है, अन्यथा इसका मतलब है कि आवृत्ति तालिका में कुछ गणनाएँ गलत हैं।

अंततः, यह संचित सापेक्ष आवृत्ति को निकालने के लिए पर्याप्त है। ऐसा करने के लिए, आपको प्रश्न में मूल्य की सापेक्ष आवृत्ति और पिछली सभी सापेक्ष आवृत्तियों को जोड़ना होगा या, जो एक ही चीज़ के बराबर है, पिछली संचित सापेक्ष आवृत्ति:

संक्षेप में, समस्याग्रस्त डेटा की सभी आवृत्तियों के साथ आवृत्ति तालिका इस प्रकार है: