फ़ैशन (सांख्यिकी)

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में मोड क्या है। आप सीखेंगे कि समूहीकृत डेटा और असमूहीकृत डेटा के लिए सांख्यिकीय मोड, विभिन्न प्रकार के मोड और इस सांख्यिकीय माप के कई उदाहरण कैसे खोजें।

सांख्यिकी में मोड क्या है?

आंकड़ों में, मोड डेटा सेट में वह मान है जिसकी निरपेक्ष आवृत्ति सबसे अधिक है, अर्थात, मोड डेटा सेट में सबसे अधिक दोहराया जाने वाला मान है।

इसलिए, एक सांख्यिकीय डेटा सेट के मोड की गणना करने के लिए, बस नमूने में प्रत्येक डेटा तत्व के प्रकट होने की संख्या की गणना करें, और सबसे अधिक दोहराया गया डेटा मोड होगा।

मोड का उपयोग सांख्यिकीय वितरण को परिभाषित करने के लिए किया जाता है, क्योंकि सबसे अधिक दोहराया गया मान आमतौर पर वितरण के केंद्र में होता है।

मोड को सांख्यिकीय मोड या मोडल वैल्यू भी कहा जा सकता है। इसी प्रकार, जब डेटा को अंतरालों में समूहीकृत किया जाता है, तो सबसे अधिक दोहराया जाने वाला अंतराल मोडल अंतराल या मोडल वर्ग होता है।

सामान्य तौर पर, मो शब्द का उपयोग सांख्यिकीय मोड के प्रतीक के रूप में किया जाता है, उदाहरण के लिए, वितरण मोड एक्स मो (एक्स) है।

ध्यान रखें कि मोड केंद्र स्थिति के साथ-साथ मध्यिका और माध्य का एक सांख्यिकीय माप है। नीचे हम देखेंगे कि इनमें से प्रत्येक सांख्यिकीय उपाय का क्या अर्थ है।

सांख्यिकी में मोड प्रकार

आंकड़ों में, कई प्रकार के मोड होते हैं जिन्हें सबसे अधिक दोहराए गए मानों की संख्या के अनुसार वर्गीकृत किया जाता है:

यूनिमॉडल मोड : अधिकतम संख्या में दोहराव के साथ केवल एक मान होता है। उदाहरण के लिए, [1, 4, 2, 4, 5, 3]।
बिमोडल मोड : दोहराव की अधिकतम संख्या दो अलग-अलग मानों पर होती है, और दोनों मान समान संख्या में दोहराए जाते हैं। उदाहरण के लिए, [2, 6, 7, 2, 3, 6, 9]।
मल्टीमॉडल मोड : तीन या अधिक मानों में दोहराव की अधिकतम संख्या समान होती है। उदाहरण के लिए, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1]।

सांख्यिकीय मोड कैसे खोजें

किसी डेटासेट का सांख्यिकीय मोड खोजने के लिए, आपको निम्नलिखित चरणों का पालन करना होगा:

डेटा को क्रम में रखें. यह कदम अनिवार्य नहीं है, लेकिन इससे संख्याओं की गिनती आसान हो जाएगी।
गिनें कि प्रत्येक संख्या कितनी बार प्रकट होती है।
जो संख्या सबसे अधिक बार दिखाई देती है वह सांख्यिकीय विधा है।

सांख्यिकीय पद्धति के उदाहरण

आंकड़ों में फैशन की परिभाषा को ध्यान में रखते हुए, नीचे आप प्रत्येक प्रकार के फैशन का एक उदाहरण देख सकते हैं ताकि आप अवधारणा को बेहतर ढंग से समझ सकें।

यूनिमॉडल मोड का उदाहरण

निम्नलिखित डेटासेट का मोड क्या है?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

संख्याओं को क्रमबद्ध नहीं किया गया है, इसलिए बहुलक ढूंढना आसान बनाने के लिए हम उन्हें पहले क्रमित करेंगे।

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

संख्या 2 और 9 दो बार आती हैं, लेकिन संख्या 5 तीन बार दोहराई जाती है। इसलिए, डेटा श्रृंखला का मोड संख्या 5 है।

$Mo=5$

बिमोडल मोड का उदाहरण

निम्नलिखित डेटा सेट के मोड की गणना करें:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

सबसे पहले हम संख्याओं को क्रम में रखते हैं:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

जैसा कि आप देख सकते हैं, संख्या 6 और संख्या 8 कुल मिलाकर चार बार आती हैं, जो पुनरावृत्ति की अधिकतम संख्या है। इसलिए, इस मामले में यह एक द्विमोडल मोड है और दो संख्याएँ डेटासेट का मोड हैं:

$Mo=\{ 6 \ ; \ 8\}$

मल्टीमॉडल मोड का उदाहरण

निम्नलिखित डेटासेट मोड खोजें:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

चूँकि बहुत सारा डेटा है, इसलिए हम इसे गिनना आसान बनाने के लिए पहले इसे आरोही क्रम में क्रमबद्ध करते हैं:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

सर्वाधिक दोहराई जाने वाली संख्याएँ 20, 27 और 31 हैं, तीनों संख्याएँ पाँच बार दोहराई जाती हैं। इसलिए इस उदाहरण का मोड मल्टीमॉडल है।

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

फैशन कैलकुलेटर

इसके मोड की गणना करने के लिए किसी भी सांख्यिकीय नमूने से डेटा को निम्नलिखित ऑनलाइन कैलकुलेटर में दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

समूहीकृत डेटा के लिए मोड

जब हमारे पास डेटा को अंतराल के रूप में समूहीकृत किया जाता है, तो हम वास्तव में नहीं जानते हैं कि डेटा का प्रत्येक टुकड़ा कितनी बार दोहराया जाता है, हम केवल प्रत्येक अंतराल की आवृत्ति जानते हैं।

इस प्रकार, अंतरालों में समूहीकृत डेटा के मोड की गणना करने के लिए, हमें निम्नलिखित सूत्र का उपयोग करना चाहिए :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

सोना:

L _i मोडल अंतराल (उच्चतम निरपेक्ष आवृत्ति अंतराल) की निचली सीमा है।
f _i मोडल अंतराल की पूर्ण आवृत्ति है।
f _i-1 मोडल से पहले के अंतराल की पूर्ण आवृत्ति है।
f _i+1 मोडल के बाद अंतराल की पूर्ण आवृत्ति है।
A _i मोडल अंतराल की चौड़ाई है।

उदाहरण के तौर पर, नीचे आपने एक अभ्यास हल किया है जिसमें अंतरालों में समूहीकृत डेटा के मोड की गणना की जाती है:

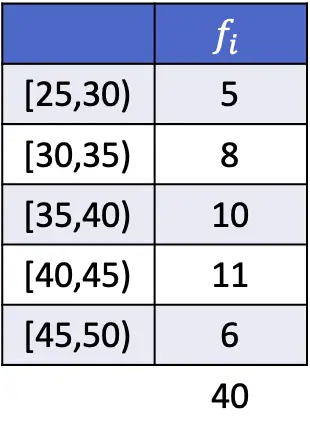
समूहीकृत डेटा के लिए सांख्यिकीय मोड का उदाहरण

इस मामले में, मोडल अंतराल [40,45) है, क्योंकि यह सबसे बड़ी निरपेक्ष आवृत्ति वाला अंतराल है। इसलिए, समूहीकृत डेटा के लिए मोड सूत्र पैरामीटर हैं:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

इसलिए हम अंतरालों में समूहीकृत डेटा के मोड को निर्धारित करने के लिए सूत्र लागू करते हैं और हम गणना करते हैं:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

मोड, माध्य और माध्यिका के बीच अंतर

इस अंतिम भाग में हम देखेंगे कि बहुलक, माध्य और माध्यिका के बीच क्या अंतर है। चूंकि ये तीनों केंद्रीय स्थिति के सांख्यिकीय माप हैं, इसलिए इनका अर्थ अलग-अलग है।

जैसा कि पूरे लेख में बताया गया है, गणित में मोड किसी डेटा सेट में सबसे अधिक दोहराया जाने वाला मान है।

दूसरा, माध्य सभी सांख्यिकीय डेटा का औसत मूल्य है। इस प्रकार, कुछ डेटा का औसत प्राप्त करने के लिए, आपको सभी डेटा को जोड़ना होगा और फिर परिणाम को अवलोकनों की संख्या से विभाजित करना होगा।

और अंत में, माध्यिका वह मान है जो डेटा ऑर्डर करते समय केंद्रीय स्थान पर रहता है।

इस प्रकार, तीन सांख्यिकीय उपाय संभाव्यता वितरण को परिभाषित करने में मदद करते हैं, क्योंकि वे इसके केंद्रीय मूल्यों का एक विचार प्रदान करते हैं। लेकिन ध्यान रखें कि ऐसा कोई एक माप नहीं है जो दूसरे से बेहतर हो, उनका मतलब बस अलग-अलग अवधारणाएं हैं।

फैशन गुण

फैशन गुण हैं:

मोड मात्रात्मक चर और गुणात्मक चर दोनों में पाया जा सकता है।
यदि हम एक यादृच्छिक चर में एक रैखिक परिवर्तन लागू करते हैं, तो लागू संचालन के आधार पर माध्य का मान बदल जाएगा।

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

सामान्य तौर पर, मोड आउटलेर्स के प्रति असंवेदनशील है।
यदि सभी मानों की आवृत्ति समान है, तो कोई मोड नहीं है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने