सांख्यिकीय सूत्र

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 1, 2023 आंकड़े शून्य टिप्पणियां

यहां आपको मुख्य सांख्यिकीय सूत्र मिलेंगे। हम आपको अपने लेखों से भी जोड़े रखते हैं जिसमें आप प्रत्येक सांख्यिकीय सूत्र के अनुप्रयोग के उदाहरण देख सकते हैं और इसके अलावा, आप एक ऑनलाइन कैलकुलेटर का उपयोग कर सकते हैं ताकि आपको गणना न करनी पड़े और सीधे सूत्र का परिणाम जान सकें।

केंद्रीय प्रवृत्ति के सांख्यिकीय माप के सूत्र

आधा

औसत की गणना करने के लिए, सभी मान जोड़ें और फिर डेटा की कुल संख्या से विभाजित करें। इसलिए औसत का सूत्र इस प्रकार है:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

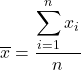
सांख्यिकी में माध्य को अंकगणितीय माध्य या औसत के रूप में भी जाना जाता है।

➤ देखें: अंकगणित माध्य कैलकुलेटर

मंझला

माध्यिका सबसे छोटे से लेकर सबसे बड़े तक क्रमित सभी डेटा का मध्य मान है। दूसरे शब्दों में, माध्य क्रमित डेटा सेट को दो बराबर भागों में विभाजित करता है।

माध्यिका की गणना इस बात पर निर्भर करती है कि डेटा की कुल संख्या सम है या विषम:

यदि डेटा की कुल संख्या विषम है, तो माध्यिका वह मान होगा जो डेटा के ठीक बीच में आता है। कहने का तात्पर्य यह है कि वह मान जो क्रमबद्ध डेटा की स्थिति (n+1)/2 में है।

$Me=x_{\frac{n+1}{2}$

यदि डेटा बिंदुओं की कुल संख्या सम है, तो माध्य केंद्र में स्थित दो डेटा बिंदुओं का औसत होगा। यानी उन मानों का अंकगणितीय औसत जो ऑर्डर किए गए डेटा के स्थानों n/2 और n/2+1 पर पाए जाते हैं।

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

सोना

$n$

नमूने में डेटा की कुल संख्या है और प्रतीक मी माध्यिका को इंगित करता है।

➤ देखें: माध्यिका कैलकुलेटर

पहनावा

आँकड़ों में, मोड डेटा सेट में वह मान है जिसकी निरपेक्ष आवृत्ति सबसे अधिक है, अर्थात, मोड डेटा सेट में सबसे अधिक दोहराया जाने वाला मान है।

इसलिए, मोड के लिए कोई विशिष्ट सूत्र नहीं है, लेकिन सांख्यिकीय डेटा सेट के मोड की गणना करने के लिए, बस नमूने में प्रत्येक डेटा तत्व दिखाई देने की संख्या की गणना करें, और सबसे अधिक दोहराया गया डेटा मोड होगा।

मोड को सांख्यिकीय मोड या मोडल वैल्यू भी कहा जा सकता है।

➤ देखें: फैशन कैलकुलेटर

फैलाव के सांख्यिकीय माप के लिए सूत्र

मानक विचलन

मानक विचलन, जिसे मानक विचलन भी कहा जाता है, डेटा श्रृंखला के विचलन के वर्गों के योग के वर्गमूल को अवलोकनों की कुल संख्या से विभाजित करने के बराबर होता है।

इसलिए, मानक विचलन का सूत्र है:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ देखें: मानक विचलन कैलकुलेटर

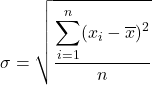
झगड़ा

विचरण कुल अवलोकनों की संख्या पर अवशेषों के वर्गों के योग के बराबर है। इस सांख्यिकीय मीट्रिक का सूत्र इस प्रकार है:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

सोना:

$X$

वह यादृच्छिक चर है जिसके लिए आप विचरण की गणना करना चाहते हैं।
$x_i$

डेटा मान है

$i$

.
$n$

प्रेक्षणों की कुल संख्या है.
$\overline{X}$

यादृच्छिक चर का माध्य है

$X$

.

➤ देखें: गैप कैलकुलेटर

गुणांक का परिवर्तन

आंकड़ों में, भिन्नता का गुणांक फैलाव का एक माप है जिसका उपयोग इसके माध्य के सापेक्ष डेटा सेट के फैलाव को निर्धारित करने के लिए किया जाता है। भिन्नता के गुणांक की गणना डेटा के मानक विचलन को उसके माध्य से विभाजित करके की जाती है, फिर मान को प्रतिशत के रूप में व्यक्त करने के लिए 100 से गुणा किया जाता है।

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ देखें: भिन्नता गुणांक कैलकुलेटर

साफ

सांख्यिकीय सीमा फैलाव का एक माप है जो एक नमूने में डेटा के अधिकतम मूल्य और न्यूनतम मूल्य के बीच अंतर को इंगित करता है। इसलिए, किसी जनसंख्या या सांख्यिकीय नमूने की सीमा की गणना करने के लिए, अधिकतम मूल्य को न्यूनतम मूल्य से घटाया जाना चाहिए।

$R=\text{M\'ax}-\text{M\'in}$

➤ देखें: सांख्यिकीय सीमा का उदाहरण

अन्तःचतुर्थक श्रेणी

अंतरचतुर्थक श्रेणी , जिसे अंतरचतुर्थक श्रेणी भी कहा जाता है, सांख्यिकीय फैलाव का एक माप है जो तीसरे और पहले चतुर्थक के बीच अंतर को इंगित करता है।

इसलिए, सांख्यिकीय डेटा सेट की अंतरचतुर्थक सीमा की गणना करने के लिए, आपको पहले तीसरा और पहला चतुर्थक ढूंढना होगा और फिर उन्हें घटाना होगा।

$IQR=Q_3-Q_1$

➤ देखें: इंटरक्वेर्टाइल रेंज कैलकुलेटर

मध्यम अंतर

माध्य विचलन , जिसे माध्य निरपेक्ष विचलन भी कहा जाता है, निरपेक्ष विचलन का औसत है। इसलिए औसत विचलन अंकगणित माध्य से प्रत्येक डेटा आइटम के विचलन के योग को डेटा आइटम की कुल संख्या से विभाजित करने के बराबर है।

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ देखें: औसत विचलन कैलकुलेटर

सांख्यिकीय स्थिति माप के लिए सूत्र

चतुर्थक

सांख्यिकी में, चतुर्थक वे तीन मान हैं जो क्रमित डेटा के एक सेट को चार बराबर भागों में विभाजित करते हैं। इस प्रकार, पहला, दूसरा और तीसरा चतुर्थक सभी सांख्यिकीय डेटा का क्रमशः 25%, 50% और 75% प्रतिनिधित्व करता है।

चतुर्थक को बड़े Q और चतुर्थक सूचकांक द्वारा दर्शाया जाता है, इसलिए पहला चतुर्थक Q ₁ है, दूसरा चतुर्थक Q ₂ है, और तीसरा चतुर्थक Q ₃ है।

चतुर्थक सूत्र है:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

कृपया ध्यान दें: यह सूत्र हमें चतुर्थक की स्थिति बताता है, न कि चतुर्थक का मान। चतुर्थक सूत्र द्वारा प्राप्त स्थिति पर स्थित डेटा होगा।

हालाँकि, कभी-कभी इस सूत्र का परिणाम हमें दशमलव संख्या देगा। इसलिए हमें दो मामलों में अंतर करना चाहिए जो इस बात पर निर्भर करता है कि परिणाम दशमलव संख्या है या नहीं:

यदि सूत्र का परिणाम दशमलव भाग के बिना एक संख्या है, तो चतुर्थक वह डेटा है जो उपरोक्त सूत्र द्वारा प्रदान की गई स्थिति में है।
यदि सूत्र परिणाम दशमलव भाग वाली एक संख्या है, तो चतुर्थक मान की गणना निम्न सूत्र का उपयोग करके की जाती है:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

जहाँ x _i और x _i+1 उन स्थितियों की संख्याएँ हैं जिनके बीच पहले सूत्र द्वारा प्राप्त संख्या स्थित है, और d पहले सूत्र द्वारा प्राप्त संख्या का दशमलव भाग है।

➤ देखें: चतुर्थक कैलकुलेटर

दशमलव

आंकड़ों में, डेसील्स वे नौ मान हैं जो ऑर्डर किए गए डेटा के एक सेट को दस बराबर भागों में विभाजित करते हैं। ताकि पहला, दूसरा, तीसरा,… दशमलव नमूना या जनसंख्या का 10%, 20%, 30%,… का प्रतिनिधित्व करता हो।

डेसील को बड़े अक्षर D और डेसील इंडेक्स द्वारा दर्शाया जाता है, अर्थात, पहला डेसील D ₁ है, दूसरा डेसील D ₂ है, तीसरा डेसील D ₃ है, आदि।

दशमलव सूत्र इस प्रकार है:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

कृपया ध्यान दें: यह सूत्र हमें दशमलव की स्थिति बताता है, न कि दशमलव का मान। दशमलव सूत्र द्वारा प्राप्त स्थिति पर स्थित डेटा होगा।

हालाँकि, कभी-कभी इस सूत्र का परिणाम हमें दशमलव संख्या देगा, इसलिए हमें दो मामलों में अंतर करना होगा, यह इस बात पर निर्भर करेगा कि परिणाम दशमलव संख्या है या नहीं:

यदि सूत्र का परिणाम दशमलव भाग के बिना एक संख्या है, तो दशमलव उपरोक्त सूत्र द्वारा प्रदान की गई स्थिति में स्थित डेटा है।
यदि सूत्र का परिणाम दशमलव भाग वाली एक संख्या है, तो दशमलव मान की गणना निम्न सूत्र का उपयोग करके की जाती है:

$D=x_i+d\cdot (x_{i+1}-x_i)$

➤ देखें: डेसील कैलकुलेटर

प्रतिशतक

आंकड़ों में, प्रतिशतक वे मान हैं जो ऑर्डर किए गए डेटा के एक सेट को एक सौ बराबर भागों में विभाजित करते हैं। तो, एक प्रतिशतक उस मान को इंगित करता है जिसके नीचे डेटा सेट का एक प्रतिशत गिरता है।

प्रतिशतक को बड़े अक्षर P और प्रतिशतक सूचकांक द्वारा दर्शाया जाता है, अर्थात, पहला प्रतिशतक P ₁ है, 40वाँ प्रतिशतक P ₄₀ है, 79वाँ प्रतिशतक P ₇₉ है, आदि।

प्रतिशतक सूत्र है:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

कृपया ध्यान दें: यह सूत्र हमें प्रतिशतक की स्थिति बताता है, लेकिन उसका मान नहीं। प्रतिशतक सूत्र द्वारा प्राप्त स्थिति पर स्थित डेटा होगा।

यदि सूत्र का परिणाम दशमलव भाग के बिना एक संख्या है, तो प्रतिशतक उस डेटा से मेल खाता है जो उपरोक्त सूत्र द्वारा प्रदान की गई स्थिति में है।
यदि सूत्र परिणाम दशमलव भाग वाली एक संख्या है, तो सटीक प्रतिशत मान की गणना निम्न सूत्र का उपयोग करके की जाती है:

$P=x_i+d\cdot (x_{i+1}-x_i)$

➤ देखें: प्रतिशत कैलकुलेटर

सांख्यिकीय आकार माप सूत्र

विषमता गुणांक

तिरछापन गुणांक, या तिरछापन सूचकांक, एक सांख्यिकीय गुणांक है जिसका उपयोग किसी वितरण की तिरछापन निर्धारित करने के लिए किया जाता है। तो, विषमता गुणांक की गणना करके, आप वितरण की विषमता के प्रकार को बिना उसका ग्राफिकल प्रतिनिधित्व किए जान सकते हैं।

विषमता गुणांक का सूत्र इस प्रकार है:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

समान रूप से, फिशर असममिति गुणांक की गणना के लिए निम्नलिखित दो सूत्रों में से किसी एक का उपयोग किया जा सकता है:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

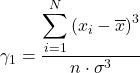
सोना

$E$

गणितीय अपेक्षा है,

$\overline{x}$

अंकगणित माध्य,

$\sigma$

मानक विचलन और

$n$

डेटा की कुल संख्या.

➤ देखें: विषमता गुणांक

कर्टोसिस गुणांक

कर्टोसिस, जिसे तीक्ष्णता भी कहा जाता है, इंगित करता है कि वितरण अपने माध्य के आसपास कितना केंद्रित है। दूसरे शब्दों में, कर्टोसिस इंगित करता है कि वितरण तीव्र या सपाट है। विशेष रूप से, किसी वितरण का कुर्टोसिस जितना अधिक होगा, वह उतना ही तेज़ (या तेज़) होगा।

कर्टोसिस गुणांक का सूत्र इस प्रकार है:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

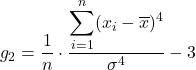
सोना

$x_i$

अवलोकन के अनुरूप मूल्य है

$i$

$\overline{x}$

अंकगणित माध्य,

$\sigma$

मानक विचलन और

$n$

डेटा की कुल संख्या.

➤ देखें: फ़्लैटनिंग गुणांक कैलकुलेटर

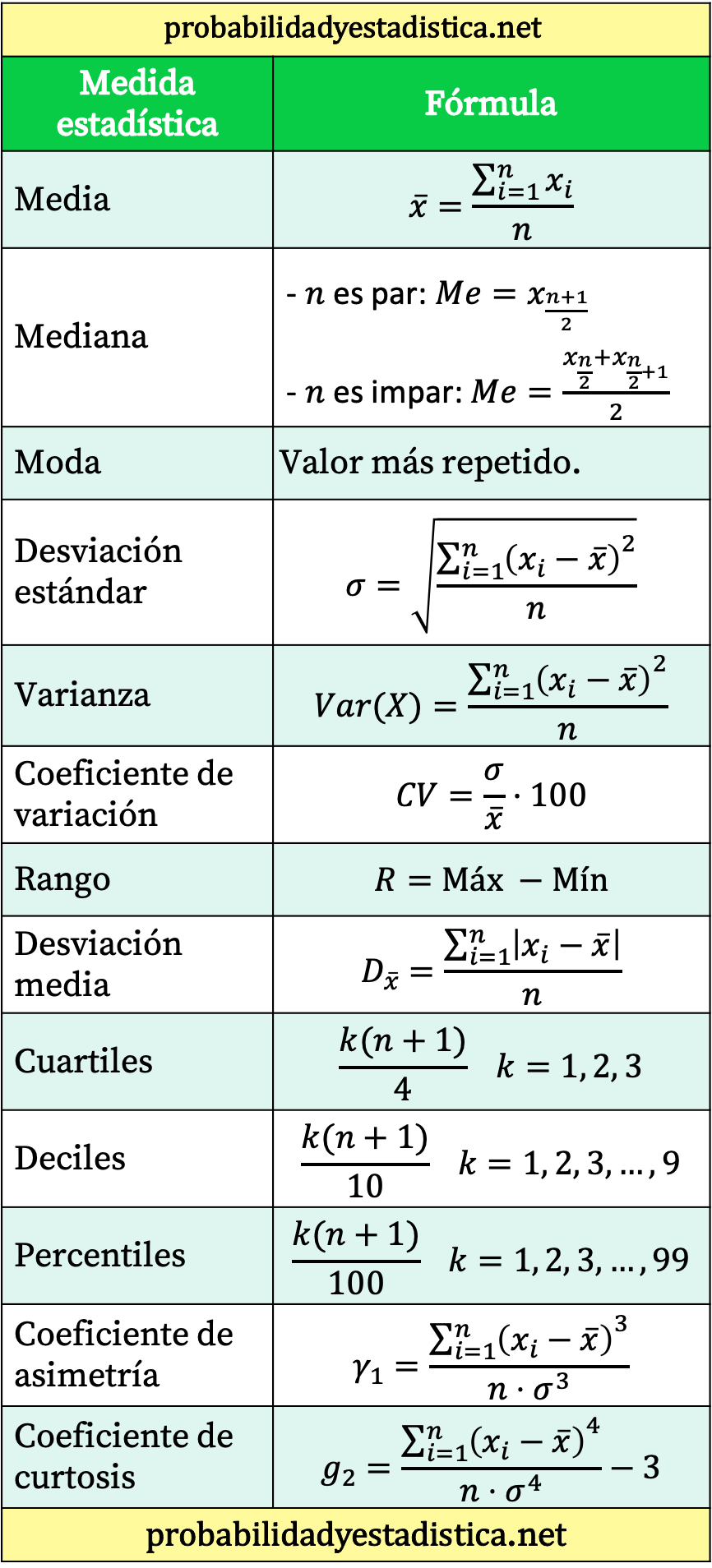
सभी सांख्यिकीय सूत्रों की सारांश तालिका

अंत में, हम आपके लिए एक तालिका छोड़ते हैं जो मुख्य सांख्यिकीय सूत्रों का सारांश प्रस्तुत करती है।

➤ देखें: संभाव्यता सूत्र

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

केंद्रीय प्रवृत्ति के सांख्यिकीय माप के सूत्र

आधा

मंझला

पहनावा

फैलाव के सांख्यिकीय माप के लिए सूत्र

मानक विचलन

झगड़ा

गुणांक का परिवर्तन

साफ

अन्तःचतुर्थक श्रेणी

मध्यम अंतर

सांख्यिकीय स्थिति माप के लिए सूत्र

चतुर्थक

दशमलव

प्रतिशतक

सांख्यिकीय आकार माप सूत्र

विषमता गुणांक

कर्टोसिस गुणांक

सभी सांख्यिकीय सूत्रों की सारांश तालिका

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने