कार्यक्षेत्र प्रतिबंध क्या है?

अक्सर आंकड़ों में हम दो चरों के बीच संबंध को मापना चाहते हैं। इससे हमें निम्नलिखित समझने में मदद मिलती है:

• दो चरों के बीच संबंध की दिशा . जैसे-जैसे एक चर बढ़ता है, क्या दूसरा चर बढ़ता या घटता है?
• दो चरों के बीच संबंध की ताकत . दोनों वेरिएबल्स का मान कितना बदलता है?

दुर्भाग्य से, एक समस्या जो दो चरों के बीच सहसंबंध को मापते समय उत्पन्न हो सकती है उसे सीमा प्रतिबंध कहा जाता है। ऐसा तब होता है जब किसी एक चर के लिए मापे गए मानों की सीमा किसी कारण से प्रतिबंधित होती है।

उदाहरण के लिए, मान लीजिए कि हम किसी विशेष स्कूल में अध्ययन के घंटों और छात्रों के परीक्षा अंकों के बीच संबंध को मापना चाहते हैं।

यदि हम स्कूल के सभी 1,000 छात्रों के लिए इन दो चर पर डेटा एकत्र करते हैं, तो हम पा सकते हैं कि अध्ययन के घंटों और परीक्षा के अंकों के बीच संबंध 0.73 है।

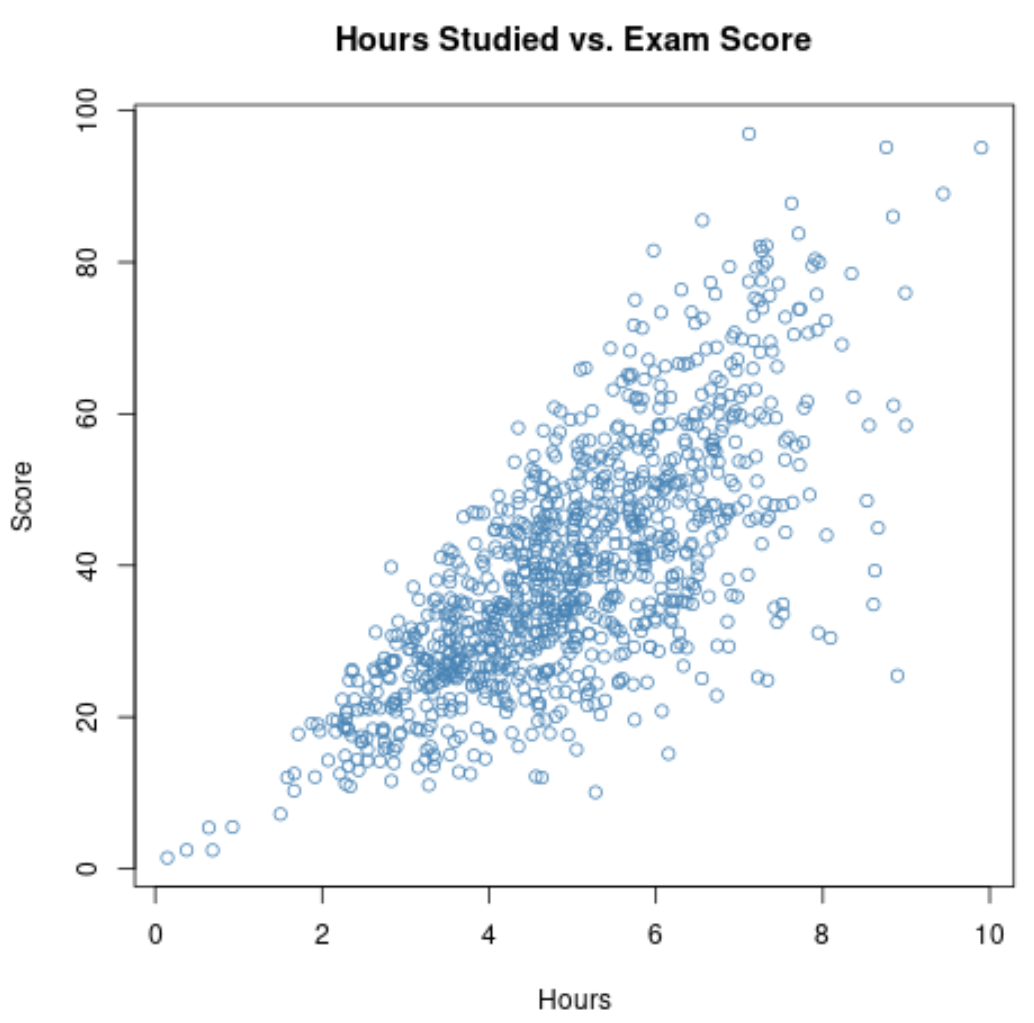
यह सहसंबंध काफी अधिक है, जो दो चरों के बीच एक मजबूत सकारात्मक संबंध का संकेत देता है। जैसे-जैसे छात्र अधिक अध्ययन करते हैं, वे परीक्षाओं में बेहतर प्रदर्शन करते हैं।

हालाँकि, मान लें कि हम केवल ऑनर्स पाठ्यक्रमों के छात्रों का डेटा एकत्र करते हैं। हो सकता है कि इन सभी छात्रों ने कम से कम 6 घंटे तक पढ़ाई की हो.

इसलिए, यदि हम इन छात्रों के लिए अध्ययन किए गए घंटों और परीक्षा अंकों के बीच सहसंबंध की गणना करते हैं, तो हम अध्ययन किए गए परिवर्तनीय घंटों के लिए एक संकीर्ण सीमा का उपयोग करेंगे।

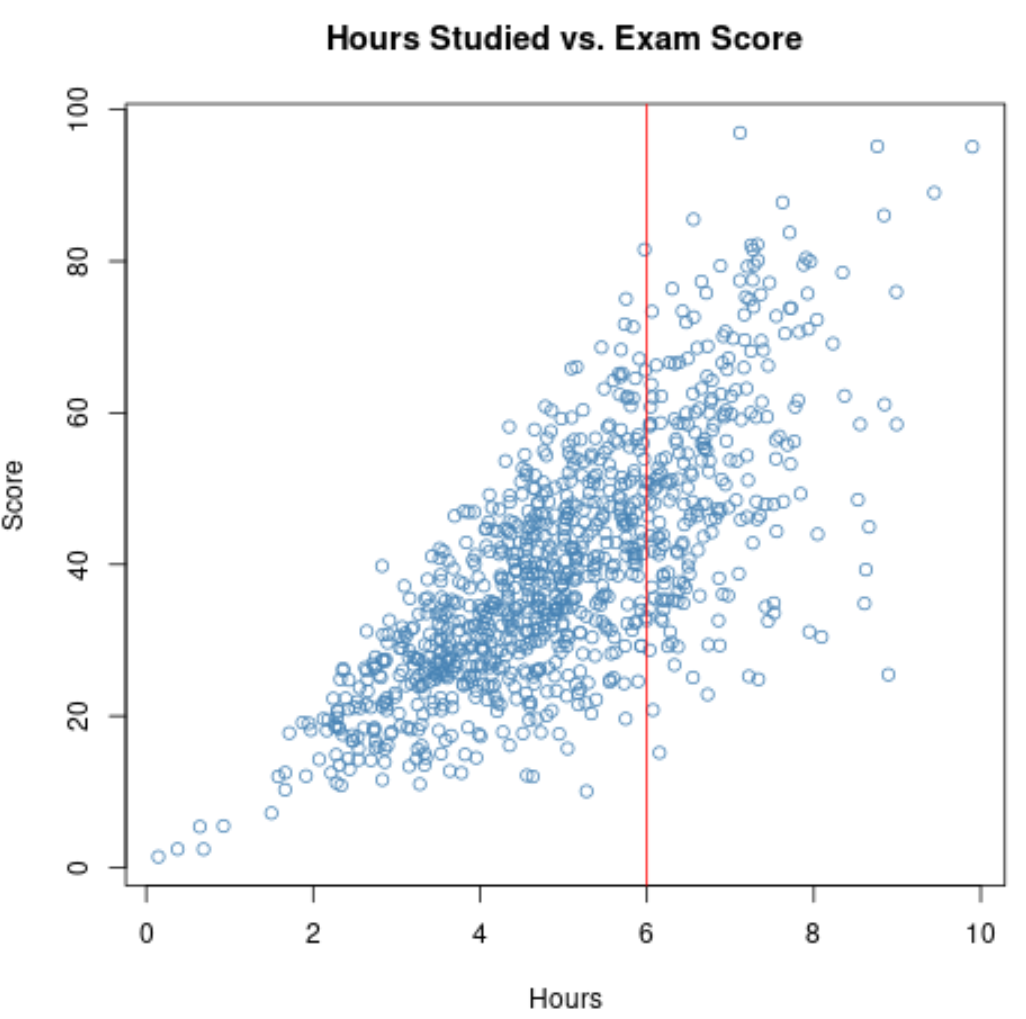
यदि हम उस सीमा के लिए स्कैटरप्लॉट पर ज़ूम इन करते हैं जहां घंटे 6 से अधिक हैं, तो प्लॉट इस तरह दिखता है:

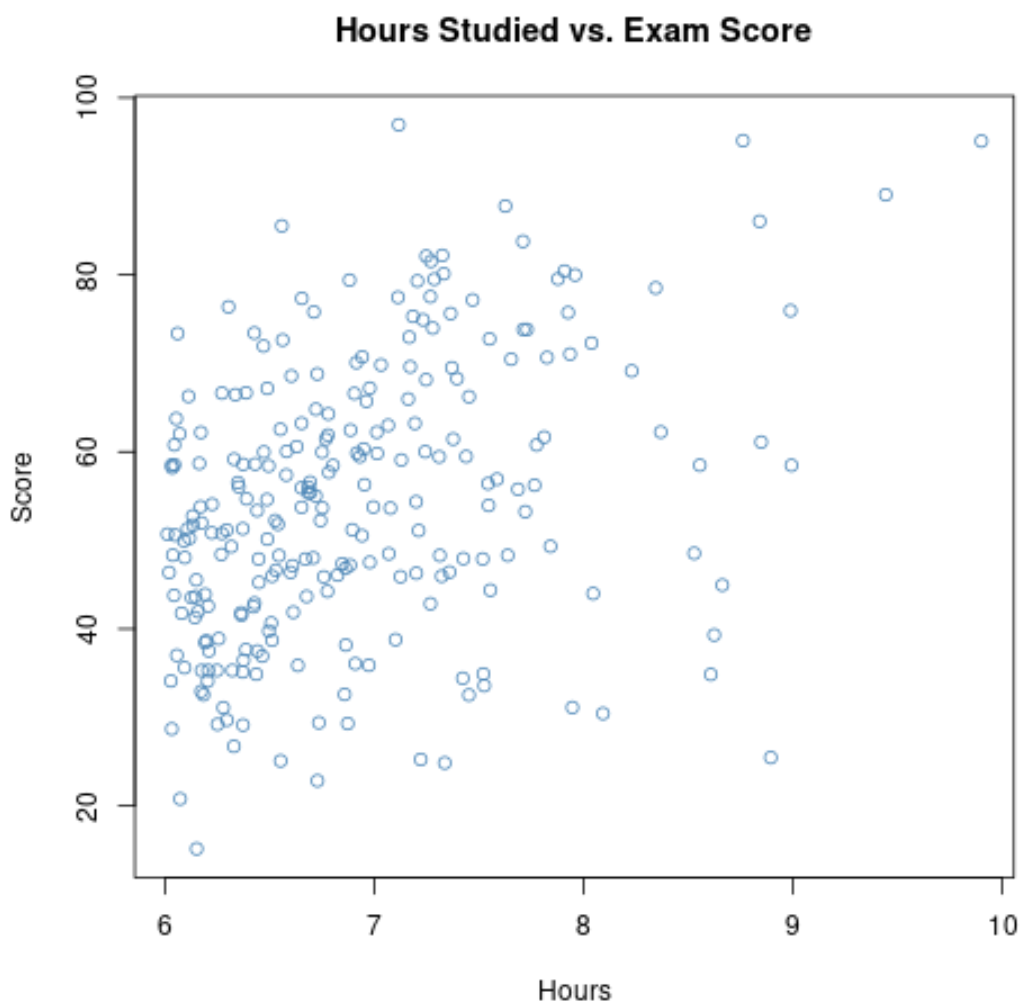
इस ग्राफ़ पर दो चरों के बीच सहसंबंध 0.37 है, जो 0.73 से काफी कम है।

इस प्रकार, यदि हमने केवल ऑनर्स पाठ्यक्रमों में छात्रों के लिए अध्ययन किए गए घंटों और परीक्षा अंकों पर डेटा एकत्र किया है, तो हम मान सकते हैं कि अध्ययन किए गए घंटों और परीक्षा अंकों के बीच एक कमजोर संबंध है।

हालाँकि, यह परिणाम भ्रामक होगा क्योंकि हमने एक चर के लिए प्रतिबंधित सीमा का उपयोग किया है।

प्रतिबंधित सीमा के वास्तविक दुनिया के उदाहरण

कई अलग-अलग शोध अध्ययनों में प्रतिबंधित सीमा की समस्या व्यवहार में उत्पन्न हो सकती है। यहां कुछ उदाहरण दिए गए हैं:

1. उच्च प्रदर्शन वाले एथलीटों पर अध्ययन । शोधकर्ताओं को यह अध्ययन करने में रुचि हो सकती है कि क्या एक निश्चित प्रशिक्षण कार्यक्रम एक निश्चित मानक कार्यक्रम की तुलना में अधिक मांसपेशी द्रव्यमान पैदा करता है।

यदि शोधकर्ता केवल विशिष्ट एथलीटों पर डेटा एकत्र करते हैं, तो संभावना है कि इन सभी एथलीटों के पास पहले से ही उच्च मांसपेशी द्रव्यमान है। इसलिए प्रशिक्षण कार्यक्रम और उत्पादित मांसपेशी द्रव्यमान के बीच सहसंबंध की गणना करने के लिए मूल्यों की एक संकीर्ण श्रृंखला उपलब्ध होगी।

2. उच्च उपलब्धि प्राप्त करने वाले विद्यार्थियों का अध्ययन। शोधकर्ता यह अध्ययन करना चाह सकते हैं कि किसी निश्चित शिक्षण कार्यक्रम का ग्रेड पर सकारात्मक प्रभाव पड़ता है या नहीं। स्वभाव से, अपने ग्रेड में सुधार करने और ट्यूशन कार्यक्रम में भाग लेने के इच्छुक छात्र पहले से ही उच्च उपलब्धि हासिल करने वाले छात्र हो सकते हैं।

इसलिए इन छात्रों के ग्रेड में सुधार की ज्यादा गुंजाइश नहीं हो सकती है। जब शोधकर्ता ट्यूशन कार्यक्रम में बिताए गए घंटों और परिणामी ग्रेड वृद्धि के बीच सहसंबंध की गणना करते हैं, तो वास्तविक सहसंबंध को कम करके आंका जा सकता है क्योंकि ग्रेड सुधार की गुंजाइश सीमित कर दी गई है।

प्रतिबंधित सीमाओं का हिसाब कैसे दें

प्रतिबंधित सीमाओं को ध्यान में रखने का एक लोकप्रिय तरीका थार्नडाइक केस 2 के रूप में जाना जाता है, जो मनोचिकित्सक रॉबर्ट एल. थार्नडाइक द्वारा विकसित एक सूत्र है।

यह सूत्र दो चरों के बीच वास्तविक सहसंबंध का अनुमान प्रदान करता है और निम्नलिखित गणना का उपयोग करता है:

सच्चा सहसंबंध = √(1-(एसडी ² _{वाई प्रतिबंधित} -एसडी ² _{वाई अप्रतिबंधित} )) * (1-आर ² _{प्रतिबंधित} )

सोना:

• एसडी ² _{प्रतिबंधित वाई} : प्रतिक्रिया चर वाई पर उपलब्ध डेटा का वर्ग मानक विचलन।
• _{अप्रतिबंधित} एसडी ² वाई: जनसंख्या के लिए प्रतिक्रिया चर का ज्ञात वर्ग मानक विचलन।
• आर ² _{प्रतिबंधित} : उपलब्ध प्रतिबंधित डेटा पर द्विघात सहसंबंध।

यह सूत्र दो चरों के बीच वास्तविक सहसंबंध के निष्पक्ष अनुमान लगाने में प्रभावी साबित हुआ है, जब उनमें से एक चर एक प्रतिबंधित सीमा से ग्रस्त होता है।

ध्यान दें कि इस सूत्र का उपयोग करने के लिए, आपके पास प्रतिक्रिया चर के लिए वास्तविक जनसंख्या मानक विचलन का अनुमान होना चाहिए।