स्नेडेकोर एफ वितरण
यह आलेख बताता है कि स्नेडेकोर एफ वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसके अतिरिक्त, आप स्नेडेकोर एफ वितरण ग्राफ और इसके सांख्यिकीय गुण क्या हैं, यह देख पाएंगे।
स्नेडेकोर एफ वितरण क्या है?
स्नेडेकोर एफ वितरण , जिसे फिशर-स्नेडेकोर एफ वितरण या केवल एफ वितरण भी कहा जाता है, एक सतत संभाव्यता वितरण है जिसका उपयोग सांख्यिकीय अनुमान में किया जाता है, विशेष रूप से विचरण के विश्लेषण में।
स्नेडेकोर एफ वितरण के गुणों में से एक यह है कि इसे दो वास्तविक मापदंडों, एम और एन के मूल्य से परिभाषित किया गया है, जो उनकी स्वतंत्रता की डिग्री को दर्शाता है। इस प्रकार, स्नेडेकोर वितरण F का प्रतीक F m,n है, जहां m और n वे पैरामीटर हैं जो वितरण को परिभाषित करते हैं।
![\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png "Rendered by QuickLaTeX.com")
फिशर-स्नेडेकोर एफ वितरण का नाम अंग्रेजी सांख्यिकीविद् रोनाल्ड फिशर और अमेरिकी सांख्यिकीविद् जॉर्ज स्नेडेकोर के नाम पर रखा गया है।
आंकड़ों में, फिशर-स्नेडेकोर एफ वितरण के विभिन्न अनुप्रयोग हैं। उदाहरण के लिए, फिशर-स्नेडेकोर एफ वितरण का उपयोग विभिन्न रैखिक प्रतिगमन मॉडल की तुलना करने के लिए किया जाता है, और इस संभाव्यता वितरण का उपयोग विचरण (एनोवा) के विश्लेषण में किया जाता है।
स्नेडेकोर एफ वितरण आरेख
एक बार जब हमने स्नेडेकोर एफ वितरण की परिभाषा देख ली, तो इसके घनत्व फ़ंक्शन का ग्राफ और इसकी संचयी संभावना का ग्राफ नीचे दिखाया गया है।
नीचे दिए गए ग्राफ़ में आप स्वतंत्रता की विभिन्न डिग्री के साथ स्नेडेकोर एफ वितरण के कई उदाहरण देख सकते हैं।
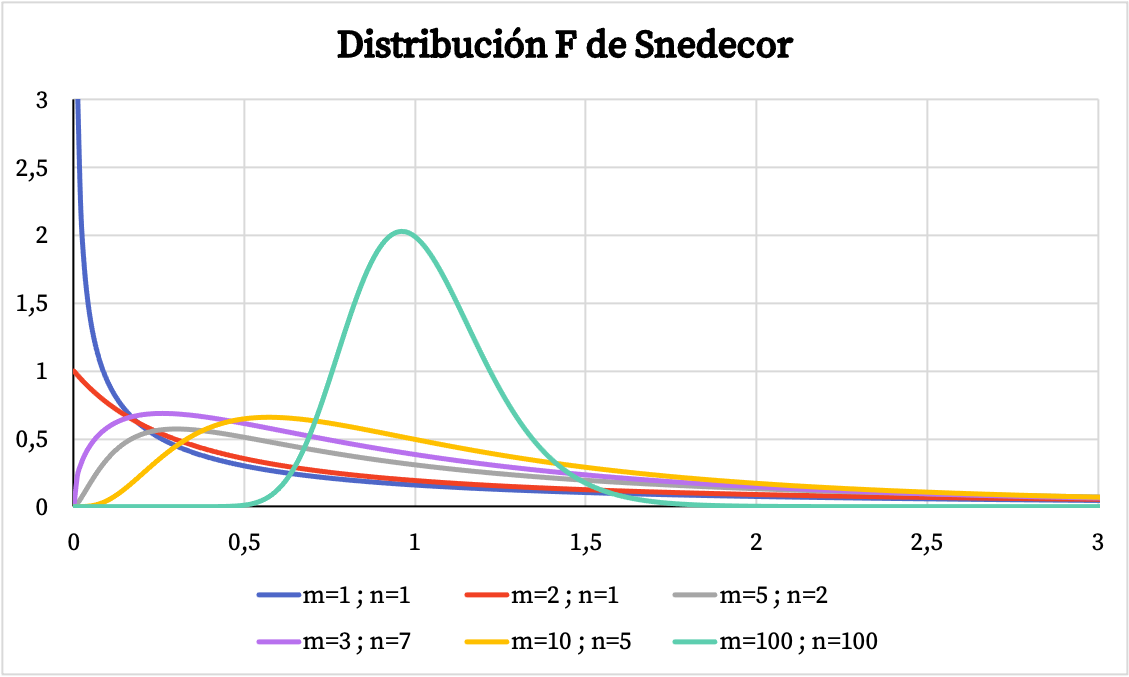
दूसरी ओर, नीचे दिए गए ग्राफ़ में आप देख सकते हैं कि स्नेडेकोर एफ वितरण के संचयी संभाव्यता फ़ंक्शन का ग्राफ़ इसके विशिष्ट मूल्यों के आधार पर कैसे भिन्न होता है।
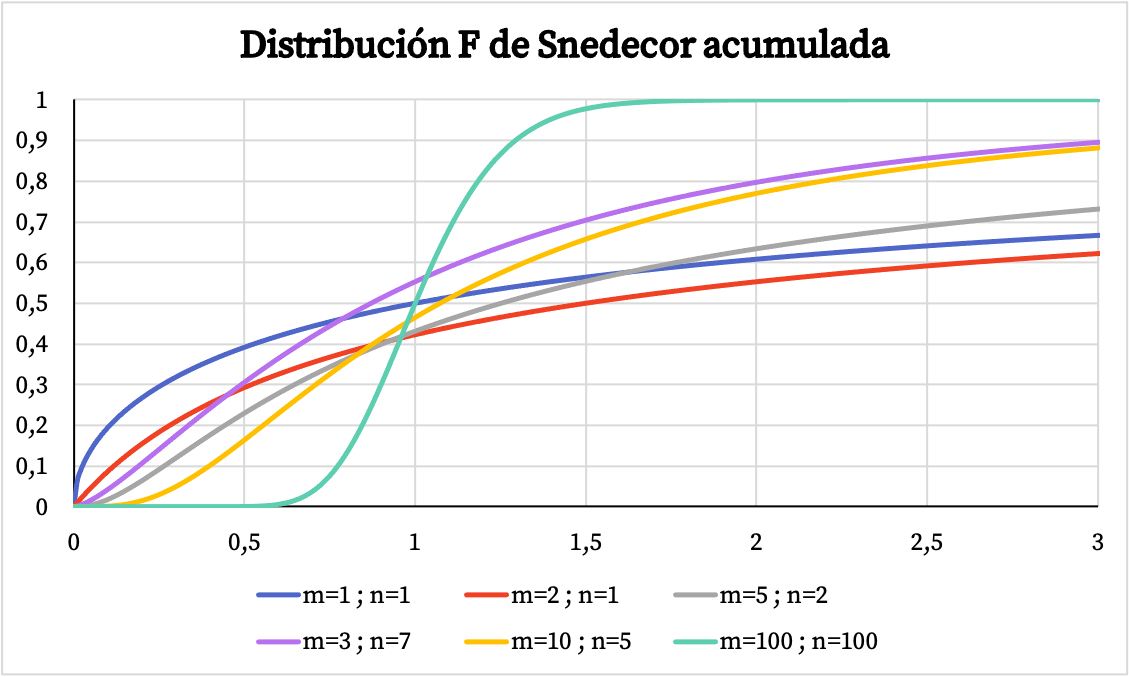
स्नेडेकोर एफ वितरण की विशेषताएं
अंत में, यह खंड स्नेडेकोर एफ वितरण की सबसे महत्वपूर्ण विशेषताओं को प्रस्तुत करता है।
- स्नेडेकोर एफ वितरण की स्वतंत्रता की डिग्री, एम और एन , दो पैरामीटर हैं जो वितरण के आकार को परिभाषित करते हैं। स्नेडेकोर एफ वितरण के ये विशिष्ट मान धनात्मक पूर्णांक हैं।
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> स्नेडेकोर एफ वितरण के डोमेन में शून्य से अधिक या उसके बराबर सभी वास्तविक संख्याएँ शामिल हैं।</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
- 2 से अधिक n के मानों के लिए, स्नेडेकोर F वितरण का माध्य n शून्य से 2 घटाने पर n के बराबर है।
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> जब पैरामीटर <em>n</em> 2 से अधिक है, तो स्नेडेकोर वितरण F के विचरण की गणना निम्न सूत्र को लागू करके की जा सकती है:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> यदि पैरामीटर <em>m</em> 2 से अधिक है, तो स्नेडेकोर वितरण F के मोड की गणना निम्नलिखित अभिव्यक्ति के साथ की जा सकती है:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
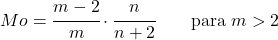
![\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png "Rendered by QuickLaTeX.com")
- यदि कोई चर स्वतंत्रता की डिग्री एम और एन के साथ स्नेडेकोर एफ वितरण का अनुसरण करता है, तो उक्त चर का व्युत्क्रम स्वतंत्रता की समान डिग्री के साथ स्नेडेकोर एफ वितरण का अनुसरण करता है लेकिन इसके मूल्यों के क्रम को बदलता है।
- छात्र वितरण का स्नेडेकोर एफ वितरण के साथ निम्नलिखित संबंध है:
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने