हिस्टोग्राम
यह आलेख बताता है कि हिस्टोग्राम क्या है, इसका उपयोग किस लिए किया जाता है और हिस्टोग्राम की व्याख्या कैसे की जाती है। इस प्रकार, आप जानेंगे कि हिस्टोग्राम कैसे बनाया जाता है और सभी प्रकार के हिस्टोग्राम के उदाहरण क्या हैं।
हिस्टोग्राम क्या है?
हिस्टोग्राम एक प्रकार का सांख्यिकीय चार्ट है जिसमें सांख्यिकीय डेटा का एक सेट आयताकार सलाखों द्वारा दर्शाया जाता है, जैसे कि हिस्टोग्राम में प्रत्येक बार अपनी संबंधित आवृत्ति के समानुपाती होता है।
हिस्टोग्राम का उपयोग निरंतर चर को ग्राफ़ करने के लिए किया जाता है, जैसे कि सांख्यिकीय नमूने का वजन। इसके अतिरिक्त, एक हिस्टोग्राम आपको वितरण के आकार को तुरंत देखने की अनुमति देता है।
आवृत्ति हिस्टोग्राम में प्रत्येक बार की चौड़ाई अंतराल की चौड़ाई के समानुपाती होती है और ऊँचाई अंतराल की आवृत्ति के समानुपाती होती है।
हिस्टोग्राम कैसे बनाएं
हिस्टोग्राम बनाने के चरण हैं:
- हिस्टोग्राम के क्षैतिज अक्ष को डेटा श्रृंखला के आधार पर समूहों में विभाजित करें।
- हिस्टोग्राम के ऊर्ध्वाधर अक्ष पर अंतराल आवृत्ति मानों को प्लॉट करें।
- प्रत्येक अंतराल के लिए, अंतराल की आवृत्ति के बराबर ऊंचाई वाली एक आयताकार पट्टी बनाएं। ध्यान दें कि लगातार दो अंतरालों की छड़ें स्पर्श करनी चाहिए।
हिस्टोग्राम उदाहरण
एक बार जब आप हिस्टोग्राम की परिभाषा और संबंधित सिद्धांत देख लेते हैं, तो नीचे आप एक स्पष्ट उदाहरण देख सकते हैं कि इस प्रकार का सांख्यिकीय ग्राफ़ कैसे बनाया जाता है।
- एक कपड़े की दुकान एक दिन के दौरान अलग-अलग कीमतों की 50 इकाइयाँ बेचती है, जैसा कि निम्नलिखित आवृत्ति तालिका में दिखाया गया है। रिकॉर्ड किए गए बिक्री डेटा से एक हिस्टोग्राम बनाएं।
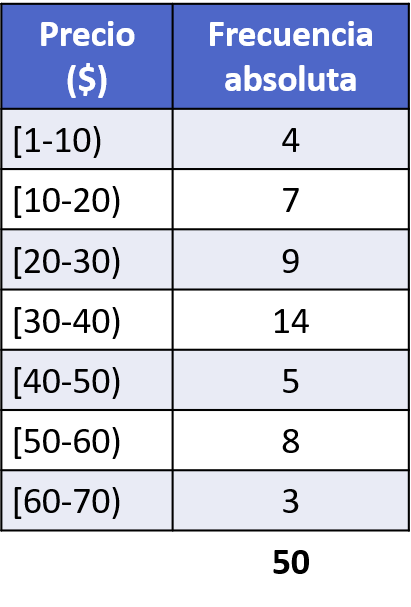
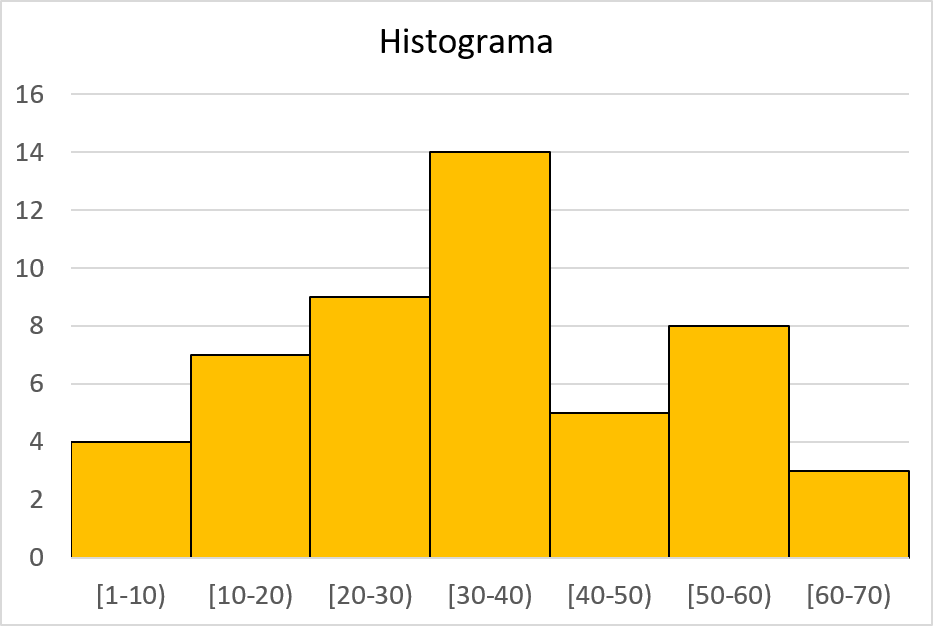
हिस्टोग्राम का प्रतिनिधित्व करने के लिए, हमें ऊपर बताए गए चरणों का पालन करना होगा। अर्थात्, हम पहले क्षैतिज अक्ष को डेटा के अंतराल के बराबर भागों में विभाजित करते हैं, फिर हम ऊर्ध्वाधर अक्ष के पैमाने को मापते हैं और अंत में, हम प्रत्येक अंतराल को उसकी पूर्ण आवृत्ति पर समान ऊंचाई के एक स्तंभ द्वारा दर्शाते हैं।
सापेक्ष आवृत्ति हिस्टोग्राम
सापेक्ष आवृत्ति हिस्टोग्राम एक प्रकार का हिस्टोग्राम है जिसमें डेटा सेट की सापेक्ष आवृत्तियों का प्रतिनिधित्व किया जाता है। अर्थात्, निरपेक्ष आवृत्तियों को रेखांकन करने के बजाय, सापेक्ष आवृत्तियों को रेखांकन किया जाता है।
यद्यपि विभिन्न आवृत्तियों का प्रतिनिधित्व किया जाता है, सापेक्ष आवृत्ति हिस्टोग्राम का आकार पूर्ण आवृत्ति हिस्टोग्राम के समान होता है, वे बस ऊर्ध्वाधर अक्ष पर मान बदलते हैं।
उदाहरण के तौर पर, हम पिछले अभ्यास के सांख्यिकीय अध्ययन से सापेक्ष आवृत्ति हिस्टोग्राम का निर्माण करेंगे। ऐसा करने के लिए, हमें पहले प्रत्येक अंतराल की सापेक्ष आवृत्ति की गणना करनी होगी, जो डेटा की कुल संख्या (50) से विभाजित इसकी पूर्ण आवृत्ति के बराबर है।
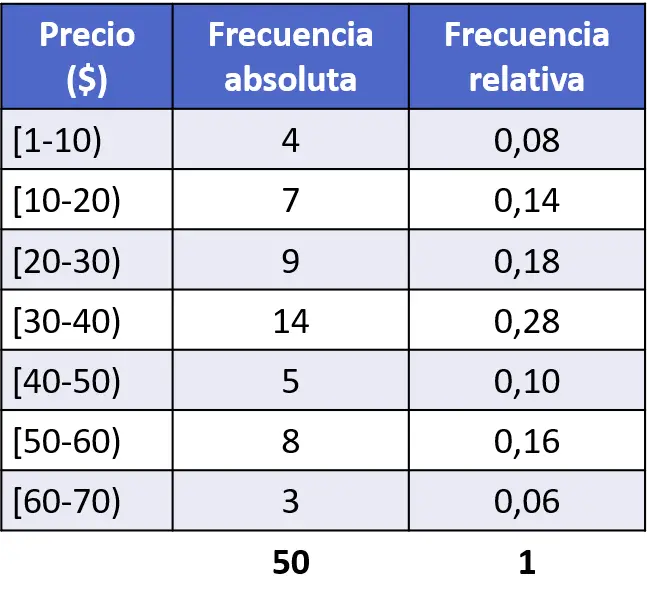
एक बार जब हम सापेक्ष आवृत्तियों की गणना कर लेते हैं, तो हम बस उन्हें हिस्टोग्राम में ग्राफ़ करते हैं। ऐसा करने के लिए, हम क्षैतिज अक्ष खींचते हैं, जो बेची गई इकाइयों की कीमतों से मेल खाती है, फिर ऊर्ध्वाधर अक्ष, जिसमें सापेक्ष आवृत्तियों का प्रतिनिधित्व किया जाता है, और अंत में, प्रत्येक अंतराल के लिए उसकी सापेक्ष आवृत्ति के बराबर ऊंचाई की एक आयताकार पट्टी खींची जाती है। . आवृत्ति।
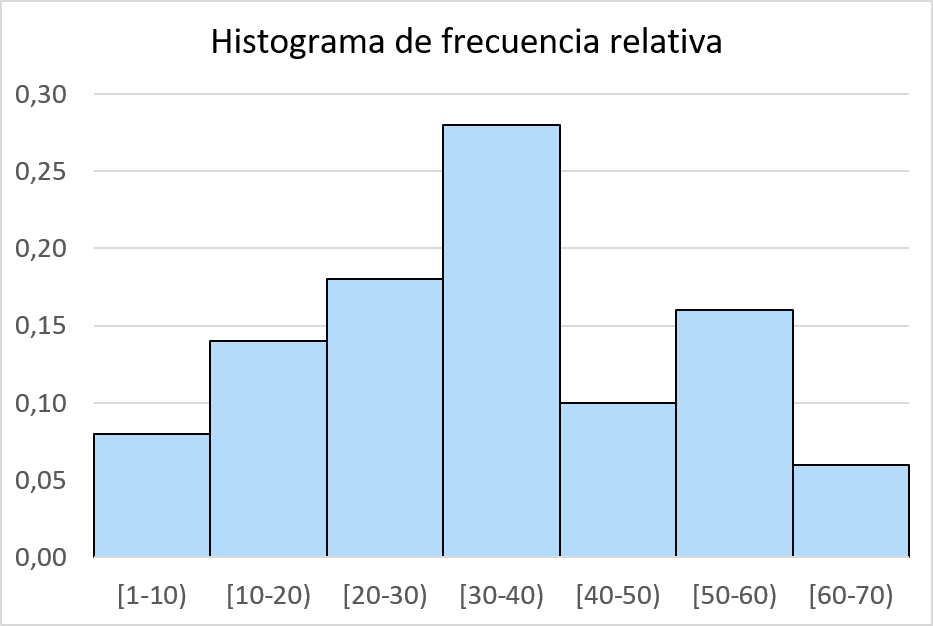
संचयी आवृत्ति हिस्टोग्राम
हमने अभी देखा कि एक निरपेक्ष आवृत्ति हिस्टोग्राम और एक सापेक्ष आवृत्ति हिस्टोग्राम का निर्माण कैसे किया जाता है, हालाँकि, संचयी आवृत्ति हिस्टोग्राम का उपयोग आंकड़ों में भी किया जाता है।
संचयी आवृत्ति हिस्टोग्राम एक प्रकार का हिस्टोग्राम है जिसमें संचयी आवृत्तियों को प्लॉट किया जाता है। अर्थात्, संचयी आवृत्ति हिस्टोग्राम में, निरपेक्ष आवृत्तियों के बजाय संचयी आवृत्तियों का प्रतिनिधित्व किया जाता है।
तार्किक रूप से, एक संचयी आवृत्ति हिस्टोग्राम निरपेक्ष और सापेक्ष आवृत्तियों के साथ बनाया जा सकता है। उदाहरण के तौर पर, इन दो प्रकार के हिस्टोग्राम को उसी डेटा का उपयोग करके नीचे दर्शाया जाएगा जैसा कि हम इस लेख में करते हैं।
संचयी निरपेक्ष आवृत्तियों का हिस्टोग्राम
जाहिर है, संचयी निरपेक्ष आवृत्तियों का हिस्टोग्राम बनाने के लिए, हमें पहले प्रत्येक अंतराल के लिए संचयी निरपेक्ष आवृत्तियों को निर्धारित करना होगा। ऐसा करने के लिए, हम प्रत्येक अंतराल पर सभी पिछली निरपेक्ष आवृत्तियों के साथ-साथ प्रश्न में अंतराल की पूर्ण आवृत्ति को जोड़ते हैं:
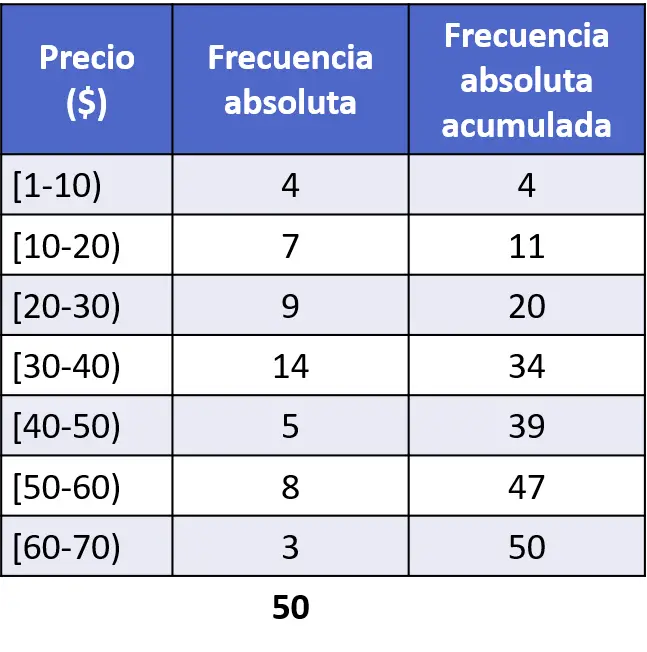
तो, अब जब हमने गणित कर लिया है, तो हम हिस्टोग्राम को प्लॉट करने के लिए बस उसी प्रक्रिया का पालन करते हैं लेकिन संचयी निरपेक्ष आवृत्तियों के साथ:
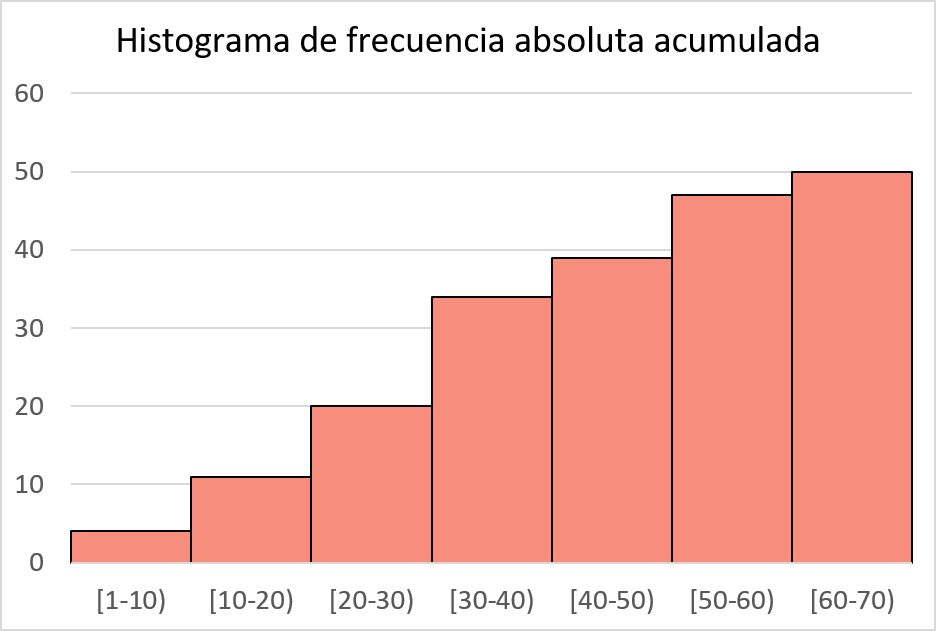
संचयी सापेक्ष आवृत्तियों का हिस्टोग्राम
संचयी सापेक्ष आवृत्तियों का हिस्टोग्राम संचयी निरपेक्ष आवृत्तियों के समान ही तैयार किया जाता है, हम पहले डेटा श्रृंखला की संचयी सापेक्ष आवृत्तियों की गणना करते हैं:
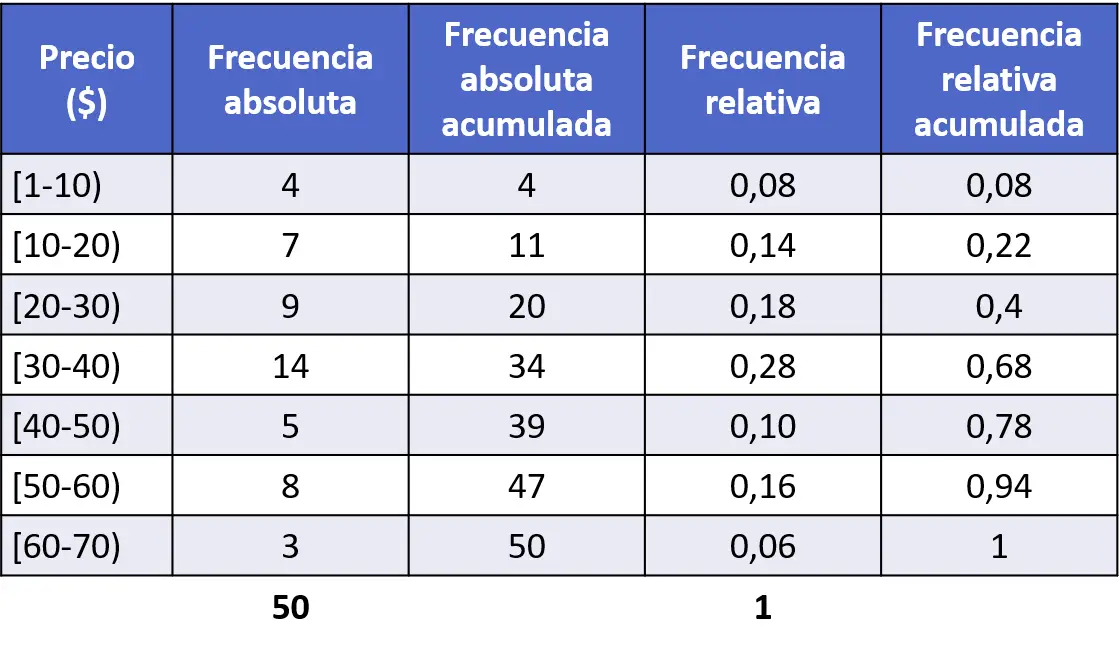
और फिर हम एक हिस्टोग्राम में संचयी सापेक्ष आवृत्ति का प्रतिनिधित्व करते हैं:
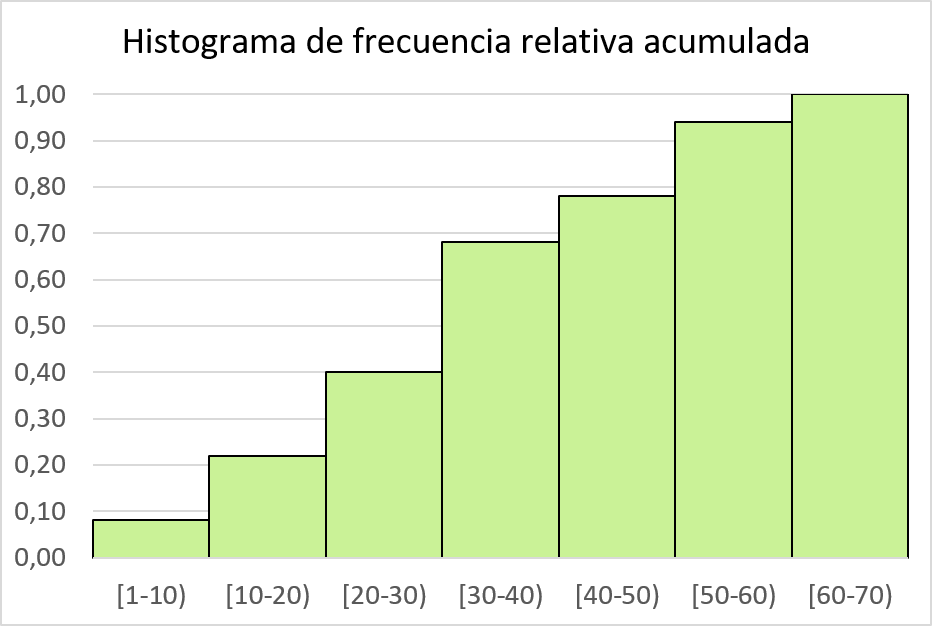
हिस्टोग्राम को आवृत्ति बहुभुज के साथ संयोजित करें
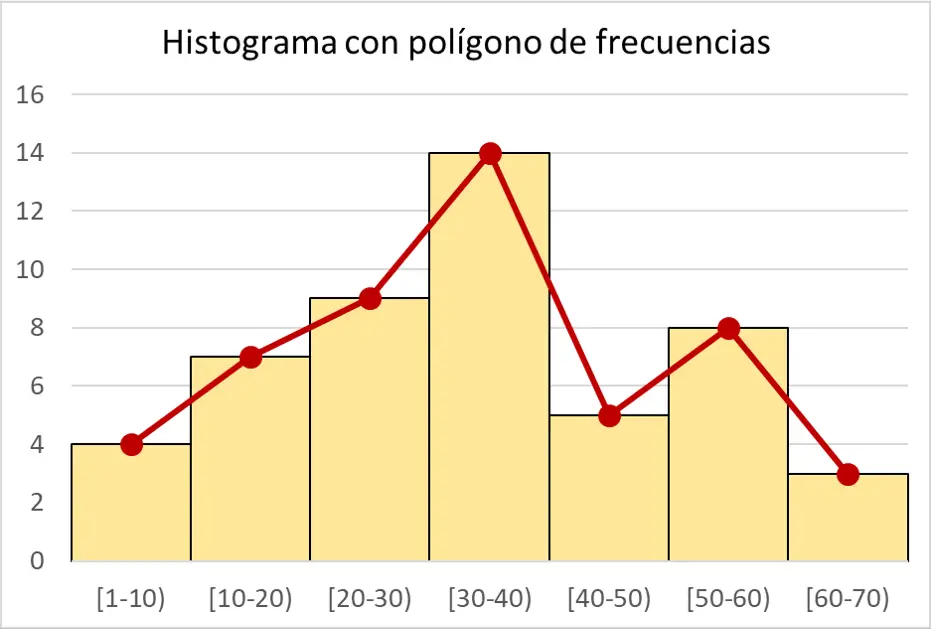
कभी-कभी आंकड़ों में हिस्टोग्राम को आवृत्ति बहुभुज के साथ जोड़ दिया जाता है, जो सीधी रेखाओं से जुड़े बिंदुओं का एक समूह होता है। इस तरह, डेटा के विकास को अधिक स्पष्ट रूप से इंगित किया जाता है, क्योंकि आवृत्ति बहुभुज की रेखा आपको डेटा श्रृंखला की प्रगति को बेहतर ढंग से देखने की अनुमति देती है।
इन दो प्रकार के सांख्यिकीय प्लॉटों को संयोजित करने के लिए, बस प्रत्येक आयताकार हिस्टोग्राम बार के शीर्ष के बीच में एक बिंदु प्लॉट करें, फिर लगातार बिंदुओं को सीधी रेखाओं से जोड़ें।
उदाहरण के लिए, आवृत्ति बहुभुज के साथ संयुक्त इस पोस्ट की शुरुआत में उत्पन्न पूर्ण आवृत्तियों का हिस्टोग्राम है:
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने