Apa itu kurva kepadatan? (penjelasan & contoh)

Kurva kepadatan adalah kurva pada grafik yang mewakili sebaran nilai dalam sekumpulan data. Ini berguna karena tiga alasan:

1. Kurva densitas memberi kita gambaran yang baik tentang “bentuk” suatu distribusi, termasuk apakah suatu distribusi mempunyai satu atau lebih “puncak” nilai frekuensi dan apakah distribusinya condong ke kiri atau tidak. atau benar. BENAR. .

2. Kurva kepadatan memungkinkan kita melihat secara visual hubungan mean dan median suatu distribusi.

3. Kurva kepadatan memungkinkan kita melihat secara visual berapa persentase pengamatan dalam kumpulan data yang berada di antara nilai-nilai yang berbeda.

Kurva kepadatan yang paling terkenal adalah kurva berbentuk lonceng yang mewakili distribusi normal .

Untuk lebih memahami kurva kepadatan, perhatikan contoh berikut.

Contoh: membuat dan menafsirkan kurva kepadatan

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan tinggi 20 tanaman berbeda (dalam inci) di lahan tertentu:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Jika kita membuat histogram sederhana untuk menampilkan frekuensi relatif setiap nilai, maka akan terlihat seperti ini:

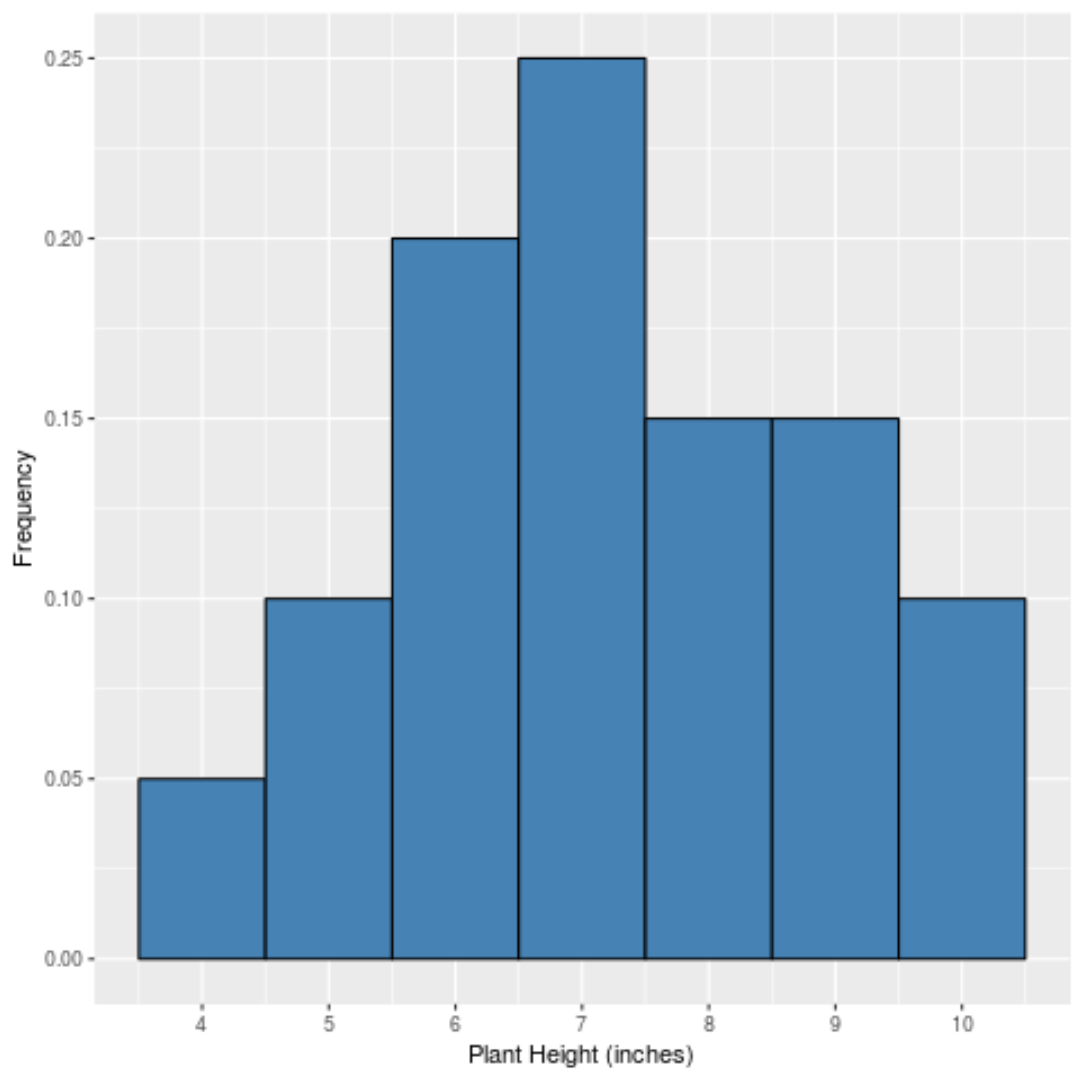
Sumbu x menunjukkan nilai data dan sumbu y menunjukkan frekuensi relatif (misalnya nilai “7” muncul 5 kali dari 20 total nilai pada dataset, sehingga memiliki frekuensi relatif 25% atau 0,25 .

Dan jika kita membuat kurva kepadatan untuk menangkap “bentuk” distribusi ini, maka akan terlihat seperti ini:

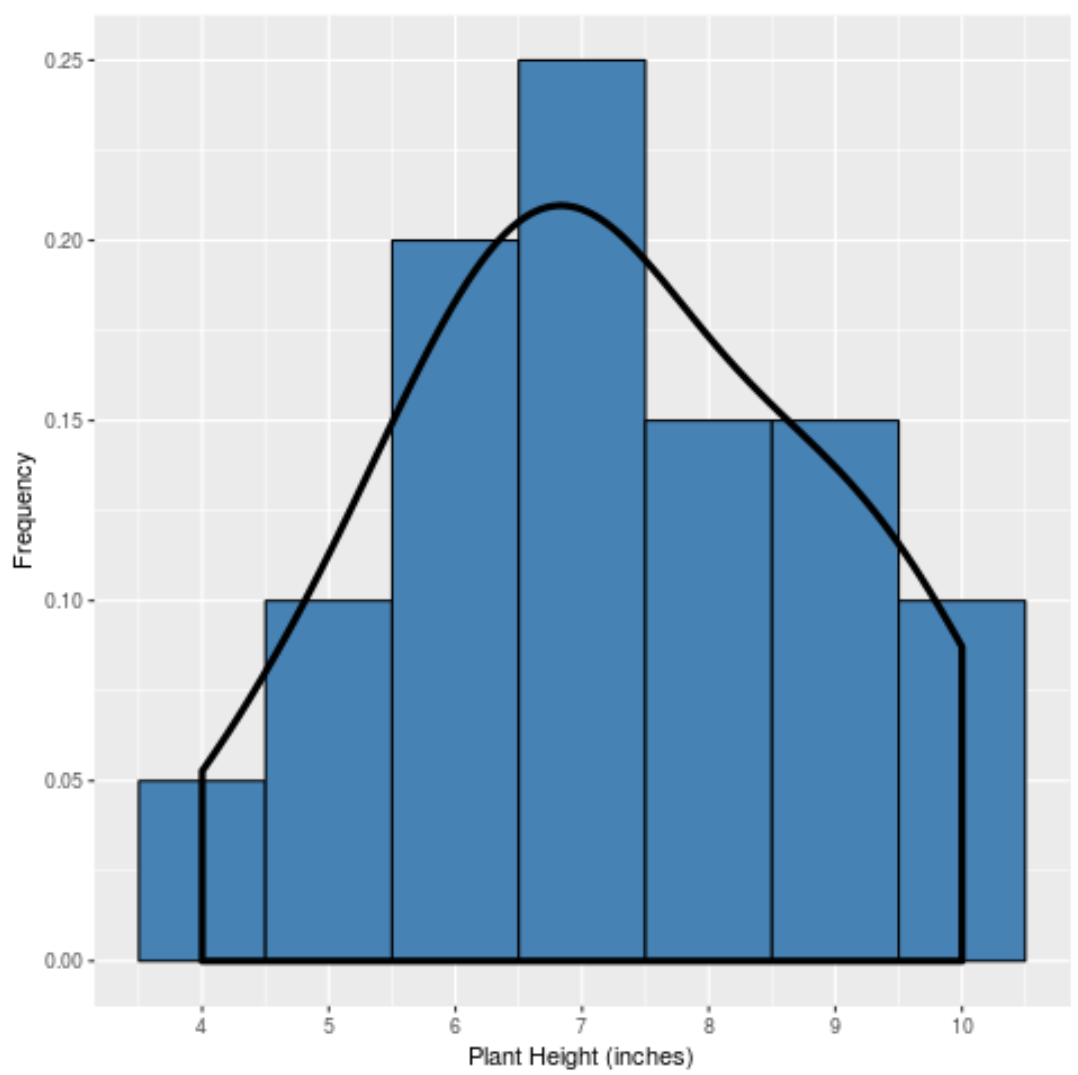
Kurva tertinggi berada di dekat pusat distribusi karena di sanalah sebagian besar nilai ditemukan. Ini juga paling rendah di dekat ujung distribusi karena lebih sedikit tanaman yang mengambil nilai ini (misalnya tinggi 4 inci atau 10 inci).

Bagaimana menafsirkan kurva kepadatan

Kurva kepadatan hadir dalam berbagai bentuk dan ukuran dan memungkinkan kita memperoleh pemahaman visual yang cepat tentang distribusi nilai dalam kumpulan data tertentu. Mereka sangat berguna untuk membantu kita memvisualisasikan:

1. Asimetri

Skewness adalah cara untuk menggambarkan simetri suatu distribusi. Kurva kepadatan memungkinkan kita melihat dengan cepat apakah suatu grafik miring ke kiri, ke kanan, atau tidak miring:

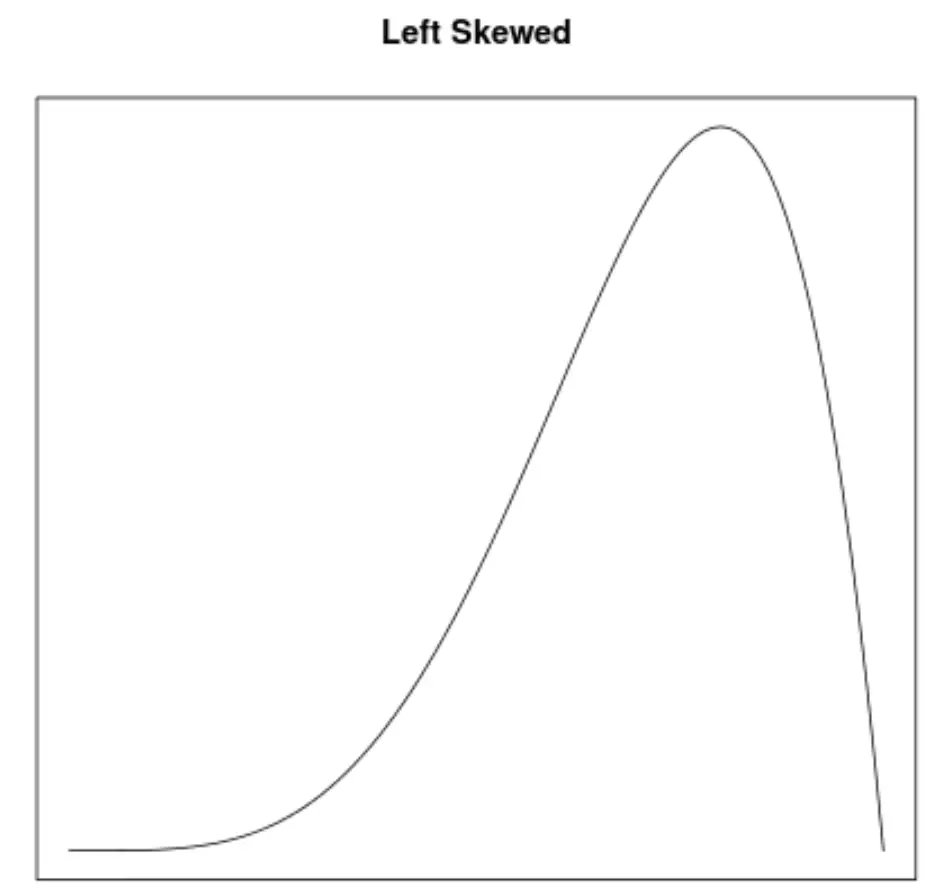
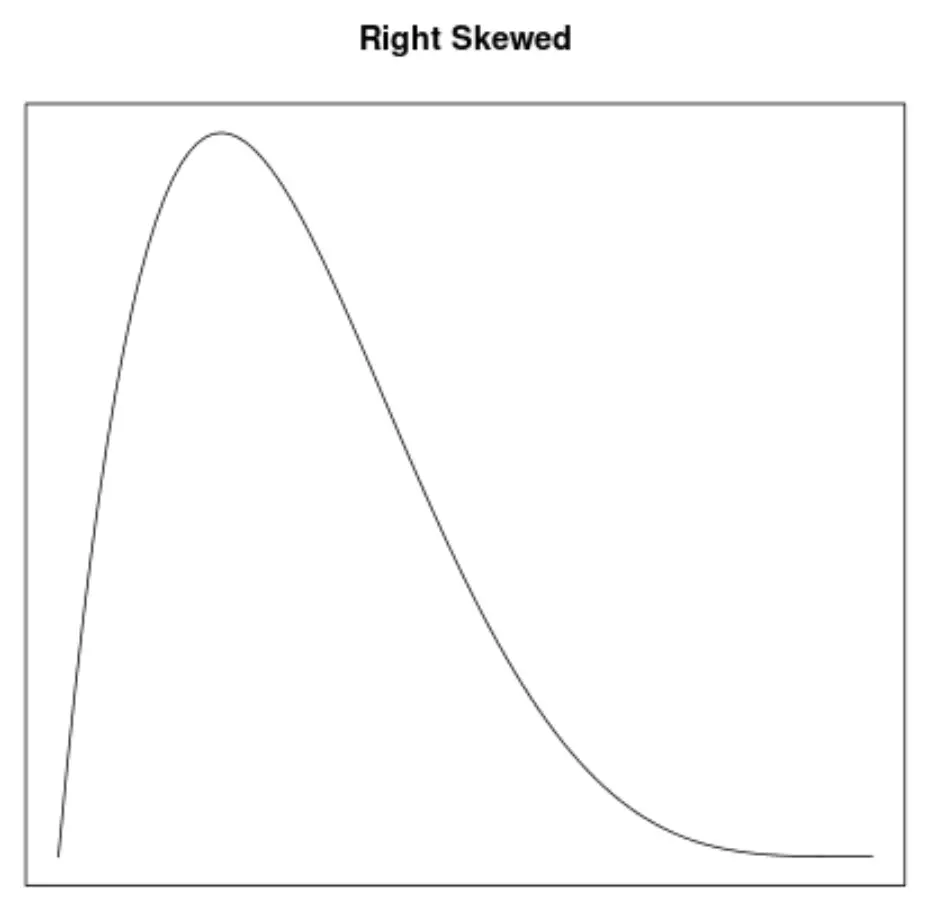
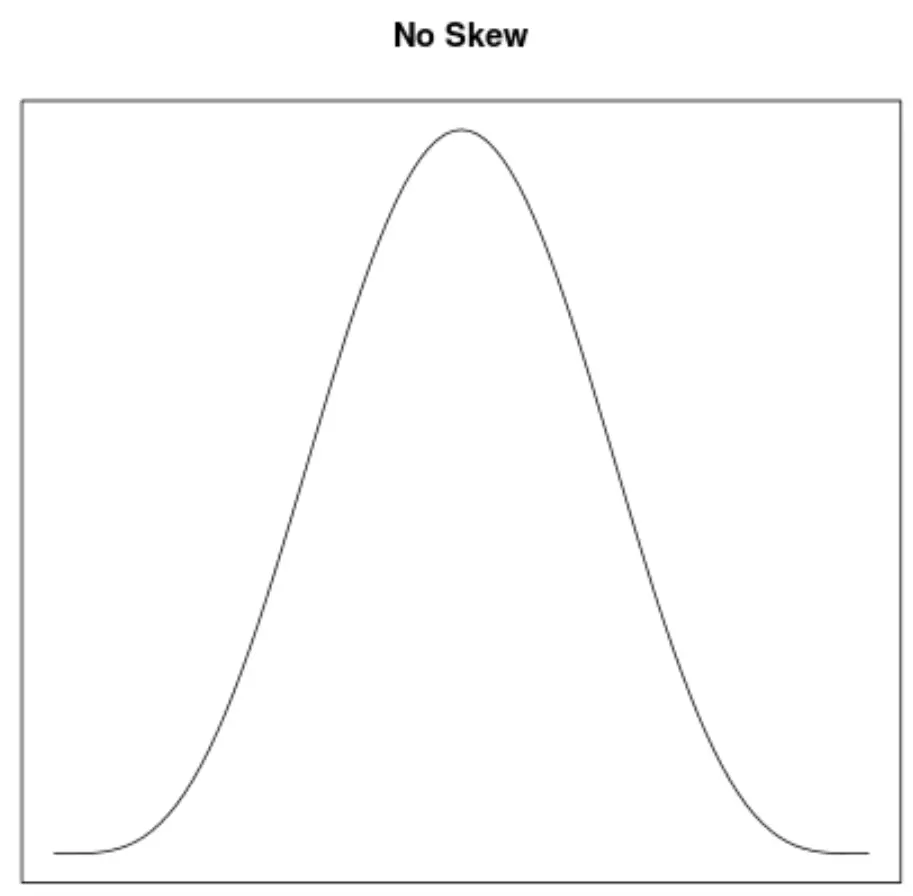
2. Letak mean dan median

Berdasarkan kemiringan kurva kepadatan, kita dapat dengan cepat mengetahui apakah mean atau median lebih besar dalam suatu distribusi tertentu. Khususnya:

• Jika kurva kepadatan tetap asimetris , maka meannya lebih rendah dari mediannya.
• Jika kurva kepadatan miring ke kanan , maka meannya lebih besar dari mediannya.
• Jika kurva kepadatan tidak memiliki asimetri , maka meannya sama dengan median.

3. Jumlah puncak

Kurva kepadatan juga memungkinkan kita melihat dengan cepat berapa banyak “puncak” yang ada dalam suatu distribusi tertentu. Dalam setiap contoh di atas, distribusi hanya memiliki satu puncak, jadi kami menggambarkan distribusi ini sebagai unimodal .

Namun, beberapa distribusi dapat memiliki dua puncak yang kita sebut distribusi bimodal . Dan dalam kasus yang jarang terjadi, kita juga dapat memiliki distribusi multimodal dengan dua puncak atau lebih.

Dengan hanya membuat kurva kepadatan untuk kumpulan data tertentu, kita dapat dengan cepat melihat berapa banyak puncak dalam distribusinya.

Sifat kurva kepadatan

Kurva kepadatan memiliki sifat-sifat berikut:

• Luas area di bawah kurva selalu berjumlah 100%.
• Kurva tidak akan pernah berada di bawah sumbu x.

Ingatlah kedua fakta ini saat membuat atau menafsirkan kurva kepadatan untuk distribusi yang berbeda.

Sumber daya tambahan

Pengantar Histogram Frekuensi Relatif
Cara Membuat Kurva Lonceng di Excel
Cara Membuat Kurva Lonceng dengan Python