Fungsi distribusi

Oleh Benjamin anderson Agustus 5, 2023 Kemungkinan 0 Komentar

Pada artikel ini Anda akan menemukan penjelasan tentang fungsi distribusi, cara menghitung nilainya, dan contoh fungsi distribusi di dunia nyata. Selain itu, Anda akan dapat melihat perbedaan antara fungsi distribusi dan fungsi kepadatan.

Apa fungsi distribusinya?

Fungsi distribusi , disebut juga fungsi distribusi kumulatif , adalah fungsi matematika yang menunjukkan probabilitas kumulatif suatu distribusi. Artinya, gambaran fungsi distribusi untuk nilai apa pun sama dengan probabilitas bahwa variabel tersebut mengambil nilai tersebut atau nilai yang lebih rendah.

Fungsi distribusi kumulatif juga dapat disebut dengan akronim FDA, meskipun simbol biasanya adalah huruf kapital F.

Oleh karena itu, fungsi distribusi ditentukan dengan rumus berikut:

$F(x)=P[X\leq x]$

Cara menghitung fungsi distribusi

Kami kemudian menjelaskan cara menghitung nilai fungsi distribusi tergantung pada apakah distribusi probabilitasnya diskrit atau kontinu.

Kotak rahasia

Jika variabel acaknya diskrit, fungsi distribusi kumulatifnya sama dengan jumlah probabilitas semua nilai yang sama dengan atau kurang dari x .

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

Emas

$f(u)$

adalah fungsi probabilitas yang terkait dengan variabel diskrit.

Kasus lanjutan

Jika variabel acak kontinu, fungsi distribusi kumulatif setara dengan integral fungsi kepadatan dari minus tak terhingga ke nilai yang dimaksud.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

Emas

$f(u)$

adalah fungsi kepadatan yang terkait dengan variabel kontinu.

Contoh Fungsi Distribusi

Sekarang setelah kita mengetahui definisi fungsi distribusi, mari kita lihat contoh praktis langkah demi langkah untuk mempelajari cara menghitung nilai fungsi distribusi.

Hitung fungsi distribusi percobaan acak pelemparan koin sebanyak empat kali.

Untuk menyelesaikan latihan ini, Anda harus terlebih dahulu menghitung semua probabilitas yang terkait dengan jumlah kepala yang diperoleh selama empat pelemparan koin:

Jadi, karena merupakan variabel diskrit, maka untuk menentukan gambaran fungsi distribusi cukup dengan menjumlahkan probabilitas hingga nilai variabel yang bersangkutan:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

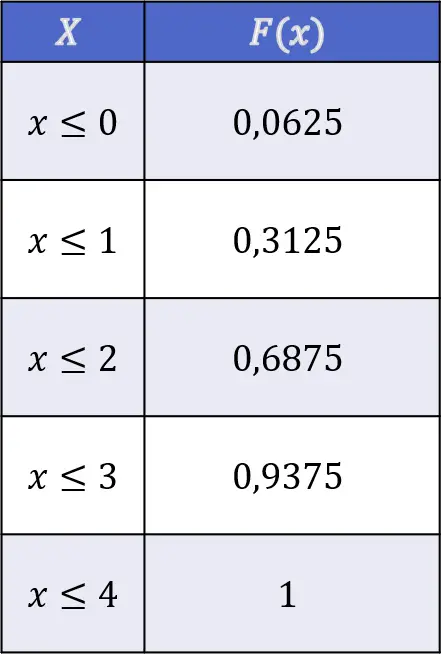
Jadi, nilai fungsi distribusi lemparan kepala dengan cara pelemparan empat buah uang logam yang saling bebas adalah sebagai berikut:

Sifat-sifat fungsi distribusi

Terlepas dari jenis variabelnya, fungsi distribusi selalu memiliki properti berikut:

Nilai fungsi distribusi kumulatif antara 0 dan 1 inklusif.

$0\leq F(x) \leq 1$

Limit suatu fungsi distribusi karena x cenderung tak terhingga sama dengan 1.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

Sebaliknya, limit fungsi distribusi ketika x mendekati minus tak terhingga adalah nol.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

Berdasarkan ciri-cirinya, fungsi distribusi bersifat monoton dan tidak menurun.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Selanjutnya jika
$a\leq b$

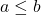
persamaan berikut terpenuhi.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Fungsi distribusi dan fungsi kepadatan

Terakhir, kita akan melihat apa perbedaan antara fungsi distribusi dan fungsi kepadatan, karena kedua pengertian statistik ini sering kali membingungkan.

Perbedaan antara fungsi distribusi dan fungsi kepadatan adalah jenis probabilitas yang ditentukannya. Fungsi kepadatan menggambarkan probabilitas suatu variabel memperoleh nilai tertentu, sedangkan fungsi distribusi menggambarkan probabilitas kumulatif variabel tersebut.

Artinya, fungsi distribusi digunakan untuk menghitung probabilitas suatu variabel sama dengan atau kurang dari nilai tertentu.

Perhatikan bahwa fungsi kepadatan hanya mengacu pada variabel kontinu, jadi perbedaan ini hanya masuk akal jika variabel yang diteliti adalah variabel kontinu.

Perhatikan bagaimana representasi grafis dari fungsi distribusi berubah dibandingkan dengan fungsi kepadatan suatu variabel yang mengikuti distribusi normal dengan rata-rata 1 dan deviasi standar 0,5:

perbedaan antara fungsi distribusi dan fungsi kepadatan

Untuk mempelajari lebih lanjut tentang fungsi kepadatan, lihat artikel berikut:

➤ Lihat: fungsi kepadatan

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya