Bagaimana melakukan uji-t welch di r

Uji-t Welch digunakan untuk membandingkan mean antara dua kelompok independen jika kedua kelompok tidak diasumsikan memiliki varian yang sama.

Untuk melakukan uji-t Welch di R, kita dapat menggunakan fungsi t.test() , yang menggunakan sintaks berikut:

t.test(x, y, alternatif = c(“dua muka”, “kurang”, “lebih besar”))

Emas:

• x : vektor numerik dari nilai data untuk kelompok pertama
• y : vektor numerik dari nilai data untuk kelompok kedua
• alternatif: hipotesis alternatif untuk pengujian. Standarnya adalah dua sisi.

Contoh berikut menunjukkan cara menggunakan fungsi ini untuk melakukan uji-t Welch di R.

Contoh: Uji-t Welch di R

Seorang guru ingin membandingkan hasil ujian dari 12 siswa yang menggunakan buku persiapan ujian untuk mempersiapkan ujian versus 12 siswa yang tidak.

Berikut vektor yang menunjukkan hasil ujian siswa pada masing-masing kelompok:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Sebelum melakukan uji-t Welch, kita dapat membuat diagram kotak terlebih dahulu untuk memvisualisasikan distribusi skor untuk setiap kelompok:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

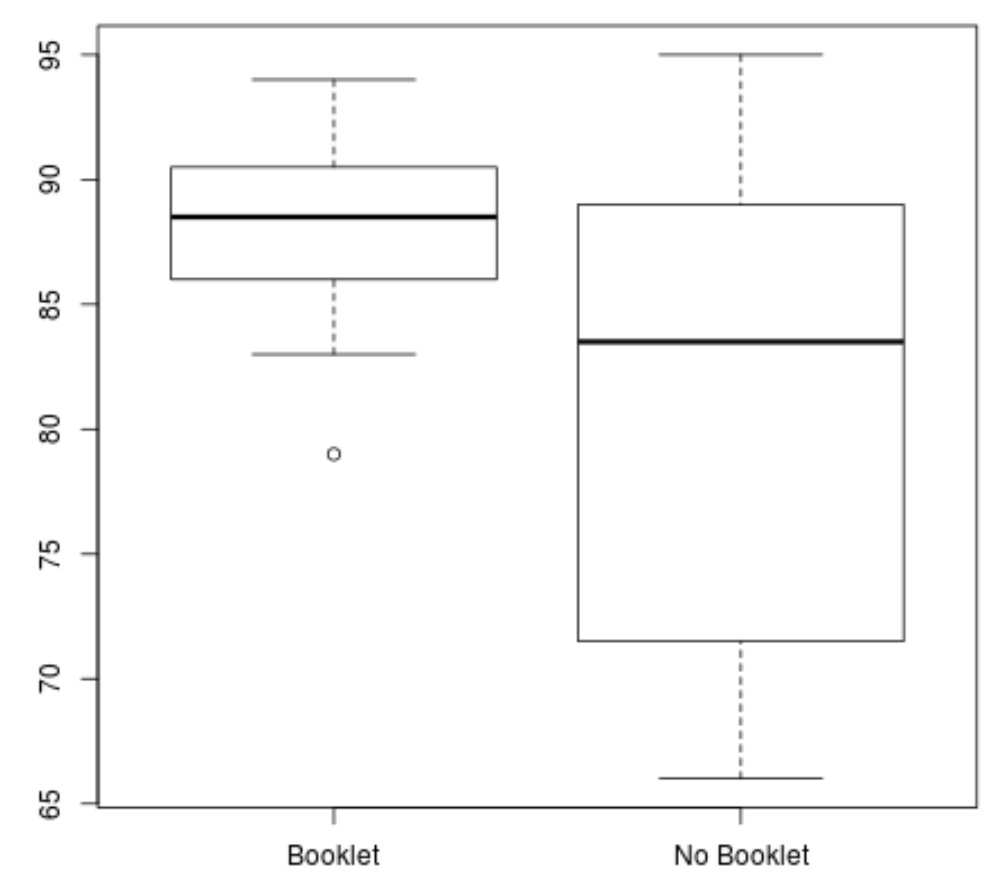
Kita dapat melihat dengan jelas bahwa kelompok “Buklet” mempunyai skor rata-rata lebih tinggi dan varians skor lebih rendah.

Untuk menguji secara formal apakah skor rata-rata antar kelompok berbeda secara signifikan, kita dapat melakukan uji-t Welch:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

Dari hasilnya, kita dapat melihat bahwa statistik uji- t adalah 2,2361 dan nilai p yang sesuai adalah 0,04171 .

Karena nilai p ini kurang dari 0,05, kita dapat menolak hipotesis nol dan menyimpulkan bahwa terdapat perbedaan yang signifikan secara statistik dalam nilai rata-rata ujian antara kedua kelompok.

Fungsi t.test() juga memberi kita informasi berikut:

• Interval kepercayaan 95% untuk perbedaan nilai rata-rata ujian antara kedua kelompok adalah [0,3048, 13,8618 ].
• Rata-rata nilai ujian kelompok pertama adalah 87,91667 .
• Rata-rata nilai ujian kelompok kedua adalah 80,83333 .

Anda dapat menemukan dokumentasi lengkap untuk fungsi t.test() di sini .

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara melakukan uji-t satu sampel di R
Cara melakukan uji-t dua sampel di R
Cara melakukan uji-t sampel berpasangan di R
Cara memplot beberapa plot kotak dalam satu grafik di R