Cara menghitung skewness & kurtosis di r

Dalam statistik, skewness dan kurtosis adalah dua cara untuk mengukur bentuk suatu distribusi.

Skewness adalah ukuran kemiringan suatu distribusi. Nilai ini bisa positif atau negatif.

• Kemiringan negatif menunjukkan bahwa ekornya berada di sisi kiri distribusi, yang mengarah ke nilai yang lebih negatif.
• Kemiringan positif menunjukkan bahwa ekornya berada di sisi kanan distribusi, yang mengarah ke nilai yang lebih positif.
• Nilai nol menunjukkan tidak adanya asimetri dalam distribusi, artinya distribusi tersebut simetris sempurna.

Kurtosis merupakan ukuran apakah suatu distribusi tergolong berat atau ringan dibandingkan dengan distribusi normal .

• Kurtosis berdistribusi normal adalah 3.
• Jika suatu distribusi mempunyai kurtosis kurang dari 3, maka dikatakan playkurtic , artinya distribusi tersebut cenderung menghasilkan outlier yang lebih sedikit dan tidak ekstrim dibandingkan distribusi normal.
• Jika suatu distribusi mempunyai kurtosis lebih besar dari 3 maka dikatakan leptokurtik , artinya cenderung menghasilkan lebih banyak outlier dibandingkan distribusi normal.

Catatan: Beberapa rumus (definisi Fisher) mengurangkan 3 dari kurtosis agar lebih mudah dibandingkan dengan distribusi normal. Dengan menggunakan definisi ini, suatu distribusi akan memiliki kurtosis yang lebih besar daripada distribusi normal jika nilai kurtosisnya lebih besar dari 0.

Tutorial ini menjelaskan cara menghitung skewness dan kurtosis dari kumpulan data tertentu di R.

Contoh: Skewness dan Flattening di R

Misalkan kita memiliki kumpulan data berikut:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Kita dapat dengan cepat memvisualisasikan distribusi nilai dalam kumpulan data ini dengan membuat histogram:

 hist(data, col=' steelblue ') 

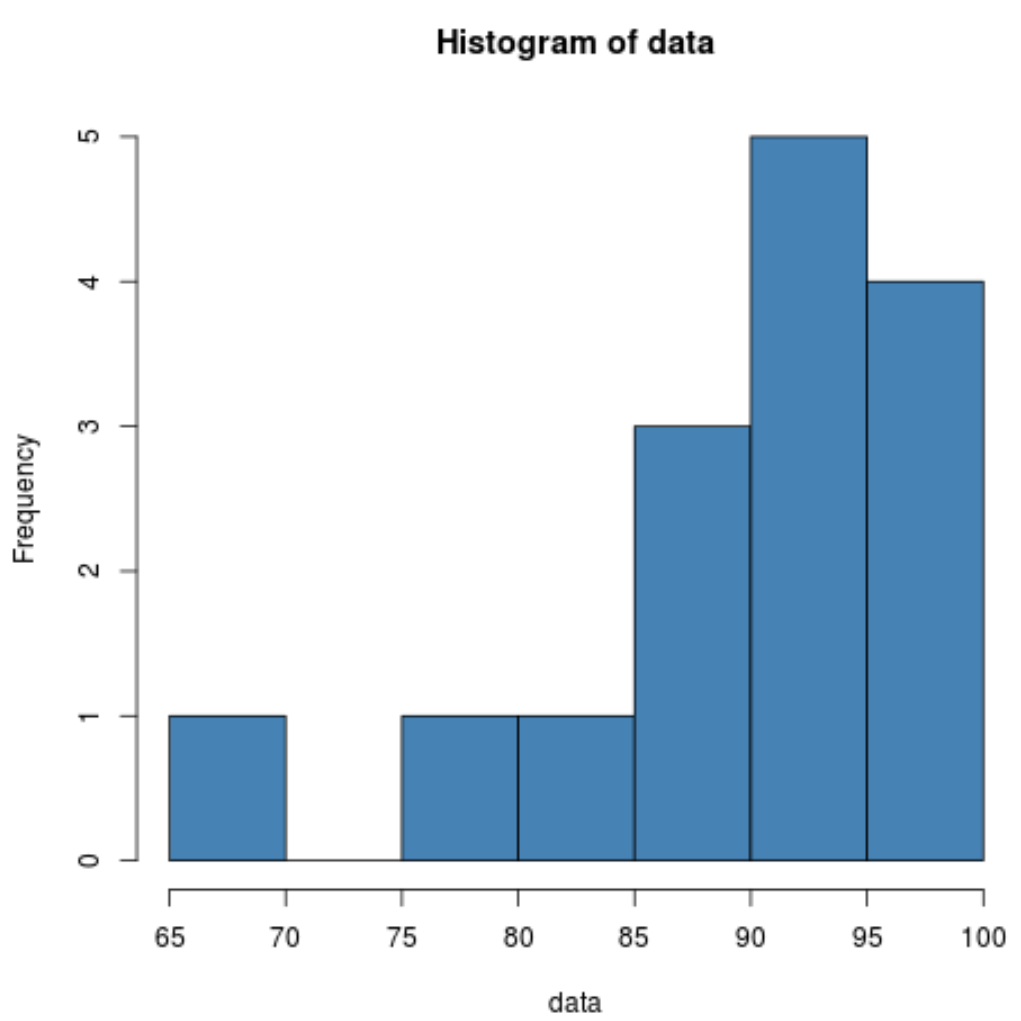
Histogram menunjukkan kepada kita bahwa distribusinya tampak condong ke kiri. Artinya, sebagian besar nilai terkonsentrasi di sisi kanan distribusi.

Untuk menghitung skewness dan kurtosis dari dataset ini, kita dapat menggunakan fungsi skewness() dan kurtosis() dari perpustakaan momen di R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Skewnessnya ternyata -1.391777 dan kurtosisnya jadi 4.177865 .

Karena kemiringannya negatif, hal ini menunjukkan bahwa distribusinya miring ke kiri. Ini menegaskan apa yang kita lihat di histogram.

Karena kurtosisnya lebih besar dari 3, hal ini menunjukkan bahwa distribusi tersebut memiliki nilai yang lebih banyak di bagian ekor dibandingkan dengan distribusi normal.

Pustaka momen juga menawarkan fungsi jarque.test() , yang melakukan uji kesesuaian yang menentukan apakah data sampel menunjukkan kemiringan dan kurtosis yang konsisten dengan distribusi normal. Hipotesis nol dan alternatif dari pengujian ini adalah sebagai berikut:

Hipotesis nol : Kumpulan data memiliki skewness dan kurtosis yang sesuai dengan distribusi normal.

Hipotesis alternatif : Dataset memiliki kemiringan dan kurtosis yang tidak sesuai dengan distribusi normal.

Kode berikut menunjukkan cara melakukan tes ini:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

Nilai p dari tes tersebut ternyata 0,05756 . Karena nilai ini tidak kurang dari α = 0,05, kita gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa kumpulan data ini memiliki skewness dan kurtosis yang berbeda dari distribusi normal.

Anda dapat menemukan dokumentasi lengkap Moments Library di sini .

Bonus: kalkulator kemiringan dan kurtosis

Anda juga dapat menghitung kemiringan untuk kumpulan data tertentu menggunakan Kalkulator Skewness dan Kurtosis Statistik , yang secara otomatis menghitung kemiringan dan kurtosis untuk kumpulan data tertentu.