Apa yang dimaksud dengan overfitting dalam pembelajaran mesin? (penjelasan & contoh)

Dalam pembelajaran mesin, kita sering kali membuat model sehingga kita dapat membuat prediksi akurat tentang fenomena tertentu.

Misalnya, kita ingin membuat model regresi yang menggunakan variabel prediktor jam belajar untuk memprediksi skor ACT variabel respon untuk siswa sekolah menengah.

Untuk membangun model ini, kami akan mengumpulkan data tentang jumlah jam belajar dan skor ACT yang sesuai untuk ratusan siswa di distrik sekolah tertentu.

Kami kemudian akan menggunakan data ini untuk melatih model yang dapat membuat prediksi tentang skor yang akan diterima siswa berdasarkan jumlah jam belajar.

Untuk menilai kegunaan model, kita dapat mengukur seberapa cocok prediksi model dengan data observasi. Salah satu metrik yang paling umum digunakan untuk melakukan hal ini adalah mean square error (MSE), yang dihitung sebagai berikut:

MSE = (1/n)*Σ(y _saya – f(x _saya )) ²

Emas:

• n: jumlah total observasi
• y _i : Nilai respon observasi ^ke-i
• f(x _i ) : Nilai respon prediksi observasi ^ke -i

Semakin dekat prediksi model dengan observasi, maka MSE akan semakin rendah.

Namun, salah satu kesalahan terbesar yang dilakukan dalam pembelajaran mesin adalah mengoptimalkan model untuk mengurangi MSE pelatihan , yaitu seberapa cocok prediksi model dengan data yang kami gunakan untuk melatih model.

Ketika sebuah model terlalu berfokus pada pengurangan UMK pelatihan, sering kali model tersebut bekerja terlalu keras untuk menemukan pola dalam data pelatihan yang hanya disebabkan oleh kebetulan. Kemudian, ketika model diterapkan pada data yang tidak terlihat, performanya buruk.

Fenomena ini dikenal dengan istilah overfitting . Hal ini terjadi ketika kita “menyesuaikan” model terlalu dekat dengan data pelatihan sehingga akhirnya membuat model yang tidak berguna untuk membuat prediksi pada data baru.

Contoh overfitting

Untuk memahami overfitting, mari kembali ke contoh pembuatan model regresi yang menggunakan waktu belajar yang dihabiskan untuk memprediksi skor ACT .

Katakanlah kita mengumpulkan data untuk 100 siswa di distrik sekolah tertentu dan membuat diagram sebar cepat untuk memvisualisasikan hubungan antara dua variabel:

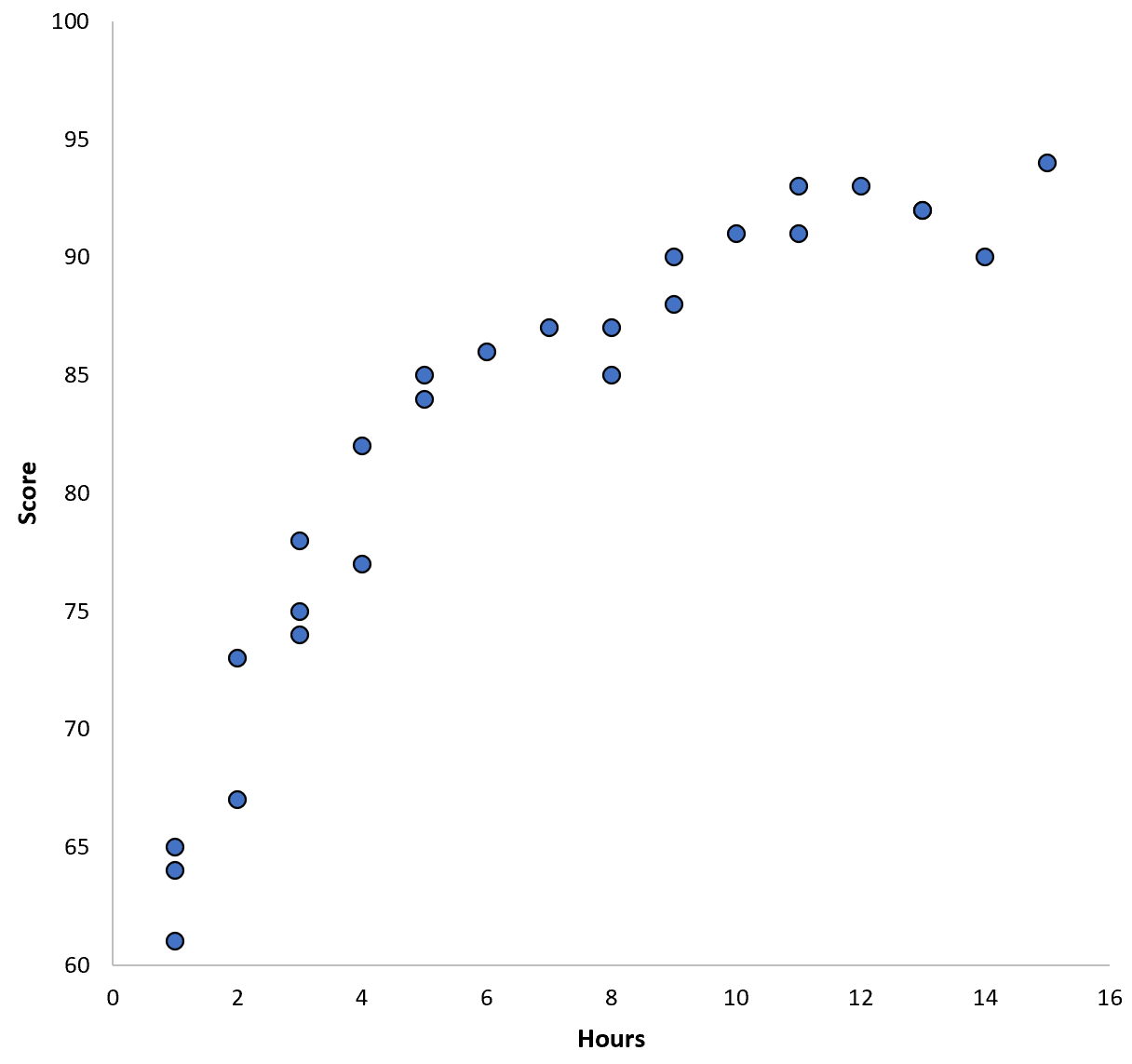
Hubungan antara kedua variabel tampak bersifat kuadrat, jadi misalkan kita menerapkan model regresi kuadrat berikut:

Skor = 60,1 + 5,4*(Jam) – 0,2*(Jam) ²

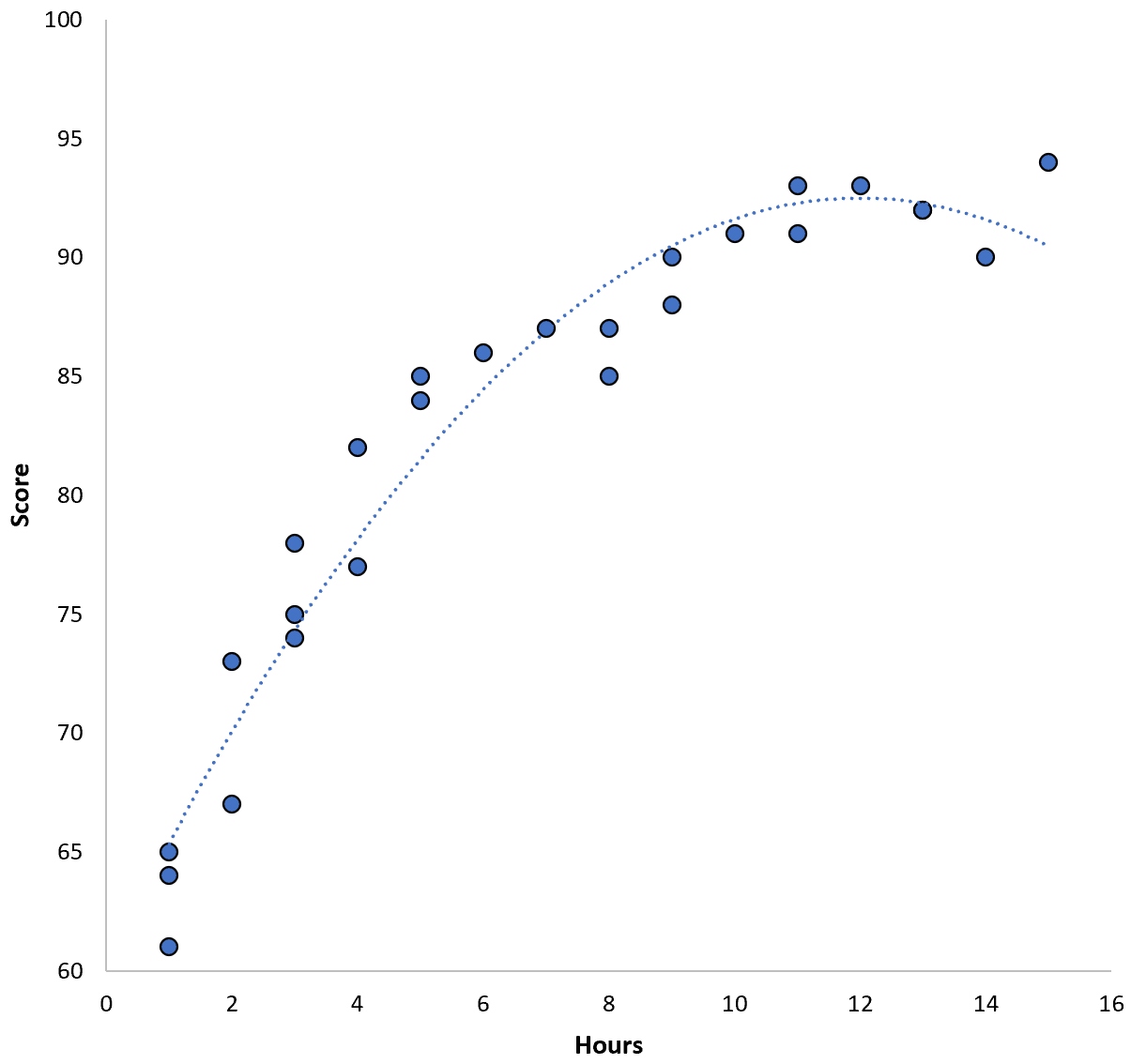
Model ini memiliki mean square error pelatihan (MSE) sebesar 3,45 . Artinya, selisih akar rata-rata kuadrat antara prediksi yang dibuat model dan skor ACT sebenarnya adalah 3,45.

Namun, kita dapat mengurangi UMK pelatihan ini dengan memasang model polinomial tingkat tinggi. Misalnya kita menerapkan model berikut:

Skor = 64,3 – 7,1*(Jam) + 8,1*(Jam) ² – 2,1*(Jam) ³ + 0,2*(Jam ^{) 4 – 0,1*(Jam) 5 +} 0,2(Jam) ⁶

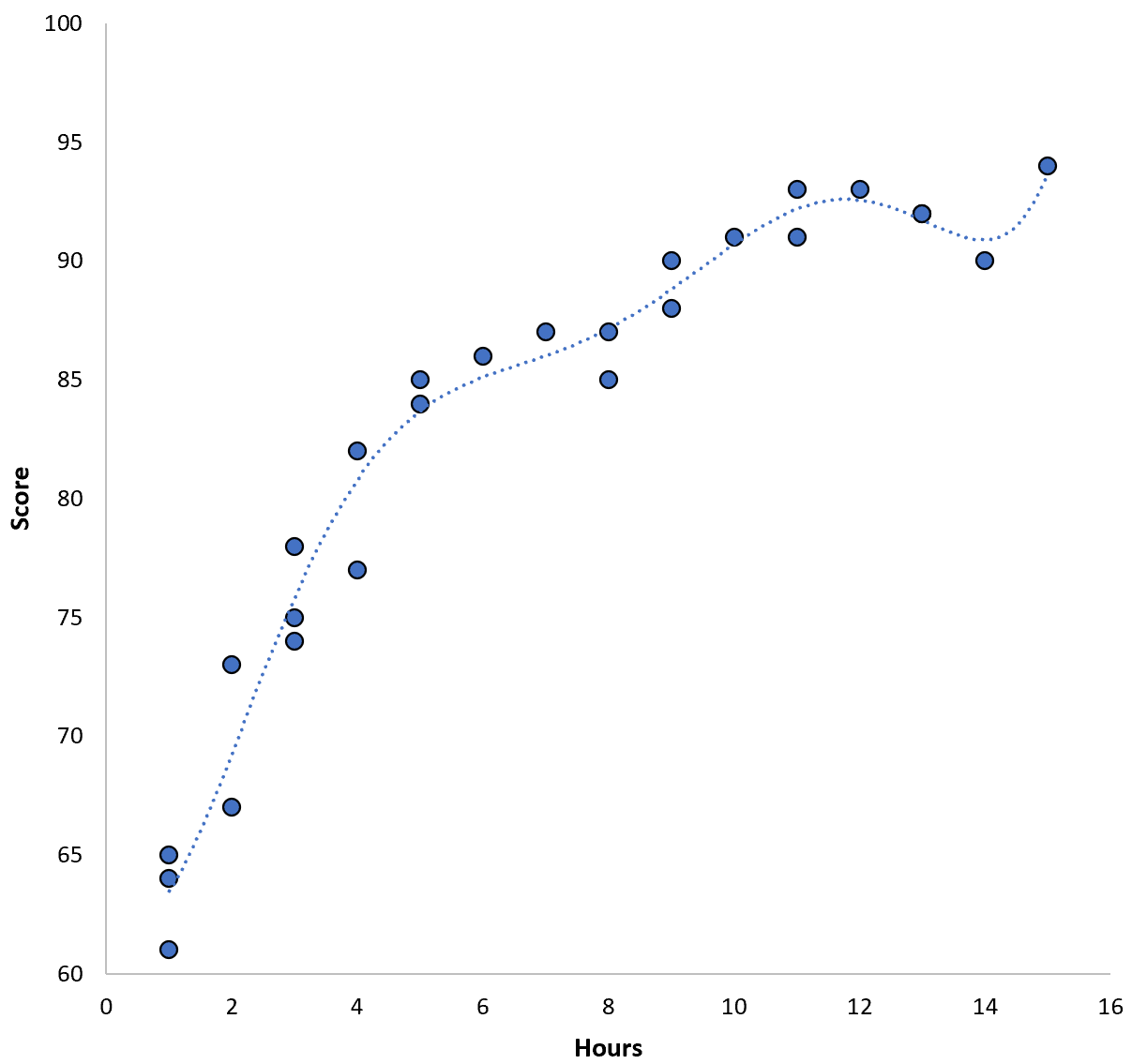
Perhatikan bagaimana garis regresi lebih cocok dengan data sebenarnya dibandingkan garis regresi sebelumnya.

Model ini memiliki root mean square error (MSE) pelatihan hanya sebesar 0,89 . Artinya, selisih akar rata-rata kuadrat antara prediksi yang dibuat model dan skor ACT sebenarnya adalah 0,89.

Pelatihan UMK ini jauh lebih kecil dibandingkan dengan model sebelumnya.

Namun, kami tidak terlalu peduli dengan UMK pelatihan , yaitu seberapa cocok prediksi model dengan data yang kami gunakan untuk melatih model. Sebaliknya, kami lebih mementingkan pengujian MSE – yaitu pengujian MSE ketika model kami diterapkan pada data yang tidak terlihat.

Jika kita menerapkan model regresi polinomial tingkat tinggi di atas pada kumpulan data yang tidak terlihat, kemungkinan besar kinerjanya akan lebih buruk daripada model regresi kuadrat yang lebih sederhana. Artinya, hal ini akan menghasilkan tes MSE yang lebih tinggi, dan hal ini sebenarnya tidak kita inginkan.

Cara mendeteksi dan menghindari overfitting

Cara paling sederhana untuk mendeteksi overfitting adalah dengan melakukan validasi silang. Metode yang paling umum digunakan dikenal sebagai k-fold cross-validation dan cara kerjanya sebagai berikut:

Langkah 1: Bagi kumpulan data secara acak menjadi k kelompok, atau “lipatan”, dengan ukuran yang kira-kira sama.

Langkah 2: Pilih salah satu lipatan sebagai set pegangan Anda. Sesuaikan template dengan sisa k-1 lipatan. Hitung uji MSE pada pengamatan pada lapisan yang dikencangkan.

Langkah 3: Ulangi proses ini sebanyak k kali, setiap kali menggunakan himpunan berbeda sebagai himpunan pengecualian.

Langkah 4: Hitung keseluruhan UMK tes sebagai rata-rata dari k UMK tes tersebut.

Uji MSE = (1/k)*ΣMSE _i

Emas:

• k : Jumlah lipatan
• MSE _i : Menguji MSE pada iterasi ^ke-i

Tes MSE ini memberi kita gambaran bagus tentang bagaimana kinerja model tertentu pada data yang tidak diketahui.

Dalam praktiknya, kami dapat menyesuaikan beberapa model berbeda dan melakukan validasi silang k-fold pada setiap model untuk mengetahui uji MSE-nya. Kita kemudian dapat memilih model dengan uji MSE terendah sebagai model terbaik untuk digunakan dalam membuat prediksi di masa mendatang.

Hal ini memastikan bahwa kami memilih model yang kemungkinan memiliki performa terbaik pada data masa depan, dibandingkan dengan model yang hanya meminimalkan UMK pelatihan dan “cocok” dengan data historis.

Sumber daya tambahan

Apa yang dimaksud dengan tradeoff bias-varians dalam pembelajaran mesin?
Pengantar Validasi Silang K-Fold
Model regresi dan klasifikasi dalam pembelajaran mesin